problem
stringlengths 5
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 4
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 5
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 10k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
There is a population $P$ of 10000 bacteria, some of which are friends (friendship is mutual), so that each bacterion has at least one friend and if we wish to assign to each bacterion a coloured membrane so that no two friends have the same colour, then there is a way to do it with 2021 colours, but not with 2020 or less.
Two friends $A$ and $B$ can decide to merge in which case they become a single bacterion whose friends are precisely the union of friends of $A$ and $B$. (Merging is not allowed if $A$ and $B$ are not friends.) It turns out that no matter how we perform one merge or two consecutive merges, in the resulting population it would be possible to assign 2020 colours or less so that no two friends have the same colour. Is it true that in any such population $P$ every bacterium has at least 2021 friends?
## Proposed by Bulgaria
|
1. The answer is affirmative.
We will use the terminology of graph theory. Here the vertices of our main graph $G$ are the bacteria and there is an edge between two precisely when they are friends. The degree $d(v)$ of a vertex $v$ of $G$ is the number of neighbours of $v$. The minimum degree $\delta(G)$ of $G$ is the smallest amongst all $d(v)$ for vertices $v$ of $G$. The chromatic number $\chi(G)$ of $G$ is the number of colours needed in order to colour the vertices such that neighbouring vertices get distinct colours.
It suffices to establish the following:
Claim. Let $k$ be a positive integer and let $G$ be a graph on $n>k$ vertices with $\delta(G) \geqslant 1$ and $\chi(G)=k$. Suppose that merging one pair or two pairs of vertices results in a graph $G^{\prime}$ with $\chi\left(G^{\prime}\right) \leqslant k-1$. Then $\delta(G) \geqslant k$.
We establish this in a series of claims.
Claim 1. $\delta(G) \geqslant k-1$.
Proof. Suppose for contradiction that we have a vertex $v$ of degree $r \leqslant k-2$ and denote its neighbours by $v_{1}, \ldots, v_{r}$. (Note that, by assumption, $v$ has at least one neighbour.)
Suppose we merge $v$ with $v_{i}$. We denote the new vertex by $v_{0}$, and we colour the obtained graph in $k-1$ colours. Note that at most $r \leqslant k-2$ colours can appear in the set $S_{1}=$ $\left\{v_{0}, v_{1}, \ldots, v_{i-1}, v_{i+1}, \ldots, v_{r}\right\}$. Therefore we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
So from now on we may assume that there is a vertex $v$ of $G$ with $\operatorname{deg}(v)=k-1$, as otherwise the proof is complete. We denote its neighbours by $v_{1}, \ldots, v_{k-1}$.
Claim 2. The set of neighbours of $v$ induces a complete graph.
Proof of Claim 2. Suppose $v_{i} v_{j} \notin E(G)$. Merge $v$ with $v_{i}$, giving a next vertex $w$, and then merge $w$ with $v_{j}$, denoting the newest vertex by $v_{0}$. Then colour the resulting graph in $k-1$ colours. Note that at most $k-2$ colours can appear in the set $S_{2}=\left\{v_{0}, v_{1}, \ldots, v_{k-1}\right\} \backslash\left\{v_{i}, v_{j}\right\}$. So we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and $v_{j}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
Claim 3. For every edge $u w$, both $u$ and $w$ belong in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$.
Proof. Otherwise merge $u$ and $w$ and call the new vertex $z$. If $u, w \notin\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ then by Claim 2 the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ and so its chromatic number is at least $k$, a contradiction. If one of $u, w$ belongs in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$, say
$u=v_{i}$, then the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}, z\right\} \backslash\left\{v_{i}\right\}$. This is again a contradiction.
From Claim 3 we see that $G$ consists of a complete set on $k$ vertices together with $n-k>0$ isolated vertices. This is a contradiction as $\delta(G) \geqslant 1$.
Remark. We do not know if the result is best possible or whether it can be improved to show $\delta(G) \geqslant 2022$.
## GEOMETRY
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a population $P$ of 10000 bacteria, some of which are friends (friendship is mutual), so that each bacterion has at least one friend and if we wish to assign to each bacterion a coloured membrane so that no two friends have the same colour, then there is a way to do it with 2021 colours, but not with 2020 or less.
Two friends $A$ and $B$ can decide to merge in which case they become a single bacterion whose friends are precisely the union of friends of $A$ and $B$. (Merging is not allowed if $A$ and $B$ are not friends.) It turns out that no matter how we perform one merge or two consecutive merges, in the resulting population it would be possible to assign 2020 colours or less so that no two friends have the same colour. Is it true that in any such population $P$ every bacterium has at least 2021 friends?
## Proposed by Bulgaria
|
1. The answer is affirmative.
We will use the terminology of graph theory. Here the vertices of our main graph $G$ are the bacteria and there is an edge between two precisely when they are friends. The degree $d(v)$ of a vertex $v$ of $G$ is the number of neighbours of $v$. The minimum degree $\delta(G)$ of $G$ is the smallest amongst all $d(v)$ for vertices $v$ of $G$. The chromatic number $\chi(G)$ of $G$ is the number of colours needed in order to colour the vertices such that neighbouring vertices get distinct colours.
It suffices to establish the following:
Claim. Let $k$ be a positive integer and let $G$ be a graph on $n>k$ vertices with $\delta(G) \geqslant 1$ and $\chi(G)=k$. Suppose that merging one pair or two pairs of vertices results in a graph $G^{\prime}$ with $\chi\left(G^{\prime}\right) \leqslant k-1$. Then $\delta(G) \geqslant k$.
We establish this in a series of claims.
Claim 1. $\delta(G) \geqslant k-1$.
Proof. Suppose for contradiction that we have a vertex $v$ of degree $r \leqslant k-2$ and denote its neighbours by $v_{1}, \ldots, v_{r}$. (Note that, by assumption, $v$ has at least one neighbour.)
Suppose we merge $v$ with $v_{i}$. We denote the new vertex by $v_{0}$, and we colour the obtained graph in $k-1$ colours. Note that at most $r \leqslant k-2$ colours can appear in the set $S_{1}=$ $\left\{v_{0}, v_{1}, \ldots, v_{i-1}, v_{i+1}, \ldots, v_{r}\right\}$. Therefore we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
So from now on we may assume that there is a vertex $v$ of $G$ with $\operatorname{deg}(v)=k-1$, as otherwise the proof is complete. We denote its neighbours by $v_{1}, \ldots, v_{k-1}$.
Claim 2. The set of neighbours of $v$ induces a complete graph.
Proof of Claim 2. Suppose $v_{i} v_{j} \notin E(G)$. Merge $v$ with $v_{i}$, giving a next vertex $w$, and then merge $w$ with $v_{j}$, denoting the newest vertex by $v_{0}$. Then colour the resulting graph in $k-1$ colours. Note that at most $k-2$ colours can appear in the set $S_{2}=\left\{v_{0}, v_{1}, \ldots, v_{k-1}\right\} \backslash\left\{v_{i}, v_{j}\right\}$. So we can get a $(k-1)$-colouring of $G$ by assigning the colour of $v_{0}$ to $v_{i}$ and $v_{j}$ and an unused colour (from the $k-1$ available) to $v$, thus contradicting the assumption that $\chi(G)=k$.
Claim 3. For every edge $u w$, both $u$ and $w$ belong in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$.
Proof. Otherwise merge $u$ and $w$ and call the new vertex $z$. If $u, w \notin\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ then by Claim 2 the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$ and so its chromatic number is at least $k$, a contradiction. If one of $u, w$ belongs in the set $\left\{v, v_{1}, \ldots, v_{k-1}\right\}$, say
$u=v_{i}$, then the resulting graph contains a complete graph on $\left\{v, v_{1}, \ldots, v_{k-1}, z\right\} \backslash\left\{v_{i}\right\}$. This is again a contradiction.
From Claim 3 we see that $G$ consists of a complete set on $k$ vertices together with $n-k>0$ isolated vertices. This is a contradiction as $\delta(G) \geqslant 1$.
Remark. We do not know if the result is best possible or whether it can be improved to show $\delta(G) \geqslant 2022$.
## GEOMETRY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nC6.",
"solution_match": "\nSolution"
}
|
44991854-8bef-5e74-b29d-1a4aef278b49
| 606,193
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
1. Since the triangles $B A D, K A D$ and $K D E$ are isosceles, then $\angle B A D=\angle B D A$ and $\angle K A D=\angle K D A$ and $\angle K D E=\angle K E D$. Therefore,
$$
\angle B A K=\angle B A D-\angle K A D=\angle B D A-\angle K D A=\angle K D E=\angle K E D=180^{\circ}-\angle B E K .
$$
So the points $B, E, K, A$ are concyclic. Similarly the points $C, D, K, A$ are also concyclic.
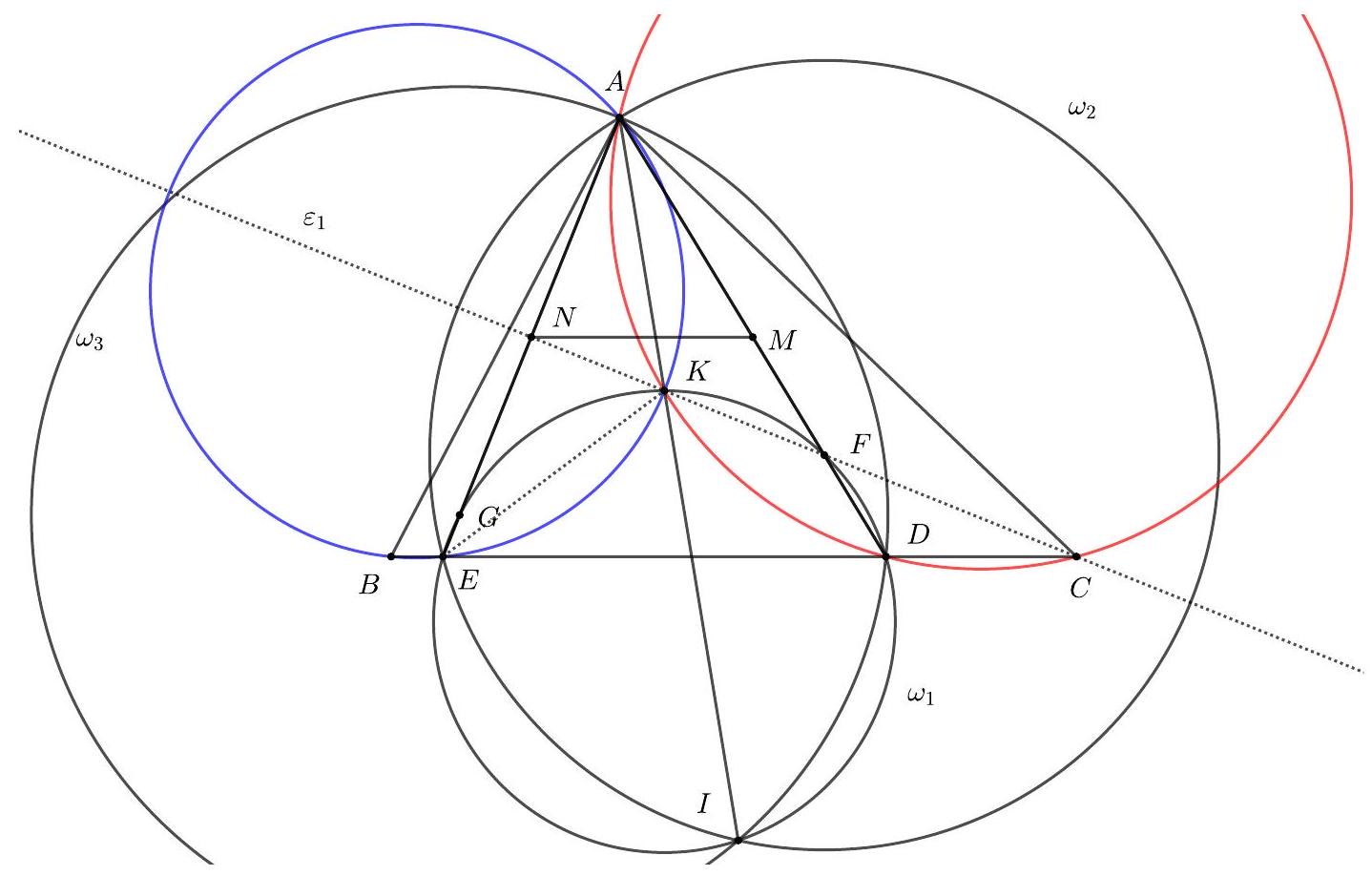
Let $M, N$ be the midpoints of $A D$ and $A E$ respectively. Since the triangle $A C E$ is isosceles, the perpendicular bisector of $A E$, say $\varepsilon_{1}$, passes through the points $C, K$ and $N$. Similarly, the perpendicular bisector of $A D$, say $\varepsilon_{2}$, passes through the points $B, K$ and $M$. Therefore the points $F, G$ lie on $\varepsilon_{1}$ and $\varepsilon_{2}$ respectively. Thus, using also the fact that $A K D C$ is a cyclic quadrilteral we get that
$$
\angle F D C=\angle A D C=\angle A K C=\angle E K C=\angle E K F .
$$
So the point $F$ lies on the circle $\omega_{1}$. Similarly $G$ also lies on $\omega_{1}$.
Let $I$ be the point of intersection of the line $A K$ with $\omega_{1}$. The triangles $A K F$ and $E K F$ are equal, so $\angle K A F=\angle K E F$. Since also $K, E, F, I$ all belong on $\omega_{1}$ then
$$
\angle K A F=\angle K E F=\angle F I K .
$$
It follows that $F I=F A=F E$. Therefore $I$ lies on $\omega_{2}$ as well. Similarly it also lies on $\omega_{3}$. So the circles $\omega_{1}, \omega_{2}, \omega_{3}$ all pass through $I$ which lies on line $A K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
1. Since the triangles $B A D, K A D$ and $K D E$ are isosceles, then $\angle B A D=\angle B D A$ and $\angle K A D=\angle K D A$ and $\angle K D E=\angle K E D$. Therefore,
$$
\angle B A K=\angle B A D-\angle K A D=\angle B D A-\angle K D A=\angle K D E=\angle K E D=180^{\circ}-\angle B E K .
$$
So the points $B, E, K, A$ are concyclic. Similarly the points $C, D, K, A$ are also concyclic.

Let $M, N$ be the midpoints of $A D$ and $A E$ respectively. Since the triangle $A C E$ is isosceles, the perpendicular bisector of $A E$, say $\varepsilon_{1}$, passes through the points $C, K$ and $N$. Similarly, the perpendicular bisector of $A D$, say $\varepsilon_{2}$, passes through the points $B, K$ and $M$. Therefore the points $F, G$ lie on $\varepsilon_{1}$ and $\varepsilon_{2}$ respectively. Thus, using also the fact that $A K D C$ is a cyclic quadrilteral we get that
$$
\angle F D C=\angle A D C=\angle A K C=\angle E K C=\angle E K F .
$$
So the point $F$ lies on the circle $\omega_{1}$. Similarly $G$ also lies on $\omega_{1}$.
Let $I$ be the point of intersection of the line $A K$ with $\omega_{1}$. The triangles $A K F$ and $E K F$ are equal, so $\angle K A F=\angle K E F$. Since also $K, E, F, I$ all belong on $\omega_{1}$ then
$$
\angle K A F=\angle K E F=\angle F I K .
$$
It follows that $F I=F A=F E$. Therefore $I$ lies on $\omega_{2}$ as well. Similarly it also lies on $\omega_{3}$. So the circles $\omega_{1}, \omega_{2}, \omega_{3}$ all pass through $I$ which lies on line $A K$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution"
}
|
54abb5db-fb59-538f-a6d5-28a0c7379e6d
| 606,206
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
2. Let $M$ the midpoint of $A D$. Then $B M$ is the perpendicular bisector of $A D$, because the triangle $A B D$ is isosceles. $K M$ is also the perpendicular bisector of $A D$, because the point $K$ is the circumcenter of the triangle $A E D$. So points $B, G, K, M$ are collinear and $G M$ is also the perpendicular bisector of $A D$. Therefore $G D=G A$ and so $A$ belongs on $\omega_{3}$. Similarly $A$ belongs on $\omega_{2}$.
Since $A D G$ is isosceles with $G A=G D$, it follows that $\angle E G D=2 \angle G A D=2 \angle E A D$. Since $A F E$ is isosceles with $F A=F E$, it follows that $\angle E F D=2 \angle F A E=2 \angle E A D$. We also have $E K D=2 \angle E A D$ as $K$ is the circumcenter of the triangle $E A D$. From the last three equalities it follows that $F, G$ belong on $\omega_{1}$.
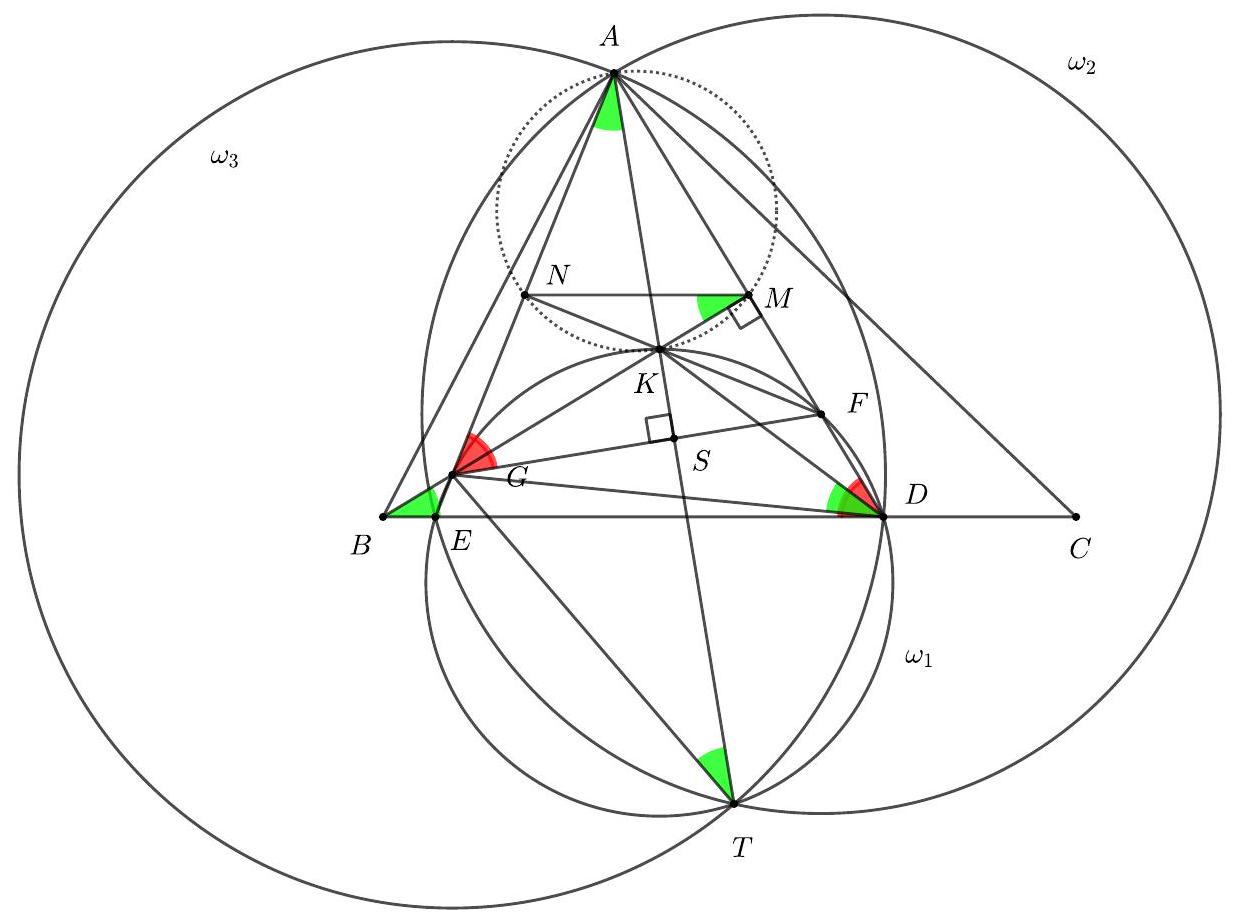
Let $T \neq A$ be the second point of intersection of the circles $\omega_{2}, \omega_{3}$ and let $S=A T \cap F G$. Let $N$ be the midpoint of $A E$. Since $\angle A M K=\angle A N K=90^{\circ}$, then the points $A, M, K, N$ are concyclic and therefore $\angle N A K=\angle N M K$. Since $N M$ is parallel to $E D(M, N$ midpoints of $A D, A E)$ then $\angle N M K=\angle D B M=90^{\circ}-\angle M D B$. Since also $D, E, G, F$ are concyclic, then $\angle M D B=\angle F G N=90^{\circ}-\angle G A S$. From the above, it follows that $\angle N A K=\angle G A S$ and so $A, K, S$ are collinear. By definition of $S$, we get that $T$ also belongs on the same line.
Since $G F$ is the perpendicular bisector of $A T$ then $\angle G A K=\angle G A S=\angle G T S=\angle G T K$. But since $G K$ is the perpendiuclar bisector of $A D$ we also have $\angle G A K=\angle G D K$. Thus $\angle G T K=\angle G D K$ showing that $T$ belongs to $\omega_{1}$ as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C<B C$. On the side $B C$ we consider points $D$ and $E$ such that $B A=B D$ and $C E=C A$. Let $K$ be the circumcenter of triangle $A D E$ and let $F, G$ be the points of intersection of the lines $A D, K C$ and $A E, K B$ respectively. Let $\omega_{1}$ be the circumcircle of triangle $K D E, \omega_{2}$ the circle with center $F$ and radius $F E$, and $c_{3}$ the circle with center $G$ and radius $G D$.
Prove that $\omega_{1}, \omega_{2}$ and $\omega_{3}$ pass through the same point and that this point of intersection lies on the line $A K$.
Proposed by Greece
|
2. Let $M$ the midpoint of $A D$. Then $B M$ is the perpendicular bisector of $A D$, because the triangle $A B D$ is isosceles. $K M$ is also the perpendicular bisector of $A D$, because the point $K$ is the circumcenter of the triangle $A E D$. So points $B, G, K, M$ are collinear and $G M$ is also the perpendicular bisector of $A D$. Therefore $G D=G A$ and so $A$ belongs on $\omega_{3}$. Similarly $A$ belongs on $\omega_{2}$.
Since $A D G$ is isosceles with $G A=G D$, it follows that $\angle E G D=2 \angle G A D=2 \angle E A D$. Since $A F E$ is isosceles with $F A=F E$, it follows that $\angle E F D=2 \angle F A E=2 \angle E A D$. We also have $E K D=2 \angle E A D$ as $K$ is the circumcenter of the triangle $E A D$. From the last three equalities it follows that $F, G$ belong on $\omega_{1}$.

Let $T \neq A$ be the second point of intersection of the circles $\omega_{2}, \omega_{3}$ and let $S=A T \cap F G$. Let $N$ be the midpoint of $A E$. Since $\angle A M K=\angle A N K=90^{\circ}$, then the points $A, M, K, N$ are concyclic and therefore $\angle N A K=\angle N M K$. Since $N M$ is parallel to $E D(M, N$ midpoints of $A D, A E)$ then $\angle N M K=\angle D B M=90^{\circ}-\angle M D B$. Since also $D, E, G, F$ are concyclic, then $\angle M D B=\angle F G N=90^{\circ}-\angle G A S$. From the above, it follows that $\angle N A K=\angle G A S$ and so $A, K, S$ are collinear. By definition of $S$, we get that $T$ also belongs on the same line.
Since $G F$ is the perpendicular bisector of $A T$ then $\angle G A K=\angle G A S=\angle G T S=\angle G T K$. But since $G K$ is the perpendiuclar bisector of $A D$ we also have $\angle G A K=\angle G D K$. Thus $\angle G T K=\angle G D K$ showing that $T$ belongs to $\omega_{1}$ as well.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG1.",
"solution_match": "\nSolution"
}
|
54abb5db-fb59-538f-a6d5-28a0c7379e6d
| 606,206
|
Let $I$ and $O$ be the incenter and the circumcenter of a triangle $A B C$, respectively, and let $s_{a}$ be the exterior bisector of angle $\angle B A C$. The line through $I$ perpendicular to $I O$ meets the lines $B C$ and $s_{a}$ at points $P$ and $Q$, respectively. Prove that $I Q=2 I P$.
## Proposed by Serbia
|
Denote by $I_{b}$ and $I_{c}$ the respective excenters opposite to $B$ and $C$. Also denote the midpoint of side $B C$ by $D$, the midpoint of the arc $B A C$ by $M$, and the midpoint of segment $A M$ by $N$. Recall that $M$ is on the perpendicular bisector of $B C$, i.e. on line $O D$. Points $I, O, D, P$ lie on the circle with diameter $O P$, whereas points $I, O, Q, N$ lie on the circle with diameter $O Q$. Thus $\angle I O P=\angle I D P$ and $\angle I O Q=180^{\circ}-\angle I N Q=\angle I N A$. So the triangles $I A N$ and $Q I O$ are similar.
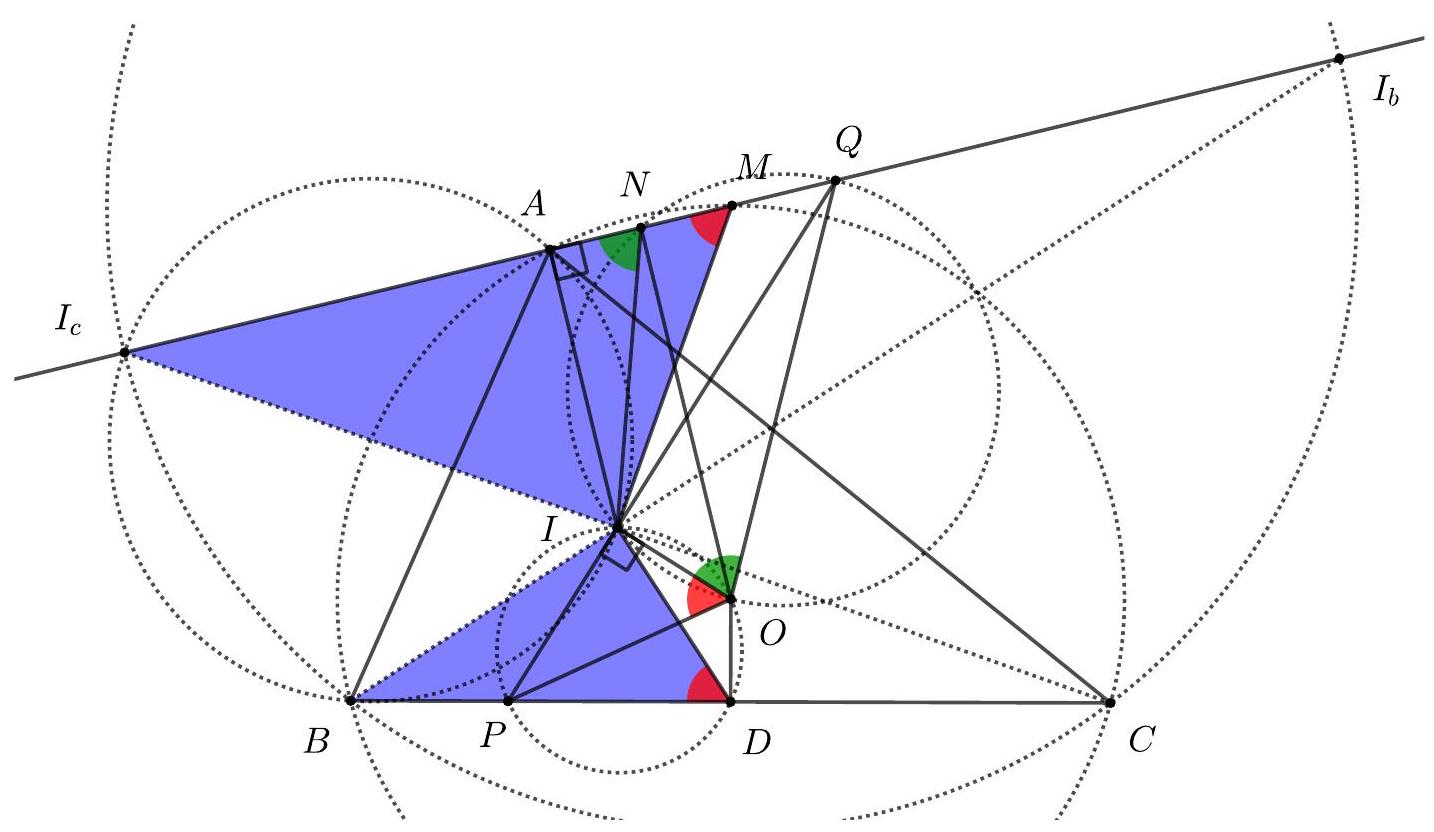
On the other hand, points $B, C, I_{b}, I_{c}$ are on the circle with diameter $I_{b} I_{c}$, so the triangles $I B C$ and $I I_{c} I_{b}$ are similar. We have $\angle I I_{c} A=\angle C I_{c} I_{b}=\angle C B I_{b}=\frac{1}{2} \beta$. Since also $\angle I B A=$ $\frac{1}{2} \beta=\angle I I_{c} A$ then we deduce (the known fact) that $I_{c}, A, I, B$ are concyclic. Thus $\angle B I_{c} A=$ $180^{\circ}-A I B=\frac{1}{2}(\alpha+\beta)$. Since also $I_{c} M B=A M B=A C B=\gamma$, then we also have that $\angle I_{c} B M=\angle B I_{c} A=\frac{1}{2}(\alpha+\beta)$. We deduce that $I_{c} M=M B=M C=I_{b} M$, i.e. $M$ is the midpoint of $I_{b} I_{c}$.
It follows that the triangles $I B D$ and $I I_{c} M$ are similar, so $\angle I O P=\angle I D P=\angle I M A$. Thus the triangles $O I P$ and $M A I$ are similar. Therefore
$$
\frac{I Q}{I O}=\frac{I A}{A N}=\frac{2 I A}{A M}=\frac{2 I P}{I O} .
$$
Thus $I Q=2 I P$.
|
I Q=2 I P
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ and $O$ be the incenter and the circumcenter of a triangle $A B C$, respectively, and let $s_{a}$ be the exterior bisector of angle $\angle B A C$. The line through $I$ perpendicular to $I O$ meets the lines $B C$ and $s_{a}$ at points $P$ and $Q$, respectively. Prove that $I Q=2 I P$.
## Proposed by Serbia
|
Denote by $I_{b}$ and $I_{c}$ the respective excenters opposite to $B$ and $C$. Also denote the midpoint of side $B C$ by $D$, the midpoint of the arc $B A C$ by $M$, and the midpoint of segment $A M$ by $N$. Recall that $M$ is on the perpendicular bisector of $B C$, i.e. on line $O D$. Points $I, O, D, P$ lie on the circle with diameter $O P$, whereas points $I, O, Q, N$ lie on the circle with diameter $O Q$. Thus $\angle I O P=\angle I D P$ and $\angle I O Q=180^{\circ}-\angle I N Q=\angle I N A$. So the triangles $I A N$ and $Q I O$ are similar.

On the other hand, points $B, C, I_{b}, I_{c}$ are on the circle with diameter $I_{b} I_{c}$, so the triangles $I B C$ and $I I_{c} I_{b}$ are similar. We have $\angle I I_{c} A=\angle C I_{c} I_{b}=\angle C B I_{b}=\frac{1}{2} \beta$. Since also $\angle I B A=$ $\frac{1}{2} \beta=\angle I I_{c} A$ then we deduce (the known fact) that $I_{c}, A, I, B$ are concyclic. Thus $\angle B I_{c} A=$ $180^{\circ}-A I B=\frac{1}{2}(\alpha+\beta)$. Since also $I_{c} M B=A M B=A C B=\gamma$, then we also have that $\angle I_{c} B M=\angle B I_{c} A=\frac{1}{2}(\alpha+\beta)$. We deduce that $I_{c} M=M B=M C=I_{b} M$, i.e. $M$ is the midpoint of $I_{b} I_{c}$.
It follows that the triangles $I B D$ and $I I_{c} M$ are similar, so $\angle I O P=\angle I D P=\angle I M A$. Thus the triangles $O I P$ and $M A I$ are similar. Therefore
$$
\frac{I Q}{I O}=\frac{I A}{A N}=\frac{2 I A}{A M}=\frac{2 I P}{I O} .
$$
Thus $I Q=2 I P$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG2.",
"solution_match": "\nSolution."
}
|
56637cce-8293-5a90-a33f-d2de5a316bf2
| 606,225
|
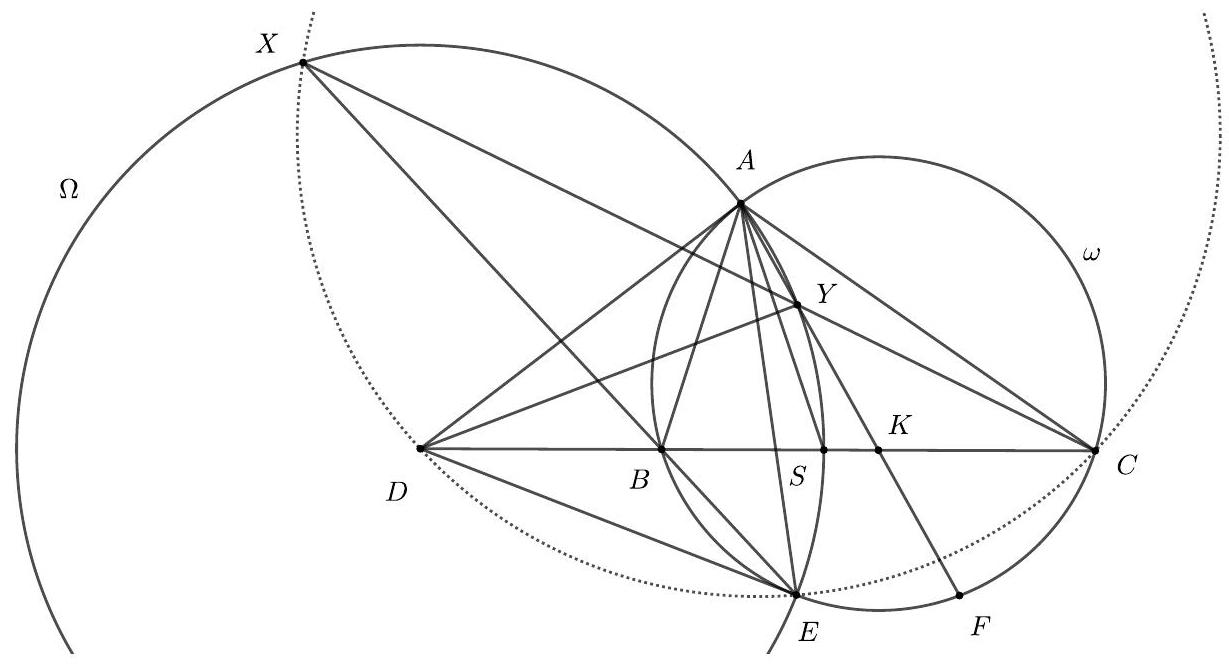
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
1. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.
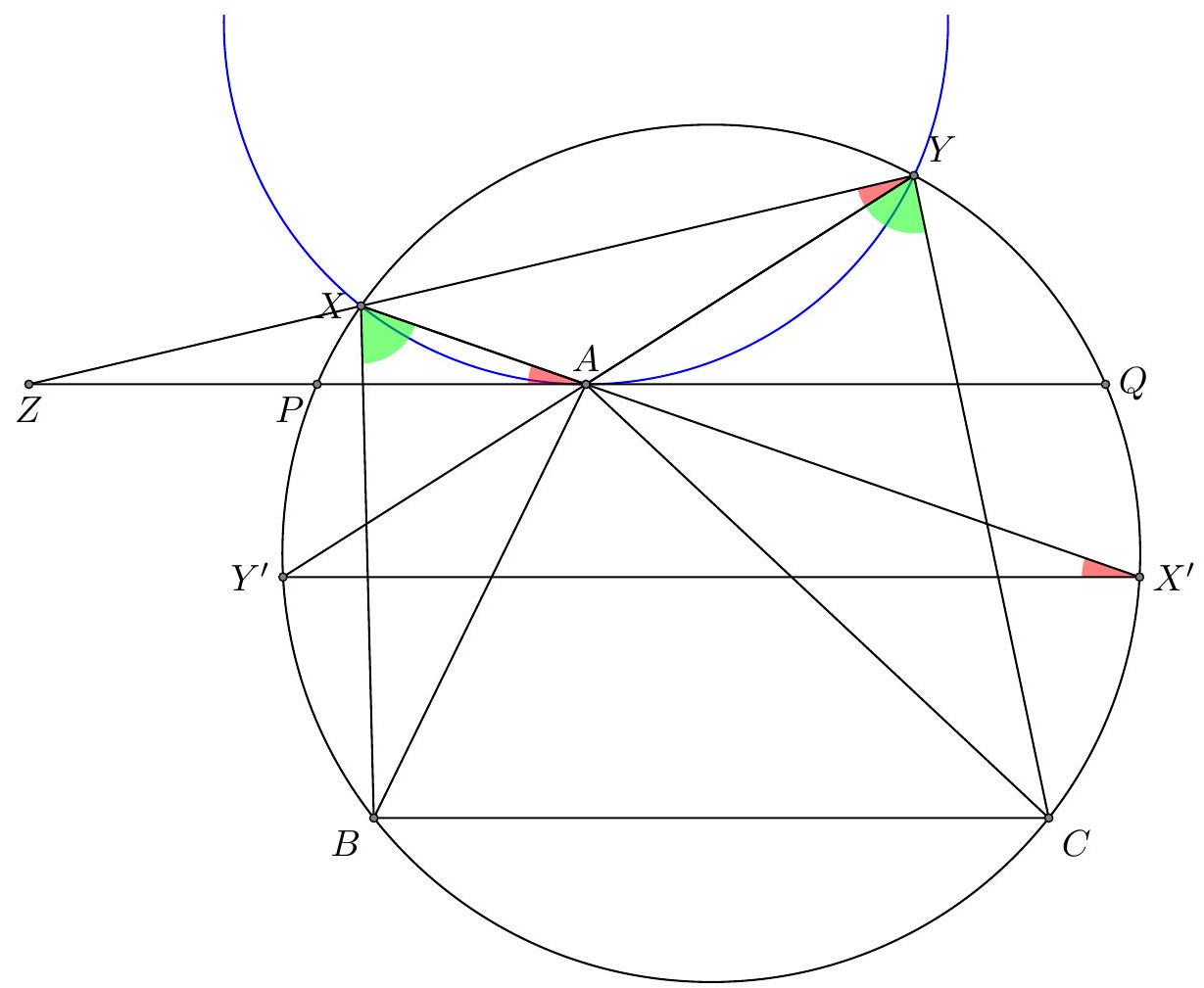
Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
1. Extend $X A$ and $Y A$ to meet $\omega$ again at $X^{\prime}$ and $Y^{\prime}$ respectively. We then have that:
$$
\angle Y^{\prime} Y C=\angle A Y C=\angle B X A=\angle B X X^{\prime} .
$$
so $B C X^{\prime} Y^{\prime}$ is an isosceles trapezium and hence $X^{\prime} Y^{\prime} \| B C$.

Let $\ell$ be the line through $A$ parallel to $B C$ and let $\ell$ intersect $\omega$ at $P, Q$ with $P$ on the opposite side of $A B$ to $C$. As $X^{\prime} Y^{\prime}\|B C\| P Q$ then
$$
\angle X A P=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A
$$
which shows that $\ell$ is tangent to the circumcircle of triangle $A X Y$. Let $X Y$ intersect $P Q$ at $Z$. By power of a point we have that
$$
Z A^{2}=Z X \cdot Z Y=Z P \cdot Z Q
$$
As $P, Q$ are independent of the positions of $X, Y$, this shows that $Z$ is fixed and hence $X Y$ passes through a fixed point.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution"
}
|
6ce0d00a-c1dc-5d8b-9862-f0d02e9db389
| 606,236
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
2. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.
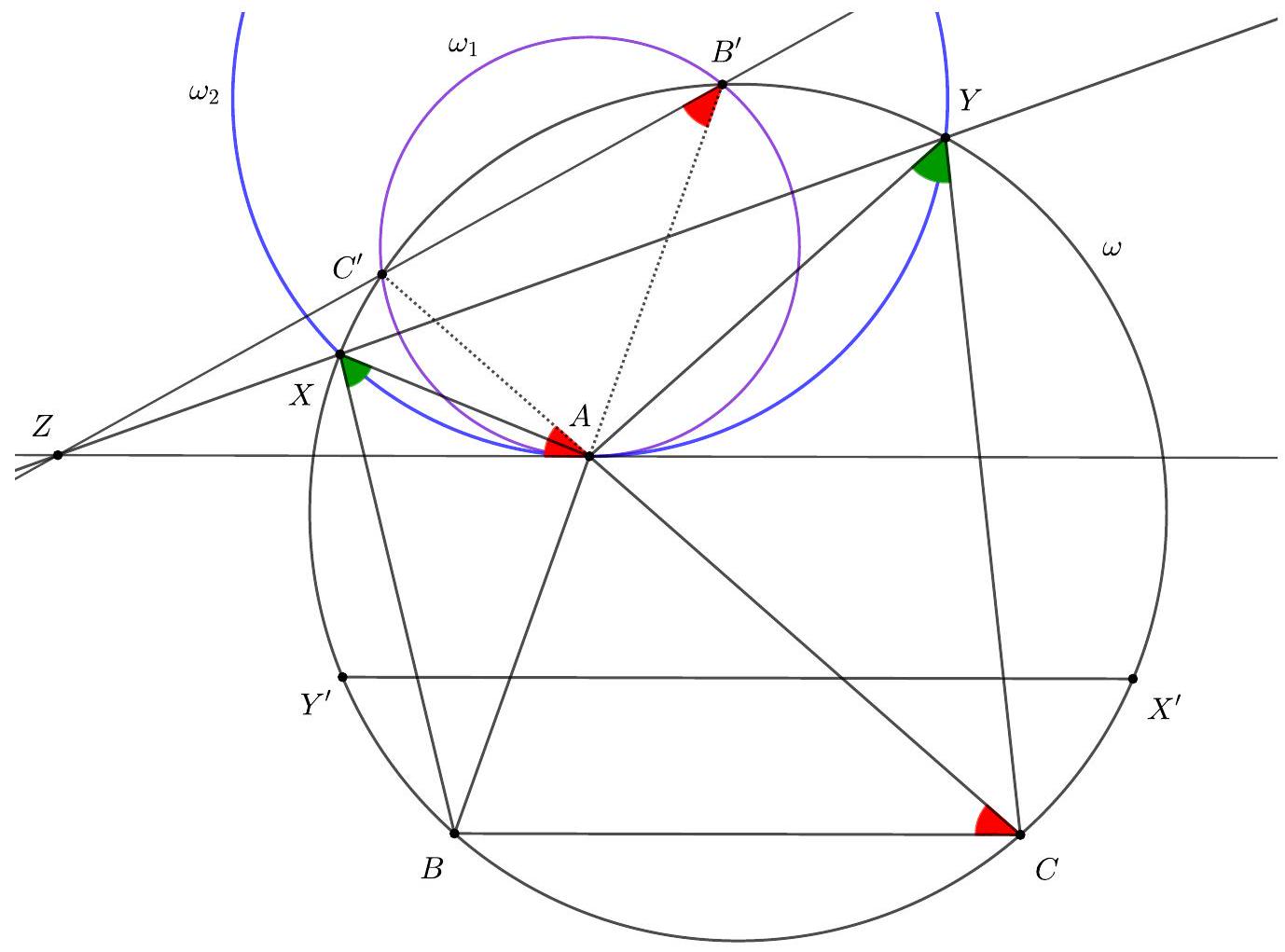
We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$. Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\omega_{2}$ ) and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
Remark: The condition that $A B<A C$ ensures that the point $Z$ exists (rather than being at infinity). If $X Y\|\ell\| B C$ then $A X=A Y$ and $X B=Y C$ so, as $\angle B X A=\angle A Y C$, we would have $\triangle A X B \cong \triangle A Y C$ and hence $A B=A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B<A C$. Let $\omega$ be a circle passing through $B, C$ and assume that $A$ is inside $\omega$. Suppose $X, Y$ lie on $\omega$ such that $\angle B X A=\angle A Y C$ and $X$ lies on the opposite side of $A B$ to $C$ while $Y$ lies on the opposite side of $A C$ to $B$.
Show that, as $X, Y$ vary on $\omega$, the line $X Y$ passes through a fixed point.
## Proposed by United Kingdom
|
2. Let $B^{\prime}$ and $C^{\prime}$ be the points of intersection of the lines $A B$ and $A C$ with $\omega$ respectively and let $\omega_{1}$ be the circumcircle of the triangle $A B^{\prime} C^{\prime}$. Let $\varepsilon$ be the tangent to $\omega_{1}$ at the point $A$. Because $A B<A C$ the lines $B^{\prime} C^{\prime}$ and $\varepsilon$ intersects at a point $Z$ which is fixed and independent of $X$ and $Y$.

We have
$$
\angle Z A C^{\prime}=\angle C^{\prime} B^{\prime} A=\angle C^{\prime} B^{\prime} B=\angle C^{\prime} C B .
$$
Therefore, $\varepsilon \| B C$.
Let $X^{\prime}, Y^{\prime}$ be the points of intersection of the lines $X A, Y A$ with $\omega$ respecively. From the hypothesis we have $\angle B X X^{\prime}=\angle Y^{\prime} Y C$. Therefore
$$
\widehat{B X^{\prime}}=\widehat{Y^{\prime} C} \Longrightarrow \widehat{B C}+\widehat{C X^{\prime}}=\widehat{Y^{\prime} B}+\widehat{B C} \Longrightarrow \widehat{C X^{\prime}}=\widehat{Y^{\prime} B}
$$
and so $X^{\prime} Y^{\prime}\|B C\| \varepsilon$. Thus
$$
\angle X A Z=\angle X X^{\prime} Y^{\prime}=\angle X Y Y^{\prime}=\angle X Y A .
$$
From the last equality we have that $\varepsilon$ is also tangent to the circmucircle $\omega_{2}$ of the triangle $X A Y$. Consider now the radical centre of the circles $\omega, \omega_{1}, \omega_{2}$. This is the point of intersection of the radical axes $B^{\prime} C^{\prime}\left(\right.$ of $\omega$ and $\left.\omega_{1}\right), \varepsilon\left(\right.$ of $\omega_{1}$ and $\omega_{2}$ ) and $X Y$ (of $\omega$ and $\omega_{2}$ ).
This must be point $Z$ and therefore the variable line $X Y$ passes through the fixed point $Z$.
Remark: The condition that $A B<A C$ ensures that the point $Z$ exists (rather than being at infinity). If $X Y\|\ell\| B C$ then $A X=A Y$ and $X B=Y C$ so, as $\angle B X A=\angle A Y C$, we would have $\triangle A X B \cong \triangle A Y C$ and hence $A B=A C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG3.",
"solution_match": "\nSolution"
}
|
6ce0d00a-c1dc-5d8b-9862-f0d02e9db389
| 606,236
|
Let $A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$. Let the height from $A$ cut its side $B C$ at $D$. Let $I, I_{B}, I_{C}$ be the incenters of triangles $A B C, A B D, A C D$ respectively. Let also $E_{B}, E_{C}$ be the excenters of $A B C$ with respect to vertices $B$ and $C$ respectively. If $K$ is the point of intersection of the circumcircles of $E_{C} I B_{I}$ and $E_{B} I C_{I}$, show that $K I$ passes through the midpoint $M$ of side $B C$.
## Proposed by Greece
|
Since $\angle E_{C} B I=90^{\circ}=I C E_{B}$, we conclude that $E_{C} B C E_{B}$ is cyclic. Moreover, we have that
$$
\angle B A I_{B}=\frac{1}{2} \angle B A D=\frac{1}{2} \widehat{C},
$$
so $A I_{B} \perp C I$. Similarly $A I_{C} \perp B I$. Therefore is the orthocenter of triangle $A I_{B} I_{C}$. It follows that
$$
\angle I I_{B} I_{C}=90^{\circ}-\angle A I_{C} I_{B}=\angle I A I_{C}=45^{\circ}-\angle I_{C} A C=45^{\circ}-\frac{1}{2} \widehat{B}=\frac{1}{2} \widehat{C}
$$
Therefore $I_{B} I_{C} C B$ is cyclic. Since $A E_{B} C I$ is also cyclic (on a circle of diameter $I E_{B}$ ) then
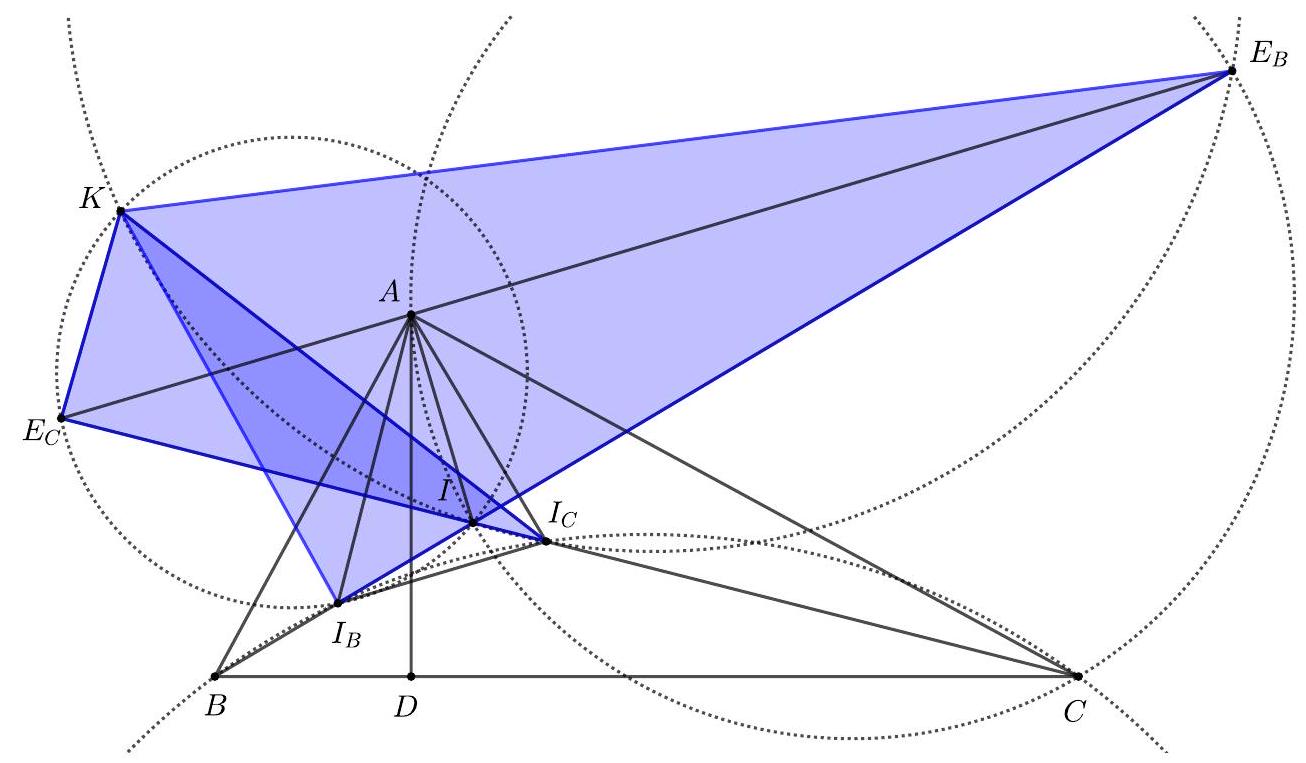
$$
\angle E_{C} E_{B} B=\angle A C I=\frac{1}{2} \widehat{C}=\angle I I_{B} I_{C},
$$
therefore $I_{B} I_{C} \| E_{B} E_{C}$.
From the inscribed quadrilaterals we get that
$$
\angle K I_{C} I=\angle K E_{B} I \quad \text { and } \quad K E_{C} I=\angle K I_{B} I,
$$
which implies that the triangles $K E_{C} I_{C}$ and $K I_{B} E_{B}$ are similar. So
$$
\frac{d\left(K, E_{C} I_{C}\right)}{d\left(K, E_{B} I_{B}\right)}=\frac{E_{C} I_{C}}{E_{B} I_{B}}
$$
But $I_{B} I_{C} \| E_{B} E_{C}$ and $I_{B} I_{C} C B$ is cyclic, therefore
$$
\frac{E_{C} I_{C}}{E_{B} I_{B}}=\frac{I I_{C}}{I I_{B}}=\frac{I B}{I C} .
$$
We deduce that
$$
\frac{d(K, I C)}{d(K, I B)}=\frac{I B}{I C},
$$
i.e. the distances of $K$ to the sides $I C$ and $I B$ are inversly analogous to the lenghts of these sides. So by a well known property of the median, $K$ lies on the median of the triangle IBC. (The last property of the median can be proved either by the law of sines, or by taking the distances of the distances of the median $M$ to the sides and prove by Thales theorem that $M, I, K$ are collinear.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\angle B A C=90^{\circ}$. Let the height from $A$ cut its side $B C$ at $D$. Let $I, I_{B}, I_{C}$ be the incenters of triangles $A B C, A B D, A C D$ respectively. Let also $E_{B}, E_{C}$ be the excenters of $A B C$ with respect to vertices $B$ and $C$ respectively. If $K$ is the point of intersection of the circumcircles of $E_{C} I B_{I}$ and $E_{B} I C_{I}$, show that $K I$ passes through the midpoint $M$ of side $B C$.
## Proposed by Greece
|
Since $\angle E_{C} B I=90^{\circ}=I C E_{B}$, we conclude that $E_{C} B C E_{B}$ is cyclic. Moreover, we have that
$$
\angle B A I_{B}=\frac{1}{2} \angle B A D=\frac{1}{2} \widehat{C},
$$
so $A I_{B} \perp C I$. Similarly $A I_{C} \perp B I$. Therefore is the orthocenter of triangle $A I_{B} I_{C}$. It follows that
$$
\angle I I_{B} I_{C}=90^{\circ}-\angle A I_{C} I_{B}=\angle I A I_{C}=45^{\circ}-\angle I_{C} A C=45^{\circ}-\frac{1}{2} \widehat{B}=\frac{1}{2} \widehat{C}
$$
Therefore $I_{B} I_{C} C B$ is cyclic. Since $A E_{B} C I$ is also cyclic (on a circle of diameter $I E_{B}$ ) then

$$
\angle E_{C} E_{B} B=\angle A C I=\frac{1}{2} \widehat{C}=\angle I I_{B} I_{C},
$$
therefore $I_{B} I_{C} \| E_{B} E_{C}$.
From the inscribed quadrilaterals we get that
$$
\angle K I_{C} I=\angle K E_{B} I \quad \text { and } \quad K E_{C} I=\angle K I_{B} I,
$$
which implies that the triangles $K E_{C} I_{C}$ and $K I_{B} E_{B}$ are similar. So
$$
\frac{d\left(K, E_{C} I_{C}\right)}{d\left(K, E_{B} I_{B}\right)}=\frac{E_{C} I_{C}}{E_{B} I_{B}}
$$
But $I_{B} I_{C} \| E_{B} E_{C}$ and $I_{B} I_{C} C B$ is cyclic, therefore
$$
\frac{E_{C} I_{C}}{E_{B} I_{B}}=\frac{I I_{C}}{I I_{B}}=\frac{I B}{I C} .
$$
We deduce that
$$
\frac{d(K, I C)}{d(K, I B)}=\frac{I B}{I C},
$$
i.e. the distances of $K$ to the sides $I C$ and $I B$ are inversly analogous to the lenghts of these sides. So by a well known property of the median, $K$ lies on the median of the triangle IBC. (The last property of the median can be proved either by the law of sines, or by taking the distances of the distances of the median $M$ to the sides and prove by Thales theorem that $M, I, K$ are collinear.)
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG4.",
"solution_match": "\nSolution."
}
|
6372dcb0-b0ae-5645-a15d-1a0d6408a8ff
| 606,252
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
1. Let $N$ be the midpoint of $B S$ which, as $S A B T$ is a parallelogram, is also the midpoint of $T A$. Using $S T\|A B\| M P$ we get:
$$
\frac{N B}{B P}=\frac{1}{2} \cdot \frac{S B}{B P}=\frac{T B}{2 \cdot B M}=\frac{T B}{B C}
$$
which shows that $T A \| C P$.
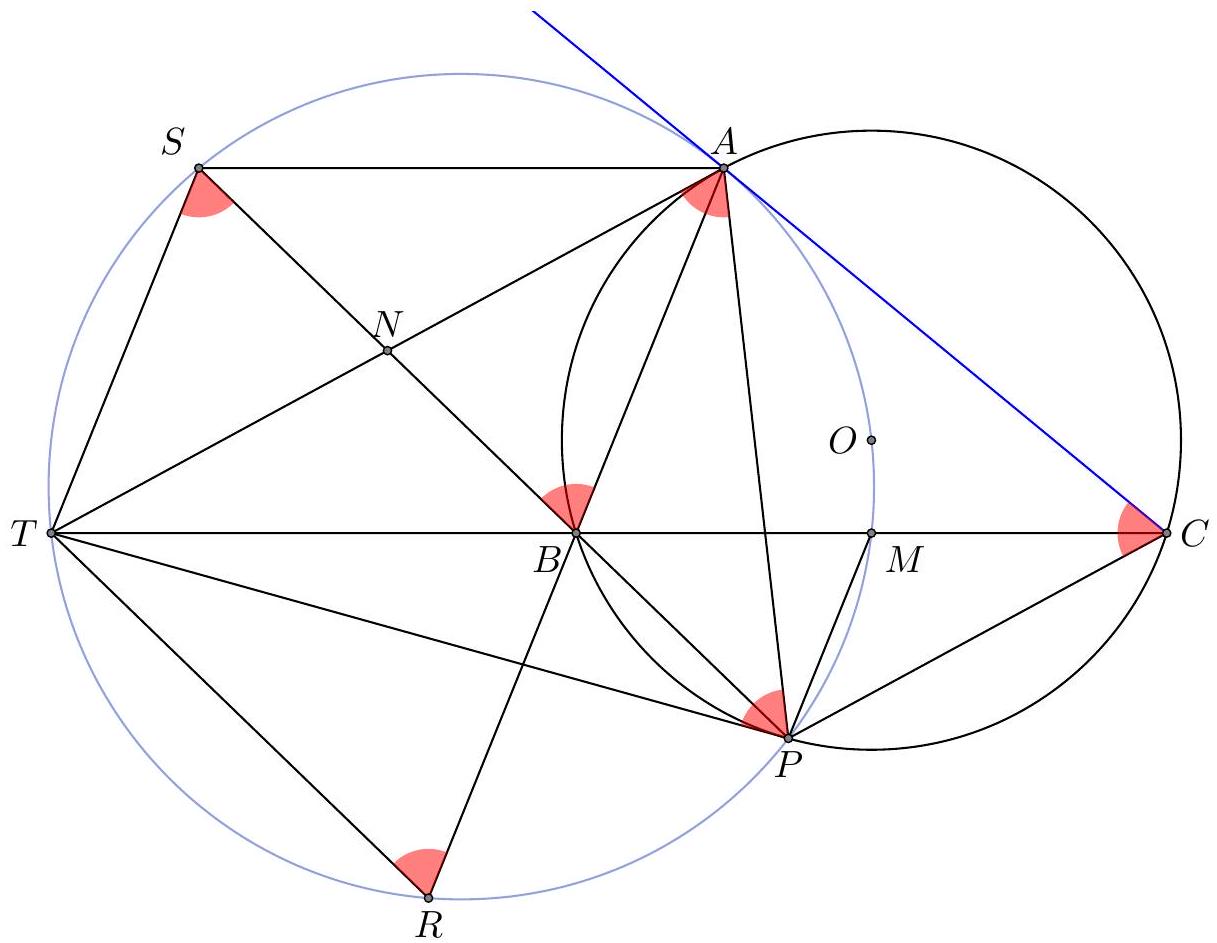
Let $\Omega$ be the circle with diameter $O T$. As $\angle O M T=90^{\circ}=\angle T A O$ we have that $A, M$ lie on $\Omega$. We now show that $P$ lies on $\Omega$. As $T A \| C P$ and $T A$ is tangent to $\Gamma$ we have that $A P=A C$, so
$$
\angle T A P=\angle A C P=\angle C P A=\angle C B A=\angle T M P
$$
where in the last step we used the fact that $M P \| A B$. This shows that $P$ lies on $\Omega$. Furthermore, this shows that $\angle O P T=90^{\circ}$ and so $T P$ is also tangent to $\Gamma$.
Now we show that $R, S$ lie on $\Omega$ which would show that $\Omega$ is the circumcircle of triangle $S T R$. For $S$, using $S T \| A B$ and that $T A$ tangent to $\Gamma$ we have
$$
\angle T S P=\angle A B S=\angle A C P=\angle T A P .
$$
For $R$, the homothety with factor 2 centred at $A$ takes $B N$ to $R T$. So $B N \| R T$ and hence
$$
\angle A R T=\angle A B S=\angle T A P=\angle A P T,
$$
where the last step follows from $T A=T P$ as they are both tangents to $\Gamma$.
Finally, we observe that as $T A$ tangent to $\Gamma$ then
$$
\angle T A C=180^{\circ}-\angle C B A=\angle A B T=\angle T S A
$$
which, by the alternate segment theorem, means that line $A C$ is tangent to $\Omega$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
1. Let $N$ be the midpoint of $B S$ which, as $S A B T$ is a parallelogram, is also the midpoint of $T A$. Using $S T\|A B\| M P$ we get:
$$
\frac{N B}{B P}=\frac{1}{2} \cdot \frac{S B}{B P}=\frac{T B}{2 \cdot B M}=\frac{T B}{B C}
$$
which shows that $T A \| C P$.

Let $\Omega$ be the circle with diameter $O T$. As $\angle O M T=90^{\circ}=\angle T A O$ we have that $A, M$ lie on $\Omega$. We now show that $P$ lies on $\Omega$. As $T A \| C P$ and $T A$ is tangent to $\Gamma$ we have that $A P=A C$, so
$$
\angle T A P=\angle A C P=\angle C P A=\angle C B A=\angle T M P
$$
where in the last step we used the fact that $M P \| A B$. This shows that $P$ lies on $\Omega$. Furthermore, this shows that $\angle O P T=90^{\circ}$ and so $T P$ is also tangent to $\Gamma$.
Now we show that $R, S$ lie on $\Omega$ which would show that $\Omega$ is the circumcircle of triangle $S T R$. For $S$, using $S T \| A B$ and that $T A$ tangent to $\Gamma$ we have
$$
\angle T S P=\angle A B S=\angle A C P=\angle T A P .
$$
For $R$, the homothety with factor 2 centred at $A$ takes $B N$ to $R T$. So $B N \| R T$ and hence
$$
\angle A R T=\angle A B S=\angle T A P=\angle A P T,
$$
where the last step follows from $T A=T P$ as they are both tangents to $\Gamma$.
Finally, we observe that as $T A$ tangent to $\Gamma$ then
$$
\angle T A C=180^{\circ}-\angle C B A=\angle A B T=\angle T S A
$$
which, by the alternate segment theorem, means that line $A C$ is tangent to $\Omega$ as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution"
}
|
05dd8176-310b-5930-85db-da7b02287d20
| 604,158
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
2. We have
$$
\angle A P S=\angle A C B=\angle T A B=\angle A T S,
$$
so $S, A, P, T$ are concyclic on a circle $\Omega$. We also have
$$
\angle P A C=\angle P B C=\angle S B T=\angle P S A
$$
so $A C$ is tangent to $\Omega$. It remains to prove that $R$ belongs on $\Omega$.
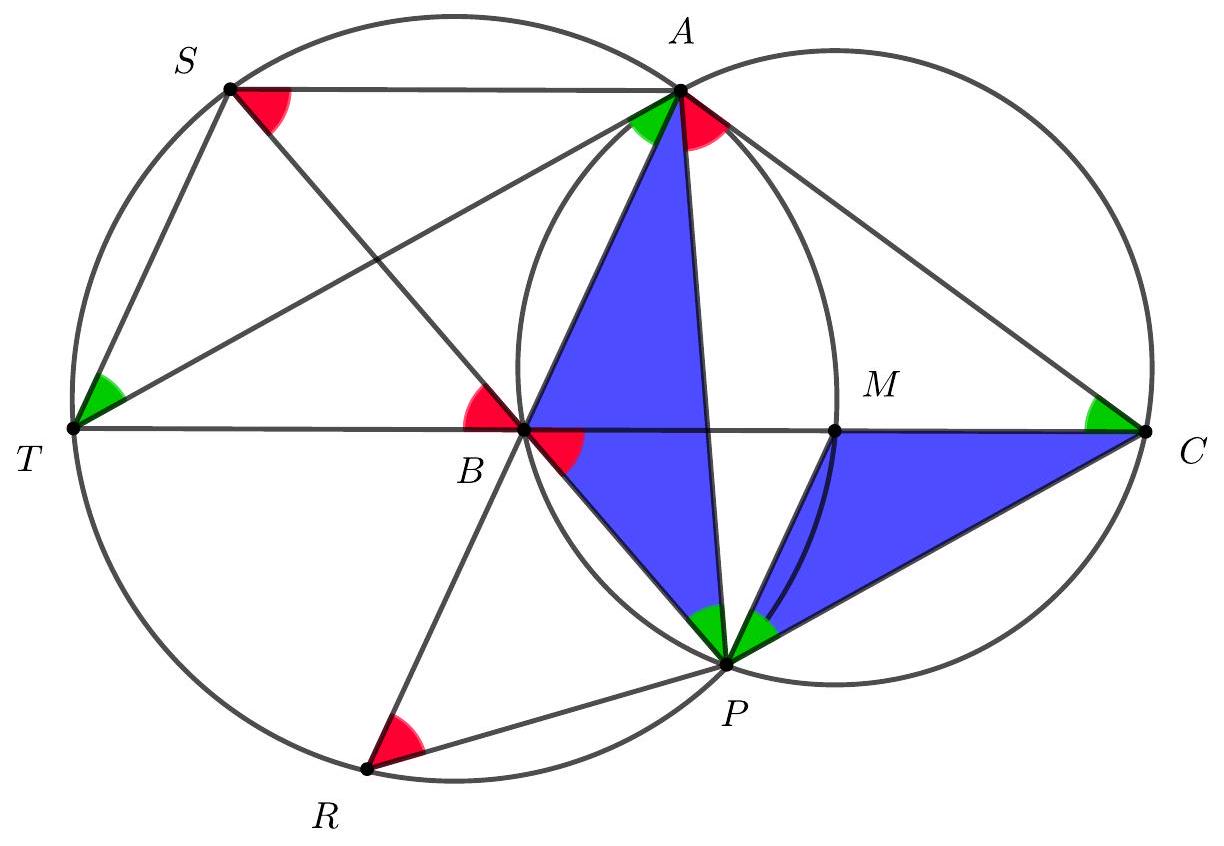
As in Solution 1 we have that $T A \| C P$. Then
$$
\angle C P M=\angle A T S=\angle A P S .
$$
Since also $\angle B A P=\angle B C P$, then the triangles $A P B$ and $C P M$ are similar. But then the triangles $B P C$ and $R A P$ are also similar as $\angle R A P=\angle B C P$ and
$$
\frac{R A}{A P}=\frac{2 B A}{A P}=\frac{2 M C}{C P}=\frac{B C}{C P} .
$$
It now follows that
$$
\angle A R P=\angle P B C=\angle A S P
$$
and therefore $R$ belongs to $\Omega$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A C>A B$ and circumcircle $\Gamma$. The tangent from $A$ to $\Gamma$ intersects $B C$ at $T$. Let $M$ be the midpoint of $B C$ and let $R$ be the reflection of $A$ in $B$. Let $S$ be a point so that $S A B T$ is a parallelogram and finally let $P$ be a point on line $S B$ such that $M P$ is parallel to $A B$.
Given that $P$ lies on $\Gamma$, prove that the circumcircle of $\triangle S T R$ is tangent to line $A C$.
## Proposed by United Kingdom
|
2. We have
$$
\angle A P S=\angle A C B=\angle T A B=\angle A T S,
$$
so $S, A, P, T$ are concyclic on a circle $\Omega$. We also have
$$
\angle P A C=\angle P B C=\angle S B T=\angle P S A
$$
so $A C$ is tangent to $\Omega$. It remains to prove that $R$ belongs on $\Omega$.

As in Solution 1 we have that $T A \| C P$. Then
$$
\angle C P M=\angle A T S=\angle A P S .
$$
Since also $\angle B A P=\angle B C P$, then the triangles $A P B$ and $C P M$ are similar. But then the triangles $B P C$ and $R A P$ are also similar as $\angle R A P=\angle B C P$ and
$$
\frac{R A}{A P}=\frac{2 B A}{A P}=\frac{2 M C}{C P}=\frac{B C}{C P} .
$$
It now follows that
$$
\angle A R P=\angle P B C=\angle A S P
$$
and therefore $R$ belongs to $\Omega$ as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG5.",
"solution_match": "\nSolution"
}
|
05dd8176-310b-5930-85db-da7b02287d20
| 604,158
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
1. Denote by $S$ the intersection point of $\Omega$ and the segment $B C$. Because $D A=D S$, we have $\angle D S A=\angle D A S$. Now using that $D A$ is tangent to $\omega$ we obtain:
$$
\angle B A S=\angle D A S-\angle D A B=\angle D S A-\angle D C A=\angle C A S .
$$
This means that the line $A S$ is the angle bisector of $\angle B A C$.
Notice that $D E$ is also tangent to $\omega$, because it is the second intersection point of $\omega$ and $\Omega$. From here, and from $D E=D X$, we see that
$$
\angle D C E=\angle B C E=\angle B E D=\angle D X E .
$$
It follows that $C E D X$ is a cyclic quadrilateral.
Since $D$ is the center of $\Omega$, then $\angle E D Y=2 \angle E X Y$. Since $C E D X$ is cyclic, we also have
$$
\angle S D E=\angle C D E=\angle C X E=\angle E X Y .
$$
Thus
$$
2 \angle S D E=2 \angle E X Y=\angle E D Y=\angle S D E+\angle S D Y
$$
and so $\angle S D E=\angle S D Y$. So we obtain
$$
\angle S A E=\frac{1}{2} \angle S D E=\frac{1}{2} \angle S D Y=\angle S A Y .
$$
Combining this with the fact that $A S$ is the angle bisector of $\angle B A C$, we see that the lines $A E$ and $A Y$ are symmetric with respect to the angle bisector of $\angle B A C$.
Now let $F$ be the second intersection point of the line $A Y$ and the circumcircle $\omega$. We have shown that $\angle B A E=\angle C A F$, which means that $B E=C F$ (two chords with the same corresponding central angle are equal). We similarly get $B F=C E$.
Since $D A$ is tangent to $\omega$, then $\angle B A D=\angle D C A$. Since also $\angle A D B=\angle C D A$ then the triangles $D A B$ and $D C A$ are similar. This gives.
$$
\frac{A B}{A C}=\frac{A D}{C D} .
$$
Similarly, the triangles $D E B$ and $D C E$ are similar, giving
$$
\frac{B E}{C E}=\frac{E D}{C D} .
$$
Combining these with $B E=C F$ and $B F=C E$ which we have shown above, and using that $D A=D E$ (tangents from the same point $D$ ), we get the relation
$$
\frac{C F}{B F}=\frac{B E}{C E}=\frac{E D}{C D}=\frac{A D}{C D}=\frac{A B}{A C} .
$$
Finally, let $K$ be the intersection point of the line $A Y$ with the segment $B C$. We have
$$
\frac{B K}{C K}=\frac{B K \sin (\angle B K A)}{B K \sin (\angle C K A)}=\frac{A B \sin (\angle B A K)}{A C \sin (\angle C A K)}=\frac{C F \sin (\angle B C F)}{B F \sin (\angle C B F)}=1 .
$$
Thus $K=M$ and $A, Y, M$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
1. Denote by $S$ the intersection point of $\Omega$ and the segment $B C$. Because $D A=D S$, we have $\angle D S A=\angle D A S$. Now using that $D A$ is tangent to $\omega$ we obtain:
$$
\angle B A S=\angle D A S-\angle D A B=\angle D S A-\angle D C A=\angle C A S .
$$
This means that the line $A S$ is the angle bisector of $\angle B A C$.

Notice that $D E$ is also tangent to $\omega$, because it is the second intersection point of $\omega$ and $\Omega$. From here, and from $D E=D X$, we see that
$$
\angle D C E=\angle B C E=\angle B E D=\angle D X E .
$$
It follows that $C E D X$ is a cyclic quadrilateral.
Since $D$ is the center of $\Omega$, then $\angle E D Y=2 \angle E X Y$. Since $C E D X$ is cyclic, we also have
$$
\angle S D E=\angle C D E=\angle C X E=\angle E X Y .
$$
Thus
$$
2 \angle S D E=2 \angle E X Y=\angle E D Y=\angle S D E+\angle S D Y
$$
and so $\angle S D E=\angle S D Y$. So we obtain
$$
\angle S A E=\frac{1}{2} \angle S D E=\frac{1}{2} \angle S D Y=\angle S A Y .
$$
Combining this with the fact that $A S$ is the angle bisector of $\angle B A C$, we see that the lines $A E$ and $A Y$ are symmetric with respect to the angle bisector of $\angle B A C$.
Now let $F$ be the second intersection point of the line $A Y$ and the circumcircle $\omega$. We have shown that $\angle B A E=\angle C A F$, which means that $B E=C F$ (two chords with the same corresponding central angle are equal). We similarly get $B F=C E$.
Since $D A$ is tangent to $\omega$, then $\angle B A D=\angle D C A$. Since also $\angle A D B=\angle C D A$ then the triangles $D A B$ and $D C A$ are similar. This gives.
$$
\frac{A B}{A C}=\frac{A D}{C D} .
$$
Similarly, the triangles $D E B$ and $D C E$ are similar, giving
$$
\frac{B E}{C E}=\frac{E D}{C D} .
$$
Combining these with $B E=C F$ and $B F=C E$ which we have shown above, and using that $D A=D E$ (tangents from the same point $D$ ), we get the relation
$$
\frac{C F}{B F}=\frac{B E}{C E}=\frac{E D}{C D}=\frac{A D}{C D}=\frac{A B}{A C} .
$$
Finally, let $K$ be the intersection point of the line $A Y$ with the segment $B C$. We have
$$
\frac{B K}{C K}=\frac{B K \sin (\angle B K A)}{B K \sin (\angle C K A)}=\frac{A B \sin (\angle B A K)}{A C \sin (\angle C A K)}=\frac{C F \sin (\angle B C F)}{B F \sin (\angle C B F)}=1 .
$$
Thus $K=M$ and $A, Y, M$ are collinear as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution"
}
|
7c76775d-c6fa-5405-b80d-9f53598d934d
| 604,185
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
2. As in Solution 1, we let $S$ be the intersection of $\Omega$ with $B S$ and obtain that $A S$ is the angle bisector of $\angle B A C$ and that $A E$ and $A Y$ are symmetric with respect to $A S$.
Let $R=\sqrt{(A B)(A C)}$ and let $\Psi$ be the map obtained by first inverting on the circle centered at $A$ of radius $R$ and the reflecting on $A S$.
By construction of $\Psi$ we have $\Psi(B)=C$ and $\Psi(C)=B$. (After the inversion $B$ maps to a point $B^{\prime}$ on $A B$ such that $(A B)\left(A B^{\prime}\right)=R^{2}=(A B)(A C)$. So after the reflection $B^{\prime}$ maps to $C$.) Since the inversion of any line not passing through $A$ is a circle passing through $A$, then $\Psi(B C)$ is a circle passing through $A$. Since it also passes through $B$ and $C$ then $\Psi(B C)=\omega$.
Because $D A$ is tangent to $\omega$ at $A$, and $D$ is the center of $\Omega$, the circles $\omega$ and $\Omega$ are orthogonal. Both reflection and inversion preserve orthogonality and both are involutions. This means that $\Psi$ is an involution that preserves orthogonality. From here we conlude that the images $\Psi(\omega)=B C$ and $\Psi(\Omega)$ are orthogonal lines.
Since $\Psi(A S)=A S, \Phi(B C)=\omega$ and $S$ belongs on $B C$, then $\Psi(S)$ is the intersection of $A S$ with $\omega$. Since $A S$ is the angle bisector of triangle $A B C$, then $\Psi(S)=N$, the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$.
Since $S$ belongs on $\Omega$ and $\Psi(\Omega)$ and $\Psi(\omega)$ are orthogonal lines, then $\Psi(\Omega)$ is the line perpendicular to $B C$ at $N$. It therefore contains the midpoint $M$ of $B C$.
The intersection point $E$ of $\omega$ and $\Omega$ maps to $\Psi(E)$, which is the intersection point of $\Psi(\omega)=B C$ and $\Psi(\Omega)=M N$, which must be equal to $M$, i.e. $\Psi(E)=M$. Because of this, we see that $A E$ and $A M$ are symmetric with respect to the angle bisector $A S$. Since also $A E$ and $A Y$ are symmetric with respect to $A S$, it follows that $A, M, Y$ are collinear as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle such that $A B<A C$. Let $\omega$ be the circumcircle of $A B C$ and assume that the tangent to $\omega$ at $A$ intersects the line $B C$ at $D$. Let $\Omega$ be the circle with center $D$ and radius $A D$. Denote by $E$ the second intersection point of $\omega$ and $\Omega$. Let $M$ be the midpoint of $B C$. If the line $B E$ meets $\Omega$ again at $X$, and the line $C X$ meets $\Omega$ for the second time at $Y$, show that $A, Y$ and $M$ are collinear.
## Proposed by North Macedonia
|
2. As in Solution 1, we let $S$ be the intersection of $\Omega$ with $B S$ and obtain that $A S$ is the angle bisector of $\angle B A C$ and that $A E$ and $A Y$ are symmetric with respect to $A S$.
Let $R=\sqrt{(A B)(A C)}$ and let $\Psi$ be the map obtained by first inverting on the circle centered at $A$ of radius $R$ and the reflecting on $A S$.
By construction of $\Psi$ we have $\Psi(B)=C$ and $\Psi(C)=B$. (After the inversion $B$ maps to a point $B^{\prime}$ on $A B$ such that $(A B)\left(A B^{\prime}\right)=R^{2}=(A B)(A C)$. So after the reflection $B^{\prime}$ maps to $C$.) Since the inversion of any line not passing through $A$ is a circle passing through $A$, then $\Psi(B C)$ is a circle passing through $A$. Since it also passes through $B$ and $C$ then $\Psi(B C)=\omega$.
Because $D A$ is tangent to $\omega$ at $A$, and $D$ is the center of $\Omega$, the circles $\omega$ and $\Omega$ are orthogonal. Both reflection and inversion preserve orthogonality and both are involutions. This means that $\Psi$ is an involution that preserves orthogonality. From here we conlude that the images $\Psi(\omega)=B C$ and $\Psi(\Omega)$ are orthogonal lines.
Since $\Psi(A S)=A S, \Phi(B C)=\omega$ and $S$ belongs on $B C$, then $\Psi(S)$ is the intersection of $A S$ with $\omega$. Since $A S$ is the angle bisector of triangle $A B C$, then $\Psi(S)=N$, the midpoint of the $\operatorname{arc} B C$ of $\omega$ not containing $A$.
Since $S$ belongs on $\Omega$ and $\Psi(\Omega)$ and $\Psi(\omega)$ are orthogonal lines, then $\Psi(\Omega)$ is the line perpendicular to $B C$ at $N$. It therefore contains the midpoint $M$ of $B C$.
The intersection point $E$ of $\omega$ and $\Omega$ maps to $\Psi(E)$, which is the intersection point of $\Psi(\omega)=B C$ and $\Psi(\Omega)=M N$, which must be equal to $M$, i.e. $\Psi(E)=M$. Because of this, we see that $A E$ and $A M$ are symmetric with respect to the angle bisector $A S$. Since also $A E$ and $A Y$ are symmetric with respect to $A S$, it follows that $A, M, Y$ are collinear as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG6.",
"solution_match": "\nSolution"
}
|
7c76775d-c6fa-5405-b80d-9f53598d934d
| 604,185
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
1. We shall use the standard notations for $A B C$, i.e. $\angle A B C=\beta, B C=a$ etc. We also write $s=\frac{a+b+c}{2}$ for the semiperimeter and $r$ for the inradius.
Let $M N$ intersect the altitude $A D(D$ lies on $B C)$ at the point $L$. We have that $\angle B A D=90^{\circ}-\beta$ and $\angle A M L=\angle B M N=\frac{\beta}{2}$. (Since $B M N$ is an isosceles triangle with $\angle M B N=180^{\circ}-\beta$.) It is known that $A M=s-b$ so by the Sine Law in the triangle $A M L$ we have
$$
\frac{A M}{\sin \angle A L M}=\frac{A L}{\sin \angle A M L} \Longrightarrow \frac{s-b}{\sin \left(90^{\circ}+\frac{\beta}{2}\right)}=\frac{A L}{\sin \frac{\beta}{2}} \Longrightarrow A L=(s-b) \tan \frac{\beta}{2}=r .
$$
Analogously we see that if $P Q$ intersects $A D$ at $L^{\prime}$, then $A L^{\prime}=r$. Therefore $L$ and $L^{\prime}$ coincide and since $A_{1}=M N \cap P Q$ by definition, we conclude that $L=L^{\prime}=A_{1}$. In particular, we can now view the point $A_{2}$ as the point on the $A$-altitude such that $A A_{2}=2 r$. Analogously $B_{2}$ and $C_{2}$ lie on the $B$-altitude and $C$-altitude, respectively, and $B B_{2}=C C_{2}=2 r$.
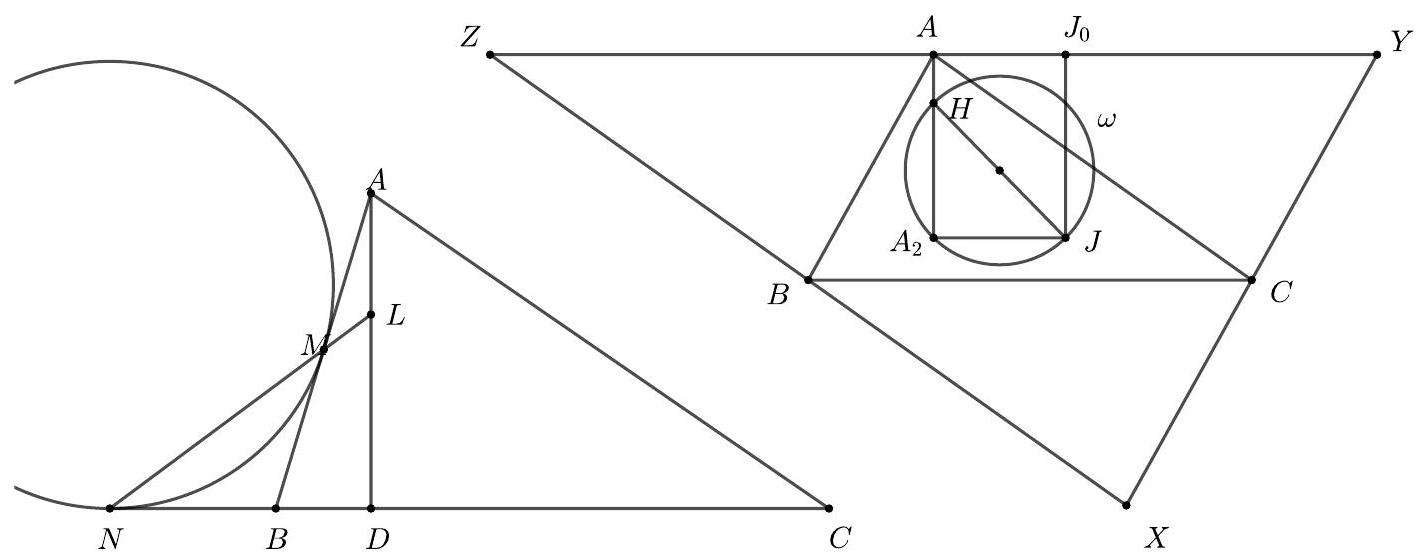
Now let $X$ be the reflection of $A$ on the midpoint of $B C$ and define $X Y Z$ analogously. So $X Y Z$ is the triangle whose midpoints of sides are $A, B$ and $C$. Let $J$ be the incenter of this triangle. As the triangles $X Y Z$ and $A B C$ are similar with ratio 2, the inradius of $X Y Z$ is equal to $2 r$. So if $J J_{0}$ is perpendicular to $Y Z$ (with $J_{0}$ on $Y Z$ ), then $A A_{2}$ and $J J_{0}$ are parallel (both perpendicular to $Y Z$ ) and equal, hence $A A_{2} J J_{0}$ is a rectangle and in particular $A_{2}$ is the foot of the perpendicular from $J$ to the $A$-altitude of $A B C$. It follows that $A_{2}, B_{2}$ and $C_{2}$ lie on the circle $\omega$ with diameter $J H$.
Now we finish with a simple angle chasing. The circle $k$ gives $\angle A_{2} B_{2} C_{2}=\angle A_{2} H C_{2}=$ $\angle 180^{\circ}-\angle A H C=\angle A B C$; similarly for the angles at $A_{2}$ and $C_{2}$. The desired similarity follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
1. We shall use the standard notations for $A B C$, i.e. $\angle A B C=\beta, B C=a$ etc. We also write $s=\frac{a+b+c}{2}$ for the semiperimeter and $r$ for the inradius.
Let $M N$ intersect the altitude $A D(D$ lies on $B C)$ at the point $L$. We have that $\angle B A D=90^{\circ}-\beta$ and $\angle A M L=\angle B M N=\frac{\beta}{2}$. (Since $B M N$ is an isosceles triangle with $\angle M B N=180^{\circ}-\beta$.) It is known that $A M=s-b$ so by the Sine Law in the triangle $A M L$ we have
$$
\frac{A M}{\sin \angle A L M}=\frac{A L}{\sin \angle A M L} \Longrightarrow \frac{s-b}{\sin \left(90^{\circ}+\frac{\beta}{2}\right)}=\frac{A L}{\sin \frac{\beta}{2}} \Longrightarrow A L=(s-b) \tan \frac{\beta}{2}=r .
$$
Analogously we see that if $P Q$ intersects $A D$ at $L^{\prime}$, then $A L^{\prime}=r$. Therefore $L$ and $L^{\prime}$ coincide and since $A_{1}=M N \cap P Q$ by definition, we conclude that $L=L^{\prime}=A_{1}$. In particular, we can now view the point $A_{2}$ as the point on the $A$-altitude such that $A A_{2}=2 r$. Analogously $B_{2}$ and $C_{2}$ lie on the $B$-altitude and $C$-altitude, respectively, and $B B_{2}=C C_{2}=2 r$.

Now let $X$ be the reflection of $A$ on the midpoint of $B C$ and define $X Y Z$ analogously. So $X Y Z$ is the triangle whose midpoints of sides are $A, B$ and $C$. Let $J$ be the incenter of this triangle. As the triangles $X Y Z$ and $A B C$ are similar with ratio 2, the inradius of $X Y Z$ is equal to $2 r$. So if $J J_{0}$ is perpendicular to $Y Z$ (with $J_{0}$ on $Y Z$ ), then $A A_{2}$ and $J J_{0}$ are parallel (both perpendicular to $Y Z$ ) and equal, hence $A A_{2} J J_{0}$ is a rectangle and in particular $A_{2}$ is the foot of the perpendicular from $J$ to the $A$-altitude of $A B C$. It follows that $A_{2}, B_{2}$ and $C_{2}$ lie on the circle $\omega$ with diameter $J H$.
Now we finish with a simple angle chasing. The circle $k$ gives $\angle A_{2} B_{2} C_{2}=\angle A_{2} H C_{2}=$ $\angle 180^{\circ}-\angle A H C=\angle A B C$; similarly for the angles at $A_{2}$ and $C_{2}$. The desired similarity follows.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution"
}
|
d91d1135-b8b9-598d-9c89-2c7e69ae59ea
| 604,216
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
2. As in Solution 1, we have that $A_{2}, B_{2}, C_{2}$ belong on the corresponding altitudes with $A A_{2}=B B_{2}=C C_{2}=2 r$. We present an approach with complex numbers (and minimal calculations) which can also complete the proof.
Set the incenter $I$ of the triangle $A B C$ to be the origin. We may assume that $r=1$. We write $a, b, c$ to denote $A^{\prime}, B^{\prime}, C^{\prime}$. Point $A$ is the intersection of the tangents to the unit circle (incircle) at $B^{\prime}$ and $C^{\prime}$ and is therefore represented by the complex number $2 b c /(b+c)$. Analogously the points $B$ and $C$ are represented by $2 a c /(a+c)$ and $2 a b /(a+b)$ respectively.
Since $A A_{2}=r=2$ and $A A_{2}$ is parallel to $I A^{\prime}$, we have that $A_{2}$ is represented by the complex number
$$
\frac{2 b c}{b+c}+2 a=\frac{2(a b+b c+c a)}{b+c}
$$
Now since $|c|=1$, then
$$
(A B)=\left|\frac{b c}{b+c}-\frac{a c}{a+c}\right|=\left|\frac{b-a}{(a+c)(b+c)}\right| .
$$
We also have
$$
\left(A_{2} B_{2}\right)=\left|\frac{2(a b+b c+c a)}{b+c}-\frac{2(a b+b c+c a)}{a+c}\right|=2|a b+b c+c a|\left(A_{2} B_{2}\right) .
$$
Analogously we get
$$
\frac{A_{2} B_{2}}{A B}=\frac{B_{2} C_{2}}{B C}=\frac{C_{2} A_{2}}{C A}=2|a b+b c+c a|
$$
So the triangle $A_{2} B_{2} C_{2}$ is similar to the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute scalene triangle. Its $C$-excircle tangent to the segment $A B$ meets $A B$ at point $M$ and the extension of $B C$ beyond $B$ at point $N$. Analogously, its $B$-excircle tangent to the segment $A C$ meets $A C$ at point $P$ and the extension of $B C$ beyond $C$ at point $Q$. Denote by $A_{1}$ the intersection point of the lines $M N$ and $P Q$, and let $A_{2}$ be defined as the point, symmetric to $A$ with respect to $A_{1}$. Define the points $B_{2}$ and $C_{2}$, analogously. Prove that $\triangle A B C$ is similar to $\triangle A_{2} B_{2} C_{2}$.
## Proposed by Bulgaria
|
2. As in Solution 1, we have that $A_{2}, B_{2}, C_{2}$ belong on the corresponding altitudes with $A A_{2}=B B_{2}=C C_{2}=2 r$. We present an approach with complex numbers (and minimal calculations) which can also complete the proof.
Set the incenter $I$ of the triangle $A B C$ to be the origin. We may assume that $r=1$. We write $a, b, c$ to denote $A^{\prime}, B^{\prime}, C^{\prime}$. Point $A$ is the intersection of the tangents to the unit circle (incircle) at $B^{\prime}$ and $C^{\prime}$ and is therefore represented by the complex number $2 b c /(b+c)$. Analogously the points $B$ and $C$ are represented by $2 a c /(a+c)$ and $2 a b /(a+b)$ respectively.
Since $A A_{2}=r=2$ and $A A_{2}$ is parallel to $I A^{\prime}$, we have that $A_{2}$ is represented by the complex number
$$
\frac{2 b c}{b+c}+2 a=\frac{2(a b+b c+c a)}{b+c}
$$
Now since $|c|=1$, then
$$
(A B)=\left|\frac{b c}{b+c}-\frac{a c}{a+c}\right|=\left|\frac{b-a}{(a+c)(b+c)}\right| .
$$
We also have
$$
\left(A_{2} B_{2}\right)=\left|\frac{2(a b+b c+c a)}{b+c}-\frac{2(a b+b c+c a)}{a+c}\right|=2|a b+b c+c a|\left(A_{2} B_{2}\right) .
$$
Analogously we get
$$
\frac{A_{2} B_{2}}{A B}=\frac{B_{2} C_{2}}{B C}=\frac{C_{2} A_{2}}{C A}=2|a b+b c+c a|
$$
So the triangle $A_{2} B_{2} C_{2}$ is similar to the triangle $A B C$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG7.",
"solution_match": "\nSolution"
}
|
d91d1135-b8b9-598d-9c89-2c7e69ae59ea
| 604,216
|
Let $A B C$ be a scalene triangle and let $I$ be its incenter. The projections of $I$ on $B C, C A$ and $A B$ are $D, E$ and $F$ respectively. Let $K$ be the reflection of $D$ over the line $A I$, and let $L$ be the second point of intersection of the circumcircles of the triangles $B F K$ and $C E K$. If $\frac{1}{3} B C=A C-A B$, prove that $D E=2 K L$.
Proposed by Romania
|
Writing $A E=A F=x, B F=B D=y$ and $C E=C D=z$, the condition $\frac{1}{3} B C=A C-A B$ translates to $y+z=3(z-y)$ giving $z=2 y$, i.e. $C D=2 B D$.
Letting $B^{\prime}$ be the reflection of $B$ on $A I$ we have that $B^{\prime}$ belongs on $A C$ with $B^{\prime} E=B F=$ $B D=\frac{1}{2} C D=\frac{1}{2} C E$ therefore $B^{\prime}$ is the midpoint of $C E$.
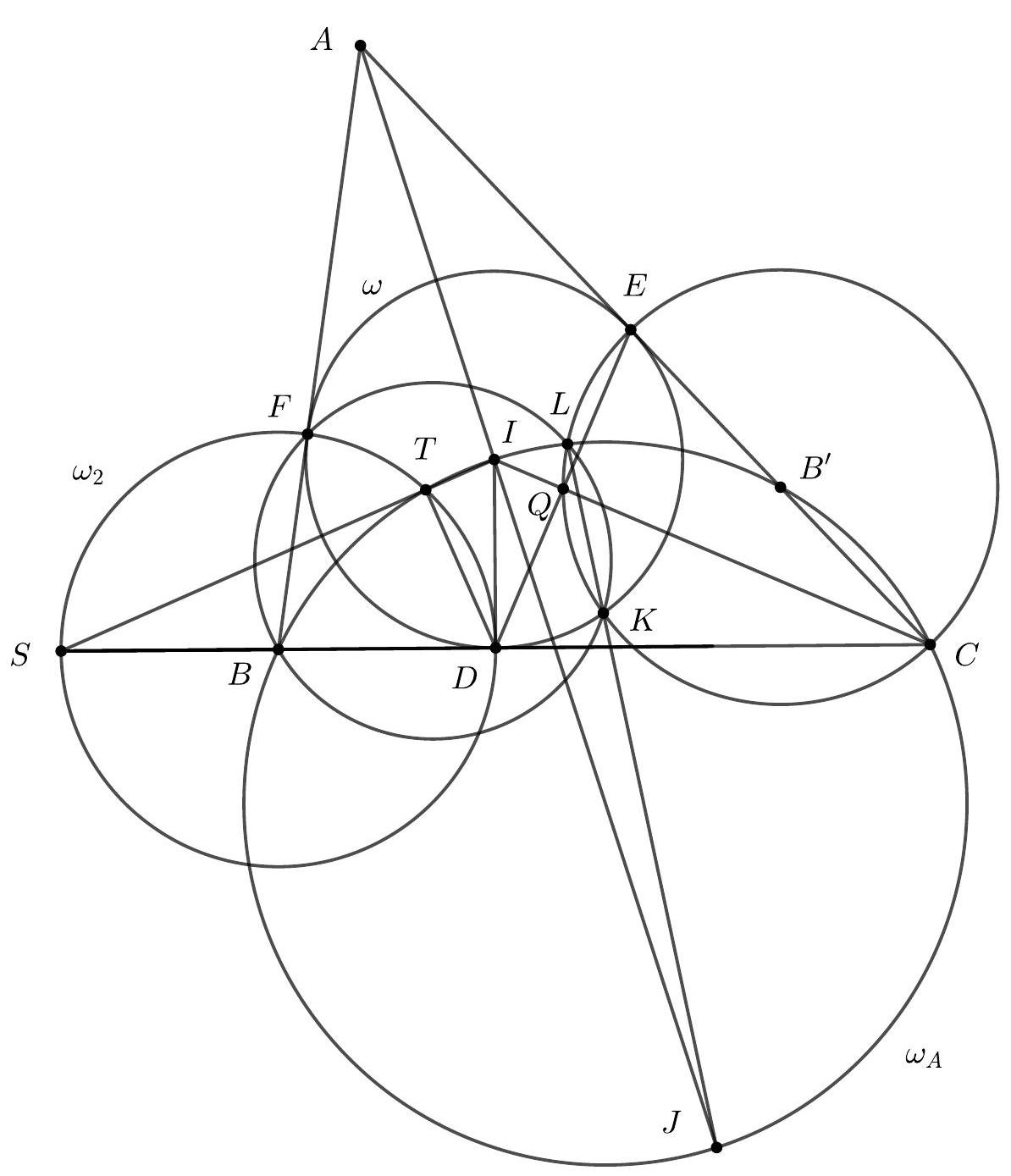
Under reflection on $A I$, the circumcircle $\omega$ of triangle $D E F$ remains fixed. Its tangent $B D$ maps to $B^{\prime} K$. So $B^{\prime} K$ is tangent to $\omega$. Since $B^{\prime} E$ is tangent to $\omega$, then $B^{\prime} E=B^{\prime} K=B^{\prime} C$. Thus $C K E$ is a right-angled triangle with diameter $C E$. If $Q$ is the midpoint of $D E$ then, since $C D=C E$, we have that $\angle C Q E=90^{\circ}$ and therefore the points $C, K, Q, L, E$ are concyclic.
Observe that
$$
\begin{aligned}
\angle B L C & =\angle B L K+\angle C L K=\angle B F K+\angle C E K=\left(180^{\circ}-\angle A F K\right)+\left(180^{\circ}-\angle A E K\right) \\
& =\angle B A C+\angle F K E=\angle B A C+\angle F D E=\angle B A C+\left(90^{\circ}-\frac{1}{2} \angle B A C\right) \\
& =90^{\circ}+\frac{1}{2} \angle B A C=\angle B I C .
\end{aligned}
$$
So $L$ belongs on the circumcircle of triangle $B I C$, i.e. on the $A$-excircle $\omega_{A}$ of triangle $A B C$.
Let $J$ be the $A$-excenter of triangle $A B C$ and recall that it is the antipodal point of $I$ on $\omega_{A}$. Then
$$
\angle C L J=\angle C B J=90^{\circ}-\frac{1}{2} \angle A B C=\angle B F D=\angle C E K=\angle C L K .
$$
So $K, L, J$ are collinear and therefore $\angle I L K=90^{\circ}$.
Let $T$ be the reflection of $L$ on $A I$. Since $L$ belongs on the circle with centre $B^{\prime}$ containing $E$ and $K$, then $L$ belongs on the circle $\omega_{2}$ with centre $B$ containing $F$ and $D$. Let $S$ be the intersection of $I T$ and $B C$. Since $K L \perp I L$, then $D T \perp I T$. It follows that $\angle I D T=90^{\circ}-\angle D I S=\angle I S D$. Since $I D$ is tangent on $\omega_{2}$, then $S$ belongs on $\omega_{2}$. Then $S D=2 B D=D C$ and so the triangles $I D C$ and $I D S$ are equal. Their height $D T$ and $D Q$ must be equal. Therefore $D E=2 D Q=2 D T=2 K L$ as required.
## NUMBER THEORY
|
D E=2 K L
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene triangle and let $I$ be its incenter. The projections of $I$ on $B C, C A$ and $A B$ are $D, E$ and $F$ respectively. Let $K$ be the reflection of $D$ over the line $A I$, and let $L$ be the second point of intersection of the circumcircles of the triangles $B F K$ and $C E K$. If $\frac{1}{3} B C=A C-A B$, prove that $D E=2 K L$.
Proposed by Romania
|
Writing $A E=A F=x, B F=B D=y$ and $C E=C D=z$, the condition $\frac{1}{3} B C=A C-A B$ translates to $y+z=3(z-y)$ giving $z=2 y$, i.e. $C D=2 B D$.
Letting $B^{\prime}$ be the reflection of $B$ on $A I$ we have that $B^{\prime}$ belongs on $A C$ with $B^{\prime} E=B F=$ $B D=\frac{1}{2} C D=\frac{1}{2} C E$ therefore $B^{\prime}$ is the midpoint of $C E$.

Under reflection on $A I$, the circumcircle $\omega$ of triangle $D E F$ remains fixed. Its tangent $B D$ maps to $B^{\prime} K$. So $B^{\prime} K$ is tangent to $\omega$. Since $B^{\prime} E$ is tangent to $\omega$, then $B^{\prime} E=B^{\prime} K=B^{\prime} C$. Thus $C K E$ is a right-angled triangle with diameter $C E$. If $Q$ is the midpoint of $D E$ then, since $C D=C E$, we have that $\angle C Q E=90^{\circ}$ and therefore the points $C, K, Q, L, E$ are concyclic.
Observe that
$$
\begin{aligned}
\angle B L C & =\angle B L K+\angle C L K=\angle B F K+\angle C E K=\left(180^{\circ}-\angle A F K\right)+\left(180^{\circ}-\angle A E K\right) \\
& =\angle B A C+\angle F K E=\angle B A C+\angle F D E=\angle B A C+\left(90^{\circ}-\frac{1}{2} \angle B A C\right) \\
& =90^{\circ}+\frac{1}{2} \angle B A C=\angle B I C .
\end{aligned}
$$
So $L$ belongs on the circumcircle of triangle $B I C$, i.e. on the $A$-excircle $\omega_{A}$ of triangle $A B C$.
Let $J$ be the $A$-excenter of triangle $A B C$ and recall that it is the antipodal point of $I$ on $\omega_{A}$. Then
$$
\angle C L J=\angle C B J=90^{\circ}-\frac{1}{2} \angle A B C=\angle B F D=\angle C E K=\angle C L K .
$$
So $K, L, J$ are collinear and therefore $\angle I L K=90^{\circ}$.
Let $T$ be the reflection of $L$ on $A I$. Since $L$ belongs on the circle with centre $B^{\prime}$ containing $E$ and $K$, then $L$ belongs on the circle $\omega_{2}$ with centre $B$ containing $F$ and $D$. Let $S$ be the intersection of $I T$ and $B C$. Since $K L \perp I L$, then $D T \perp I T$. It follows that $\angle I D T=90^{\circ}-\angle D I S=\angle I S D$. Since $I D$ is tangent on $\omega_{2}$, then $S$ belongs on $\omega_{2}$. Then $S D=2 B D=D C$ and so the triangles $I D C$ and $I D S$ are equal. Their height $D T$ and $D Q$ must be equal. Therefore $D E=2 D Q=2 D T=2 K L$ as required.
## NUMBER THEORY
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nG8.",
"solution_match": "\nSolution."
}
|
205d9864-f880-57e4-81cd-803d7ecda560
| 604,244
|
Let $n \geqslant 3$ be an integer and let
$$
M=\left\{\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}: 1 \leqslant k \leqslant n \text { and } 1 \leqslant a_{1}<\cdots<a_{k} \leqslant n\right\}
$$
be the set of the arithmetic means of the elements of all non-empty subsets of $\{1,2, \ldots, n\}$. Find $\min \{|a-b|: a, b \in M$ with $a \neq b\}$.
## Proposed by Romania
|
We observe that $M$ is composed by rational numbers of the form $a=\frac{x}{k}$, where $1 \leqslant k \leqslant n$. As the arithmetic mean of $1, \ldots, n$ is $\frac{n+1}{2}$, if we look at these rational numbers in their irreducible form, we can say that $1 \leqslant k \leqslant n-1$.
A non-zero difference $|a-b|$ with $a, b \in M$ is then of form
$$
\left|\frac{x}{k}-\frac{y}{p}\right|=\frac{\left|p_{0} x-k_{0} y\right|}{[k, p]}
$$
where $[k, p]$ is the l.c.m. of $k, p$, and $k_{0}=\frac{[k, p]}{k}, p_{0}=\frac{[k, p]}{p}$. Then $|a-b| \geqslant \frac{1}{[k, p]}$, as $\left|p_{0} x-k_{0} y\right|$ is a non-zero integer. As
$$
\max \{[k, p] \mid 1 \leqslant k<p \leqslant n-1\}=(n-1)(n-2),
$$
we can say that $m=\min _{\substack{a, b \in M \\ a \neq b}}|a-b| \geqslant \frac{1}{(n-1)(n-2)}$.
To reach this minimum, we seek $x \in\{3,4, \ldots, 2 n-1\}$ and $y \in\{1,2, \ldots, n\}$ for which
$$
\left|\frac{\frac{n(n+1)}{2}-x}{n-2}-\frac{\frac{n(n+1)}{2}-y}{n-1}\right|=\frac{1}{(n-1)(n-2)},
$$
meaning
$$
\left|\frac{n(n+1)}{2}-(n-1) x+(n-2) y\right|=1 .
$$
If $n=2 k$, we can choose $x=k+3$ and $y=2$ and if $n=2 k+1$ we can choose $x=n=2 k+1$ and $y=k$. Therefore, the required minimum is $\frac{1}{(n-1)(n-2)}$.
Comment. For $n \geqslant 5$, the only other possibilities are to take $x=3 k-1, y=2 k-1$ if $n=2 k$ and to take $x=2 k+3, y=k+2$ if $n=2 k+1$. (For $n=3,4$ there are also examples where one of the sets is of size $n$.)
|
\frac{1}{(n-1)(n-2)}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geqslant 3$ be an integer and let
$$
M=\left\{\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}: 1 \leqslant k \leqslant n \text { and } 1 \leqslant a_{1}<\cdots<a_{k} \leqslant n\right\}
$$
be the set of the arithmetic means of the elements of all non-empty subsets of $\{1,2, \ldots, n\}$. Find $\min \{|a-b|: a, b \in M$ with $a \neq b\}$.
## Proposed by Romania
|
We observe that $M$ is composed by rational numbers of the form $a=\frac{x}{k}$, where $1 \leqslant k \leqslant n$. As the arithmetic mean of $1, \ldots, n$ is $\frac{n+1}{2}$, if we look at these rational numbers in their irreducible form, we can say that $1 \leqslant k \leqslant n-1$.
A non-zero difference $|a-b|$ with $a, b \in M$ is then of form
$$
\left|\frac{x}{k}-\frac{y}{p}\right|=\frac{\left|p_{0} x-k_{0} y\right|}{[k, p]}
$$
where $[k, p]$ is the l.c.m. of $k, p$, and $k_{0}=\frac{[k, p]}{k}, p_{0}=\frac{[k, p]}{p}$. Then $|a-b| \geqslant \frac{1}{[k, p]}$, as $\left|p_{0} x-k_{0} y\right|$ is a non-zero integer. As
$$
\max \{[k, p] \mid 1 \leqslant k<p \leqslant n-1\}=(n-1)(n-2),
$$
we can say that $m=\min _{\substack{a, b \in M \\ a \neq b}}|a-b| \geqslant \frac{1}{(n-1)(n-2)}$.
To reach this minimum, we seek $x \in\{3,4, \ldots, 2 n-1\}$ and $y \in\{1,2, \ldots, n\}$ for which
$$
\left|\frac{\frac{n(n+1)}{2}-x}{n-2}-\frac{\frac{n(n+1)}{2}-y}{n-1}\right|=\frac{1}{(n-1)(n-2)},
$$
meaning
$$
\left|\frac{n(n+1)}{2}-(n-1) x+(n-2) y\right|=1 .
$$
If $n=2 k$, we can choose $x=k+3$ and $y=2$ and if $n=2 k+1$ we can choose $x=n=2 k+1$ and $y=k$. Therefore, the required minimum is $\frac{1}{(n-1)(n-2)}$.
Comment. For $n \geqslant 5$, the only other possibilities are to take $x=3 k-1, y=2 k-1$ if $n=2 k$ and to take $x=2 k+3, y=k+2$ if $n=2 k+1$. (For $n=3,4$ there are also examples where one of the sets is of size $n$.)
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN1.",
"solution_match": "\nSolution."
}
|
439e6d91-4fd5-535e-b6da-14b56118fa7d
| 604,254
|
Denote by $\ell(n)$ the largest prime divisor of $n$. Let $a_{n+1}=a_{n}+\ell\left(a_{n}\right)$ be a recursively defined sequence of integers with $a_{1}=2$. Determine all natural numbers $m$ such that there exists some $i \in \mathbb{N}$ with $a_{i}=m^{2}$.
|
We will show that all such numbers are exactly the prime numbers.
Let $p_{1}, p_{2}, \ldots$ be the sequence of prime numbers. We will prove the following:
Claim: Assume $a_{n}=p_{i} p_{i+1}$. Then for each $k=1,2, \ldots, p_{i+2}-p_{i}$ we have that $a_{n+k}=$ $\left(p_{i}+k\right) p_{i+1}$.
Proof. By induction on $k$. Since $\ell\left(a_{n}\right)=p_{i+1}$, then $a_{n+1}=p_{i} p_{i+1}+p_{i+1}=\left(p_{i}+1\right) p_{i+1}$. Assume now that $a_{n+r}=\left(p_{i}+r\right) p_{i+1}$ for some $r<p_{i+2}-p_{i}$. For the inductive step, it is enough to show that $\ell\left(a_{n+r}\right)=p_{i+1}$ as then we would have $a_{n+r}=\left(p_{i}+r\right) p_{i+1}+p_{i+1}=\left(p_{i}+r+1\right) p_{i+1}$. Assume for contradiction that $\ell\left(a_{n+r}\right) \neq p_{i+1}$. Since $p_{i+1} \mid a_{n+r}$, then we must have that $\ell\left(a_{n+r}\right)>p_{i+1}$. Since also $a_{n+r}=\left(p_{i}+r\right) p_{i+1}$, then $\ell\left(p_{i}+r\right)>p_{i+1}$ and therefore $\ell\left(p_{i}+r\right) \geqslant p_{i+2}$. This is impossible as $p_{i}+r<p_{i+2}$.
Since $a_{1}=2, a_{2}=4, a_{3}=6=2 \cdot 3=p_{1} p_{2}$, from the above claim, by induction, we can break up the sequence into pieces of the form $p_{i} p_{i+1},\left(p_{i}+1\right) p_{i+1}, \ldots, p_{i+2} p_{i+1}$ for $i=1,2, \ldots$, together with the initial piece 2,4 .
We immediately see that for each prime $p$, the number $p^{2}$ appears in the sequence. It remains to show that no other square number appears in the sequence.
Assume for contradiction that another square appears in $p_{i} p_{i+1},\left(p_{i}+1\right) p_{i+1}, \ldots, p_{i+2} p_{i+1}$ for some $i$. Since all elements of this piece are multiples of $p_{i+1}$, if a square appears in this sequence, it must be a multiple of $p_{i+1}^{2}$. So the smallest possible square different from $p_{i+1}^{2}$ is $4 p_{i+1}^{2}$. It is enough to show that $4 p_{i+1}^{2}>p_{i+2} p_{i+1}$. This is equivalent to showing that $p_{i+2}<4 p_{i+1}$ which follows from Bertrand's postulate.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Denote by $\ell(n)$ the largest prime divisor of $n$. Let $a_{n+1}=a_{n}+\ell\left(a_{n}\right)$ be a recursively defined sequence of integers with $a_{1}=2$. Determine all natural numbers $m$ such that there exists some $i \in \mathbb{N}$ with $a_{i}=m^{2}$.
|
We will show that all such numbers are exactly the prime numbers.
Let $p_{1}, p_{2}, \ldots$ be the sequence of prime numbers. We will prove the following:
Claim: Assume $a_{n}=p_{i} p_{i+1}$. Then for each $k=1,2, \ldots, p_{i+2}-p_{i}$ we have that $a_{n+k}=$ $\left(p_{i}+k\right) p_{i+1}$.
Proof. By induction on $k$. Since $\ell\left(a_{n}\right)=p_{i+1}$, then $a_{n+1}=p_{i} p_{i+1}+p_{i+1}=\left(p_{i}+1\right) p_{i+1}$. Assume now that $a_{n+r}=\left(p_{i}+r\right) p_{i+1}$ for some $r<p_{i+2}-p_{i}$. For the inductive step, it is enough to show that $\ell\left(a_{n+r}\right)=p_{i+1}$ as then we would have $a_{n+r}=\left(p_{i}+r\right) p_{i+1}+p_{i+1}=\left(p_{i}+r+1\right) p_{i+1}$. Assume for contradiction that $\ell\left(a_{n+r}\right) \neq p_{i+1}$. Since $p_{i+1} \mid a_{n+r}$, then we must have that $\ell\left(a_{n+r}\right)>p_{i+1}$. Since also $a_{n+r}=\left(p_{i}+r\right) p_{i+1}$, then $\ell\left(p_{i}+r\right)>p_{i+1}$ and therefore $\ell\left(p_{i}+r\right) \geqslant p_{i+2}$. This is impossible as $p_{i}+r<p_{i+2}$.
Since $a_{1}=2, a_{2}=4, a_{3}=6=2 \cdot 3=p_{1} p_{2}$, from the above claim, by induction, we can break up the sequence into pieces of the form $p_{i} p_{i+1},\left(p_{i}+1\right) p_{i+1}, \ldots, p_{i+2} p_{i+1}$ for $i=1,2, \ldots$, together with the initial piece 2,4 .
We immediately see that for each prime $p$, the number $p^{2}$ appears in the sequence. It remains to show that no other square number appears in the sequence.
Assume for contradiction that another square appears in $p_{i} p_{i+1},\left(p_{i}+1\right) p_{i+1}, \ldots, p_{i+2} p_{i+1}$ for some $i$. Since all elements of this piece are multiples of $p_{i+1}$, if a square appears in this sequence, it must be a multiple of $p_{i+1}^{2}$. So the smallest possible square different from $p_{i+1}^{2}$ is $4 p_{i+1}^{2}$. It is enough to show that $4 p_{i+1}^{2}>p_{i+2} p_{i+1}$. This is equivalent to showing that $p_{i+2}<4 p_{i+1}$ which follows from Bertrand's postulate.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN2.",
"solution_match": "\nSolution."
}
|
a4e5f6d0-8504-541b-9189-19bd4a58f748
| 604,266
|
Let $n$ be a positive integer. Determine, in terms of $n$, the greatest integer which divides every number of the form $p+1$, where $p \equiv 2 \bmod 3$ is a prime number which does not divide $n$.
## Proposed by Bulgaria
|
Let $k$ be the greatest such integer. We will show that $k=3$ when $n$ is odd and $k=6$ when $n$ is even.
We will say that a number $p$ is nice if $p$ is a prime number of the form $2 \bmod 3$ which does not divide $N$.
Note first that if $3 \mid p+1$ for every nice number $p$ and so $k$ is a multiple of 3 .
If $n$ is odd, then $p=2$ is nice, so we must have $k \mid 3$. From the previous paragraph we get that $k=3$.
If $n$ is even, then $p=2$ is not nice, therefore every nice $p$ is of the form $5 \bmod 6$. So in this case $6 \mid p+1$ for every nice number $p$.
It remains to show that (if $n$ is even then)
(i) There is a nice $p$ such that $4 \nmid p+1$.
(ii) There is a nice $p$ such that $9 \nmid p+1$.
(iii) There is a nice $p$ such that for every prime $q \neq 2,3$ we have that $q \nmid p+1$.
For (i), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 5 \bmod 12$. Any one of them which is larger than $n$ will do.
For (ii), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 2 \bmod 9$. Any one of them which is larger than $n$ will do.
For (iii), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 2 \bmod 3 q$. Any one of them which is larger than $n$ will do.
Remark. In the proposal, the statement of Dirichlet's theorem on Arithmetic Progressions was given as known. Even though this makes the problem fairer we omitted it because we feel that it also makes it easier.
|
3 \text{ when } n \text{ is odd, and } 6 \text{ when } n \text{ is even}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n$ be a positive integer. Determine, in terms of $n$, the greatest integer which divides every number of the form $p+1$, where $p \equiv 2 \bmod 3$ is a prime number which does not divide $n$.
## Proposed by Bulgaria
|
Let $k$ be the greatest such integer. We will show that $k=3$ when $n$ is odd and $k=6$ when $n$ is even.
We will say that a number $p$ is nice if $p$ is a prime number of the form $2 \bmod 3$ which does not divide $N$.
Note first that if $3 \mid p+1$ for every nice number $p$ and so $k$ is a multiple of 3 .
If $n$ is odd, then $p=2$ is nice, so we must have $k \mid 3$. From the previous paragraph we get that $k=3$.
If $n$ is even, then $p=2$ is not nice, therefore every nice $p$ is of the form $5 \bmod 6$. So in this case $6 \mid p+1$ for every nice number $p$.
It remains to show that (if $n$ is even then)
(i) There is a nice $p$ such that $4 \nmid p+1$.
(ii) There is a nice $p$ such that $9 \nmid p+1$.
(iii) There is a nice $p$ such that for every prime $q \neq 2,3$ we have that $q \nmid p+1$.
For (i), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 5 \bmod 12$. Any one of them which is larger than $n$ will do.
For (ii), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 2 \bmod 9$. Any one of them which is larger than $n$ will do.
For (iii), by Dirichlet's theorem on arithmetic progressions, there are infinitely many primes of the form $p \equiv 2 \bmod 3 q$. Any one of them which is larger than $n$ will do.
Remark. In the proposal, the statement of Dirichlet's theorem on Arithmetic Progressions was given as known. Even though this makes the problem fairer we omitted it because we feel that it also makes it easier.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN3.",
"solution_match": "\nSolution."
}
|
6ad3e8d1-741d-51ca-8085-3f9ef0553a7c
| 604,279
|
Can every positive rational number $q$ be written as
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
where $a, b, c, d$ are all positive integers?
Proposed by United Kingdom
|
The answer is yes. Set $a=x^{2023}, b=x^{2021}$ and $c=y^{2024}, d=y^{2022}$ for some integers $x, y$ and let $q=\frac{m}{n}$ in lowest terms. Then we could try to solve
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}=\frac{2 x^{2021 \times 2023}}{2 y^{2022 \times 2024}}=\frac{x^{2021 \times 2023}}{y^{2022 \times 2024}}=\frac{m}{n} .
$$
Consider setting $x=m^{x_{1}} n^{x_{2}}$ and $y=m^{y_{1}} n^{y_{2}}$. Then by considering powers of $m$ and powers of $n$ separately, it would be sufficient to solve the pair of equations
$$
2021 \times 2023 x_{1}-2022 \times 2024 y_{1}=1, \quad \text { and } \quad 2021 \times 2023 x_{2}-2022 \times 2024 y_{2}=-1
$$
We know that these equations have solutions in positive integers so long as $2021 \times 2023$ and $2022 \times 2024$ are coprime. Amongst integers which differ by at most three, the only possible common prime factors are 2 and 3. Clearly 2 is not a common prime factor of the products, nor is 3 , since only one of the four factors is divisible by 3 . So these two integers are coprime, and the equations have solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Can every positive rational number $q$ be written as
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
where $a, b, c, d$ are all positive integers?
Proposed by United Kingdom
|
The answer is yes. Set $a=x^{2023}, b=x^{2021}$ and $c=y^{2024}, d=y^{2022}$ for some integers $x, y$ and let $q=\frac{m}{n}$ in lowest terms. Then we could try to solve
$$
\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}=\frac{2 x^{2021 \times 2023}}{2 y^{2022 \times 2024}}=\frac{x^{2021 \times 2023}}{y^{2022 \times 2024}}=\frac{m}{n} .
$$
Consider setting $x=m^{x_{1}} n^{x_{2}}$ and $y=m^{y_{1}} n^{y_{2}}$. Then by considering powers of $m$ and powers of $n$ separately, it would be sufficient to solve the pair of equations
$$
2021 \times 2023 x_{1}-2022 \times 2024 y_{1}=1, \quad \text { and } \quad 2021 \times 2023 x_{2}-2022 \times 2024 y_{2}=-1
$$
We know that these equations have solutions in positive integers so long as $2021 \times 2023$ and $2022 \times 2024$ are coprime. Amongst integers which differ by at most three, the only possible common prime factors are 2 and 3. Clearly 2 is not a common prime factor of the products, nor is 3 , since only one of the four factors is divisible by 3 . So these two integers are coprime, and the equations have solutions.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN4.",
"solution_match": "\nSolution."
}
|
f7c15e13-0feb-5647-bd2a-61bda774ada7
| 604,289
|
A natural number $n$ is given. Determine all $(n-1)$-tuples of nonnegative integers $a_{1}, a_{2}, \ldots, a_{n-1}$ such that
$$
\left[\frac{m}{2^{n}-1}\right]+\left[\frac{2 m+a_{1}}{2^{n}-1}\right]+\left[\frac{2^{2} m+a_{2}}{2^{n}-1}\right]+\left[\frac{2^{3} m+a_{3}}{2^{n}-1}\right]+\cdots+\left[\frac{2^{n-1} m+a_{n-1}}{2^{n}-1}\right]=m
$$
holds for all $m \in \mathbb{Z}$.
Proposed by Serbia
|
1. We will show that there is a unique such $n$-tuple: $a_{k}=2^{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$.
Write $N=2^{n}-1$ and $f_{k}(x)=\left[\frac{2^{k} x+a_{k}}{N}\right]$ for $k=0,1, \ldots, n-1$, where $a_{0}=0$. Since
$$
\sum_{k=0}^{n-1} f_{k}(m)-\sum_{k=0}^{n-1} f_{k}(m-1)=1
$$
for each $m \in \mathbb{Z}$, there is exactly one $k$ for which $f_{k}(m)=f_{k}(m-1)+1$. We work modulo $N$. The last equality holds if and only if $2^{k} m+a_{k} \in\left\{0,1, \ldots, 2^{k}-1\right\}$. I.e. if and only if
$$
2^{k} m \in\left\{-a_{k}, 1-a_{k}, \ldots, 2^{k}-1-a_{k}\right\}
$$
Multiplying with $2^{n-k}$, and noting that $2^{n} \equiv 1 \bmod N$, we get the following:
For each $m \in \mathbb{Z}$ there is a unique $k \in\{0,1, \ldots, n-1\}$ such that $m \in B_{k}$ (modulo $N$ ) where
$$
B_{k}=\left\{b_{k}, b_{k}+2^{n-k}, \ldots, b_{k}+\left(2^{k}-1\right) 2^{n-k}\right\}
$$
with $b_{k}=-2^{n-k} a_{k}$. Therefore the problem condition is equivalent to $\bigcup_{k=0}^{n-1} B_{k}$ being a partition of $\{0,1, \ldots, N-1\}$.
For a number $b$ and set a $A \subseteq \mathbb{Z}$ we write $b+A=\{b+a: a \in A\}$. With this notation, $B_{n-1}=b_{n-1}+\left\{0,2,4, \ldots, 2^{n}-2\right\}$. The set $B_{n-2}=b_{n-2}+\left\{0,4,8, \ldots, 2^{n}-4\right\}$ is contained in $\overline{B_{n-1}}=b_{n-1}+\left\{1,3, \ldots, 2^{n}-3\right\}$, implying $b_{n-2}, b_{n-2}+2^{n}-4 \in \overline{B_{n-1}}$, which holds only if $b_{n-2} \equiv$ $b_{n-1}+1$. Further, the set $B_{n-3}=b_{n-3}+\left\{0,8,16, \ldots, 2^{n}-8\right\}$ is contained in $\overline{B_{n-1} \cup B_{n-2}}=$ $b_{n-1}+\left\{3,7, \ldots, 2^{n}-5\right\}$, so we must have $b_{n-3} \equiv b_{n-1}+3$. Similarly, $b_{n-4} \equiv b_{n-1}+7$ etc. In general, $b_{n-k} \equiv b_{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$. It follows that $b_{0} \equiv b_{n-1}+2^{n-1}-1$. On the other hand, we have $b_{0}=0$, which gives $b_{n-1} \equiv 1-2^{n-1}$ and therefore $b_{k} \equiv 2^{n-1-k}-2^{n-1}$. Thus $a_{k} \equiv-2^{k} b_{k} \equiv 2^{n+k-1}-2^{n-1} \equiv 2^{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$.
Finally, $\sum_{k} f_{k}(0)=0$ implies $a_{k}<N$ for all $k$, so we conclude that $a_{k}=2^{n-1}+2^{k-1}-1$ for each $k=1,2, \ldots, n-1$.
|
a_{k}=2^{n-1}+2^{k-1}-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A natural number $n$ is given. Determine all $(n-1)$-tuples of nonnegative integers $a_{1}, a_{2}, \ldots, a_{n-1}$ such that
$$
\left[\frac{m}{2^{n}-1}\right]+\left[\frac{2 m+a_{1}}{2^{n}-1}\right]+\left[\frac{2^{2} m+a_{2}}{2^{n}-1}\right]+\left[\frac{2^{3} m+a_{3}}{2^{n}-1}\right]+\cdots+\left[\frac{2^{n-1} m+a_{n-1}}{2^{n}-1}\right]=m
$$
holds for all $m \in \mathbb{Z}$.
Proposed by Serbia
|
1. We will show that there is a unique such $n$-tuple: $a_{k}=2^{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$.
Write $N=2^{n}-1$ and $f_{k}(x)=\left[\frac{2^{k} x+a_{k}}{N}\right]$ for $k=0,1, \ldots, n-1$, where $a_{0}=0$. Since
$$
\sum_{k=0}^{n-1} f_{k}(m)-\sum_{k=0}^{n-1} f_{k}(m-1)=1
$$
for each $m \in \mathbb{Z}$, there is exactly one $k$ for which $f_{k}(m)=f_{k}(m-1)+1$. We work modulo $N$. The last equality holds if and only if $2^{k} m+a_{k} \in\left\{0,1, \ldots, 2^{k}-1\right\}$. I.e. if and only if
$$
2^{k} m \in\left\{-a_{k}, 1-a_{k}, \ldots, 2^{k}-1-a_{k}\right\}
$$
Multiplying with $2^{n-k}$, and noting that $2^{n} \equiv 1 \bmod N$, we get the following:
For each $m \in \mathbb{Z}$ there is a unique $k \in\{0,1, \ldots, n-1\}$ such that $m \in B_{k}$ (modulo $N$ ) where
$$
B_{k}=\left\{b_{k}, b_{k}+2^{n-k}, \ldots, b_{k}+\left(2^{k}-1\right) 2^{n-k}\right\}
$$
with $b_{k}=-2^{n-k} a_{k}$. Therefore the problem condition is equivalent to $\bigcup_{k=0}^{n-1} B_{k}$ being a partition of $\{0,1, \ldots, N-1\}$.
For a number $b$ and set a $A \subseteq \mathbb{Z}$ we write $b+A=\{b+a: a \in A\}$. With this notation, $B_{n-1}=b_{n-1}+\left\{0,2,4, \ldots, 2^{n}-2\right\}$. The set $B_{n-2}=b_{n-2}+\left\{0,4,8, \ldots, 2^{n}-4\right\}$ is contained in $\overline{B_{n-1}}=b_{n-1}+\left\{1,3, \ldots, 2^{n}-3\right\}$, implying $b_{n-2}, b_{n-2}+2^{n}-4 \in \overline{B_{n-1}}$, which holds only if $b_{n-2} \equiv$ $b_{n-1}+1$. Further, the set $B_{n-3}=b_{n-3}+\left\{0,8,16, \ldots, 2^{n}-8\right\}$ is contained in $\overline{B_{n-1} \cup B_{n-2}}=$ $b_{n-1}+\left\{3,7, \ldots, 2^{n}-5\right\}$, so we must have $b_{n-3} \equiv b_{n-1}+3$. Similarly, $b_{n-4} \equiv b_{n-1}+7$ etc. In general, $b_{n-k} \equiv b_{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$. It follows that $b_{0} \equiv b_{n-1}+2^{n-1}-1$. On the other hand, we have $b_{0}=0$, which gives $b_{n-1} \equiv 1-2^{n-1}$ and therefore $b_{k} \equiv 2^{n-1-k}-2^{n-1}$. Thus $a_{k} \equiv-2^{k} b_{k} \equiv 2^{n+k-1}-2^{n-1} \equiv 2^{n-1}+2^{k-1}-1$ for $k=1, \ldots, n-1$.
Finally, $\sum_{k} f_{k}(0)=0$ implies $a_{k}<N$ for all $k$, so we conclude that $a_{k}=2^{n-1}+2^{k-1}-1$ for each $k=1,2, \ldots, n-1$.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN5.",
"solution_match": "\nSolution"
}
|
f16d9dbd-9677-524d-adb1-d997dbc0d908
| 604,300
|
A natural number $n$ is given. Determine all $(n-1)$-tuples of nonnegative integers $a_{1}, a_{2}, \ldots, a_{n-1}$ such that
$$
\left[\frac{m}{2^{n}-1}\right]+\left[\frac{2 m+a_{1}}{2^{n}-1}\right]+\left[\frac{2^{2} m+a_{2}}{2^{n}-1}\right]+\left[\frac{2^{3} m+a_{3}}{2^{n}-1}\right]+\cdots+\left[\frac{2^{n-1} m+a_{n-1}}{2^{n}-1}\right]=m
$$
holds for all $m \in \mathbb{Z}$.
Proposed by Serbia
|
2. We will use the identity
$$
[x]+\left[x+\frac{1}{N}\right]+\left[x+\frac{2}{N}\right]+\cdots+\left[x+\frac{N-1}{N}\right]=[N x]
$$
which holds for every $x \in \mathbb{R}$ and every $N \in \mathbb{N}$. (One can check this by noting that the difference between the two sides of the identity is periodic with period $1 / N$ and that the identity clearly holds for $x \in\left[0, \frac{1}{N}\right)$. )
Writing $a_{0}=0$ and $N=2^{n}-1$ we observe that
$$
m=\sum_{k=0}^{n-1}\left[\frac{2^{k} m+a_{k}}{N}\right]=\sum_{r=0}^{2^{k}-1} \sum_{r=0}^{2^{k}-1}\left[\frac{m+\frac{a_{k}}{2^{k}}}{N}+\frac{r}{2^{k}}\right]=\sum_{k=0}^{n-1} \sum_{r=0}^{2^{k}-1}\left[\frac{m+\frac{a_{k}+r N}{2^{k}}}{N}\right]
$$
It follows that $c_{r, k}=\left[\frac{a_{k}+r N}{2^{k}}\right]$ are all distinct modulo $N$ for $k=0,1, \ldots, n-1$ and $r=$ $0,1, \ldots, 2^{k}-1$. Indeed if two (or more) of them are congruent to $t$, then writing $f(t)$ for the right hand side of $(1)$ we get $1=f(-t)-f(-t-1) \geqslant 2$, a contradiction.
Since $N=2^{n}-1$, then $c_{r, k}=r 2^{n-k}+d_{r, k}$, where $d_{r, k}=\left[\frac{a_{k}-r}{2^{k}}\right]$. Because $c_{0,0}=0$, then $c_{0, k} \neq 0$ for each $k \neq 0$ giving $a_{k} \geqslant 2^{k}$ for each $k \geqslant 1$. Setting $m=0$ in the original equation gives $a_{k}<N$ for each $k$ and so $d_{0, k} \leqslant 2^{n-k}-1$ for each $k$. Furthermore
$$
2^{n-k}-1 \geqslant d_{0, k} \geqslant d_{1, k} \geqslant \cdots \geqslant d_{2^{k}-1, k} \geqslant d_{2^{k}, k}=d_{0, k}-1 \geqslant 0
$$
In particular $0 \leqslant c_{r, k}=r 2^{n-k}+d_{r, k} \leqslant\left(2^{n}-2^{n-k}\right)+\left(2^{n-k}-1\right)=N$. For $k=0,1,2, \ldots, n-1$ define $A_{k}=\left\{c_{r, k}: r=0,1, \ldots, 2^{k}-1\right\}$. From the above, since $A_{0}=\{0\}$, we must have that $A_{1} \cup A_{2} \cup \cdots \cup A_{n-1}=\{1,2, \ldots, N-1\}$.
For a natural number $t$ let $v_{2}(t)$ be as usual the largest exponent such that $2^{v_{2}(t)} \mid t$. Let
$$
f(t)=n-v_{2}(t)-1, \quad g(t)=\frac{t-2^{v_{2}(t)}}{2^{1+v_{2}(t)}}, \quad \text { and } \quad h(t)=2^{f(t)}-1-g(t)
$$
Note that $f(t)$ uniquely determines $v_{2}(t)$ and together with $g(t)$ they uniquely determine $t$. Similarly $h(t)$ and $g(t)$ uniquely determine $t$.
Claim. For each $t \in\left\{1,2, \ldots, 2^{n-1}-1\right\}$ we have:
(i) $d_{g(t), f(t)}=2^{v_{2}(t)}$,
(ii) $d_{h(t), f(t)}=2^{v_{2}(t)}-1$,
(iii) $c_{g(t), f(t)}=t$,
(iv) $c_{h(t), f(t)}=N-t$.
Proof of Claim. We proceed by induction on $t$. For $t=1$ we have $v_{2}(1)=0, f(1)=$ $n-1, g(1)=0$ and $h(1)=2^{n-1}-1$. From (2) we have $1 \geqslant d_{0, n-1}$ and $d_{0, n-1}-1 \geqslant 0$ proving (i). Also, $c_{g(1), f(1)}=c_{0, n-1}=d_{0, n-1}=1$ proving (iii). From (2) we have $1 \geqslant d_{2^{n-1}-1, n-1} \geqslant 0$. But $c_{2^{n-1}-1, n-1}=2^{n}-2+d_{2^{n-1}-1, n-1}=N-1+d_{2^{n-1}-1, n-1}$. Since $c_{2^{n-1}-1, n-1} \leqslant N-1$ we deduce both (ii) and (iv).
Assume now that the result is true for $t=s-1$. We will prove the result for $t=s$.
Case 1: If $s-1=2 u$ is even, then $v_{2}(s)=0$, so $f(s)=n-1, g(s)=u$ and $h(s)=2^{n-1}-1-u$.
By the induction hypothesis, since all the $c_{r, k}$ 's are distinct, we must have
$$
s \leqslant c_{g(s), f(s)}=2 u+d_{g(s), f(s)}=s-1+d_{g(s), f(s)}
$$
and
$$
N-s \geqslant c_{h(s), f(s)}=2^{n}-2-2 u+d_{h(s), f(s)}=N-s+d_{h(s), f(s)}
$$
From the above we must have $d_{g(s), f(s)} \geqslant 1$ and $d_{h(s), f(s)} \leqslant 0$. But from (2) any two $d_{r, k}$ 's for fixed $k$ differ by at most 1 . This can only be achieved if we have equalities everywhere proving (i)-(iv).
Case 2: If $s-1=2 u+1$ is odd, then we write $s=2 u+2=2^{v} w$ for some odd $w$. Then $v_{2}(s)=v$ and so $k=f(s)=n-1-v$ and $r=g(s)=(w-1) / 2$. Also $h(s)=2^{k}-1-r$. By the induction hypothesis we must have
$$
s \leqslant c_{r, k}=r 2^{n-k}+d_{r, k}=2^{v}(w-1)+d_{r, k}=s-2^{v}+d_{r, k}
$$
and
$$
\begin{aligned}
N-s \geqslant c_{h(s), k} & =\left(2^{k}-1-r\right) 2^{n-k}+d_{h(s), k} \\
& =2^{n}-2^{v+1}-s+2^{v}+d_{h(s), k} \\
& =N+1-s-2^{v}+d_{h(s), k}
\end{aligned}
$$
From the above we must have $d_{r, k} \geqslant 2^{v}$ and $d_{h(s), k} \leqslant 2^{v}-1$. As in Case 1 we must have equalities everywhere proving (i)-(iv).
For $t=2^{n-1}-2^{n-k-1}$ we have $v_{2}(t)=n-k-1, f(t)=k, g(t)=2^{k-1}-1$ and $h(t)=$ $2^{k}-1-\left(2^{k-1}-1\right)=2^{k-1}$. Thus from (ii) and (iv) we get
$$
\left[\frac{a_{k}-\left(2^{k-1}-1\right)}{2^{k}}\right]=2^{n-k-1} \quad \text { and } \quad\left[\frac{a_{k}-2^{k-1}}{2^{k}}\right]=2^{n-k-1}-1 .
$$
This is only possible if $a^{k}=2^{k} \cdot 2^{n-k-1}+\left(2^{k-1}-1\right)=2^{n-1}+2^{k-1}-1$ as required.
|
a_{k}=2^{n-1}+2^{k-1}-1
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
A natural number $n$ is given. Determine all $(n-1)$-tuples of nonnegative integers $a_{1}, a_{2}, \ldots, a_{n-1}$ such that
$$
\left[\frac{m}{2^{n}-1}\right]+\left[\frac{2 m+a_{1}}{2^{n}-1}\right]+\left[\frac{2^{2} m+a_{2}}{2^{n}-1}\right]+\left[\frac{2^{3} m+a_{3}}{2^{n}-1}\right]+\cdots+\left[\frac{2^{n-1} m+a_{n-1}}{2^{n}-1}\right]=m
$$
holds for all $m \in \mathbb{Z}$.
Proposed by Serbia
|
2. We will use the identity
$$
[x]+\left[x+\frac{1}{N}\right]+\left[x+\frac{2}{N}\right]+\cdots+\left[x+\frac{N-1}{N}\right]=[N x]
$$
which holds for every $x \in \mathbb{R}$ and every $N \in \mathbb{N}$. (One can check this by noting that the difference between the two sides of the identity is periodic with period $1 / N$ and that the identity clearly holds for $x \in\left[0, \frac{1}{N}\right)$. )
Writing $a_{0}=0$ and $N=2^{n}-1$ we observe that
$$
m=\sum_{k=0}^{n-1}\left[\frac{2^{k} m+a_{k}}{N}\right]=\sum_{r=0}^{2^{k}-1} \sum_{r=0}^{2^{k}-1}\left[\frac{m+\frac{a_{k}}{2^{k}}}{N}+\frac{r}{2^{k}}\right]=\sum_{k=0}^{n-1} \sum_{r=0}^{2^{k}-1}\left[\frac{m+\frac{a_{k}+r N}{2^{k}}}{N}\right]
$$
It follows that $c_{r, k}=\left[\frac{a_{k}+r N}{2^{k}}\right]$ are all distinct modulo $N$ for $k=0,1, \ldots, n-1$ and $r=$ $0,1, \ldots, 2^{k}-1$. Indeed if two (or more) of them are congruent to $t$, then writing $f(t)$ for the right hand side of $(1)$ we get $1=f(-t)-f(-t-1) \geqslant 2$, a contradiction.
Since $N=2^{n}-1$, then $c_{r, k}=r 2^{n-k}+d_{r, k}$, where $d_{r, k}=\left[\frac{a_{k}-r}{2^{k}}\right]$. Because $c_{0,0}=0$, then $c_{0, k} \neq 0$ for each $k \neq 0$ giving $a_{k} \geqslant 2^{k}$ for each $k \geqslant 1$. Setting $m=0$ in the original equation gives $a_{k}<N$ for each $k$ and so $d_{0, k} \leqslant 2^{n-k}-1$ for each $k$. Furthermore
$$
2^{n-k}-1 \geqslant d_{0, k} \geqslant d_{1, k} \geqslant \cdots \geqslant d_{2^{k}-1, k} \geqslant d_{2^{k}, k}=d_{0, k}-1 \geqslant 0
$$
In particular $0 \leqslant c_{r, k}=r 2^{n-k}+d_{r, k} \leqslant\left(2^{n}-2^{n-k}\right)+\left(2^{n-k}-1\right)=N$. For $k=0,1,2, \ldots, n-1$ define $A_{k}=\left\{c_{r, k}: r=0,1, \ldots, 2^{k}-1\right\}$. From the above, since $A_{0}=\{0\}$, we must have that $A_{1} \cup A_{2} \cup \cdots \cup A_{n-1}=\{1,2, \ldots, N-1\}$.
For a natural number $t$ let $v_{2}(t)$ be as usual the largest exponent such that $2^{v_{2}(t)} \mid t$. Let
$$
f(t)=n-v_{2}(t)-1, \quad g(t)=\frac{t-2^{v_{2}(t)}}{2^{1+v_{2}(t)}}, \quad \text { and } \quad h(t)=2^{f(t)}-1-g(t)
$$
Note that $f(t)$ uniquely determines $v_{2}(t)$ and together with $g(t)$ they uniquely determine $t$. Similarly $h(t)$ and $g(t)$ uniquely determine $t$.
Claim. For each $t \in\left\{1,2, \ldots, 2^{n-1}-1\right\}$ we have:
(i) $d_{g(t), f(t)}=2^{v_{2}(t)}$,
(ii) $d_{h(t), f(t)}=2^{v_{2}(t)}-1$,
(iii) $c_{g(t), f(t)}=t$,
(iv) $c_{h(t), f(t)}=N-t$.
Proof of Claim. We proceed by induction on $t$. For $t=1$ we have $v_{2}(1)=0, f(1)=$ $n-1, g(1)=0$ and $h(1)=2^{n-1}-1$. From (2) we have $1 \geqslant d_{0, n-1}$ and $d_{0, n-1}-1 \geqslant 0$ proving (i). Also, $c_{g(1), f(1)}=c_{0, n-1}=d_{0, n-1}=1$ proving (iii). From (2) we have $1 \geqslant d_{2^{n-1}-1, n-1} \geqslant 0$. But $c_{2^{n-1}-1, n-1}=2^{n}-2+d_{2^{n-1}-1, n-1}=N-1+d_{2^{n-1}-1, n-1}$. Since $c_{2^{n-1}-1, n-1} \leqslant N-1$ we deduce both (ii) and (iv).
Assume now that the result is true for $t=s-1$. We will prove the result for $t=s$.
Case 1: If $s-1=2 u$ is even, then $v_{2}(s)=0$, so $f(s)=n-1, g(s)=u$ and $h(s)=2^{n-1}-1-u$.
By the induction hypothesis, since all the $c_{r, k}$ 's are distinct, we must have
$$
s \leqslant c_{g(s), f(s)}=2 u+d_{g(s), f(s)}=s-1+d_{g(s), f(s)}
$$
and
$$
N-s \geqslant c_{h(s), f(s)}=2^{n}-2-2 u+d_{h(s), f(s)}=N-s+d_{h(s), f(s)}
$$
From the above we must have $d_{g(s), f(s)} \geqslant 1$ and $d_{h(s), f(s)} \leqslant 0$. But from (2) any two $d_{r, k}$ 's for fixed $k$ differ by at most 1 . This can only be achieved if we have equalities everywhere proving (i)-(iv).
Case 2: If $s-1=2 u+1$ is odd, then we write $s=2 u+2=2^{v} w$ for some odd $w$. Then $v_{2}(s)=v$ and so $k=f(s)=n-1-v$ and $r=g(s)=(w-1) / 2$. Also $h(s)=2^{k}-1-r$. By the induction hypothesis we must have
$$
s \leqslant c_{r, k}=r 2^{n-k}+d_{r, k}=2^{v}(w-1)+d_{r, k}=s-2^{v}+d_{r, k}
$$
and
$$
\begin{aligned}
N-s \geqslant c_{h(s), k} & =\left(2^{k}-1-r\right) 2^{n-k}+d_{h(s), k} \\
& =2^{n}-2^{v+1}-s+2^{v}+d_{h(s), k} \\
& =N+1-s-2^{v}+d_{h(s), k}
\end{aligned}
$$
From the above we must have $d_{r, k} \geqslant 2^{v}$ and $d_{h(s), k} \leqslant 2^{v}-1$. As in Case 1 we must have equalities everywhere proving (i)-(iv).
For $t=2^{n-1}-2^{n-k-1}$ we have $v_{2}(t)=n-k-1, f(t)=k, g(t)=2^{k-1}-1$ and $h(t)=$ $2^{k}-1-\left(2^{k-1}-1\right)=2^{k-1}$. Thus from (ii) and (iv) we get
$$
\left[\frac{a_{k}-\left(2^{k-1}-1\right)}{2^{k}}\right]=2^{n-k-1} \quad \text { and } \quad\left[\frac{a_{k}-2^{k-1}}{2^{k}}\right]=2^{n-k-1}-1 .
$$
This is only possible if $a^{k}=2^{k} \cdot 2^{n-k-1}+\left(2^{k-1}-1\right)=2^{n-1}+2^{k-1}-1$ as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN5.",
"solution_match": "\nSolution"
}
|
f16d9dbd-9677-524d-adb1-d997dbc0d908
| 604,300
|
Let $a, b$ and $c$ be positive integers satisfying the equation $(a, b)+[a, b]=2021^{c}$. If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
## Proposed by Serbia
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5 .
$$
So 5 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1 .
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ and $c$ be positive integers satisfying the equation $(a, b)+[a, b]=2021^{c}$. If $|a-b|$ is a prime number, prove that the number $(a+b)^{2}+4$ is composite.
## Proposed by Serbia
|
We write $p=|a-b|$ and assume for contradiction that $q=(a+b)^{2}+4$ is a prime number.
Since $(a, b) \mid[a, b]$, we have that $(a, b) \mid 2021^{c}$. As $(a, b)$ also divides $p=|a-b|$, it follows that $(a, b) \in\{1,43,47\}$. We will consider all 3 cases separately:
(1) If $(a, b)=1$, then $1+a b=2021^{c}$, and therefore
$$
q=(a+b)^{2}+4=(a-b)^{2}+4(1+a b)=p^{2}+4 \cdot 2021^{c} .
$$
(a) Suppose $c$ is even. Since $q \equiv 1 \bmod 4$, it can be represented uniquely (up to order) as a sum of two (non-negative) squares. But (1) gives potentially two such representations so in order to have uniqueness we must have $p=2$. But then $4 \mid q$ a contradiction.
(b) If $c$ is odd then $a b=2021^{c}-1 \equiv 1 \bmod 3$. Thus $a \equiv b \bmod 3$ implying that $p=|a-b| \equiv 0 \bmod 3$. Therefore $p=3$. Without loss of generality $b=a+3$. Then $2021^{c}=a b+1=a^{2}+3 a+1$ and so
$$
(2 a+3)^{2}=4 a^{2}+12 a+9=4 \cdot 2021^{c}+5 .
$$
So 5 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{5}{47}\right)=\left(\frac{47}{5}\right)=\left(\frac{2}{5}\right)=-1 .
$$
(2) If $(a, b)=43$, then $p=|a-b|=43$ and we may assume that $a=43 k$ and $b=43(k+1)$, for some $k \in \mathbb{N}$. Then $2021^{c}=43+43 k(k+1)$ giving that
$$
(2 k+1)^{2}=4 k^{2}+4 k+4-3=4 \cdot 43^{c-1} \cdot 47-3 .
$$
So -3 is a quadratic residue modulo 47 , a contradiction as
$$
\left(\frac{-3}{47}\right)=\left(\frac{-1}{47}\right)\left(\frac{3}{47}\right)=\left(\frac{47}{3}\right)=\left(\frac{2}{3}\right)=-1 .
$$
(3) If $(a, b)=47$ then analogously there is a $k \in \mathbb{N}$ such that
$$
(2 k+1)^{2}=4 \cdot 43^{c} \cdot 47^{c-1}-3
$$
If $c>1$ then we get a contradiction in exactly the same way as in (2). If $c=1$ then $(2 k+1)^{2}=169$ giving $k=6$. This implies that $a+b=47 \cdot 6+47 \cdot 7=47 \cdot 13 \equiv 1 \bmod 5$. Thus $q=(a+b)^{2}+4 \equiv 0 \bmod 5$, a contradiction.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN6.",
"solution_match": "\nSolution."
}
|
6437f917-6b32-5520-8f50-32d856b8dc36
| 604,320
|
A super-integer triangle is defined to be a triangle whose lengths of all sides and at least one height are positive integers. We will deem certain positive integer numbers to be good with the condition that if the lengths of two sides of a super-integer triangle are two (not necessarily different) good numbers, then the length of the remaining side is also a good number. Let 5 be a good number. Prove that all integers larger than 2 are good numbers.
## Proposed by Serbia
|
Evidently, all right-angle triangles with integer sides are super-integer triangles. We will use the following notation $(a, b, c\{h\})$ to denote a super-integer triangle whose sides are $a$, $b$ and $c$ and the height of integer length is $h$. The height will be written in curly brackets next to the corresponding side and it will be omitted for right-angled triangles. It also follows that if $(a, b, c)$ is an super-integer triangle, then so is $(k a, k b, k c)$, where $k$ is a positive integer.
Note. In all cases of right-angled triangles one can check directly that they are right-angled by Pythagoras' Theorem or use the standard result that $\left(d\left(m^{2}-n^{2}\right), 2 d m n, d\left(m^{2}+n^{2}\right)\right)$ is a right-angled triangle. For non-right angled triangled we will use Heron's formula that the area of the triangle is $\sqrt{s(s-a)(s-b)(s-c)}$ where $s$ is the semiperimeter. For the triangle to be super-integer we need that $s(s-a)(s-b)(s-c)$ is a perfect square, say $s=m^{2}$, and that $2 m$ is a multiple of $a$ or $b$ or $c$. We will only make implicit use of the above.
From $(5,5,6\{4\})$ and $(5,5,8\{3\})$ it follows that 6 and 8 are good. From $(6,8,10)$ it then follows that 10 is also good.
It thus follows if $a$ is good that $2 a$ is also good. Indeed consider a sequence of super-integer triangles showing that if 5 is good then $a$ is good. Then the sequence of super-integer triangles of double the size of their edges show that since 10 is good then $2 a$ is good.
It easily follows that $12,16,20$ and 24 are good. From $(5,12,13)$ it follows that 13 and therefore also 26 are good. From $(11\{12\}, 13,20)$ and $(21\{12\}, 13,20)$ it follows that 11 and 21 are good. From $(20,21,29)$ it follows that 29 is good. From $(6\{20\}, 25,29)$ it follows that 25 is good.
We will say that a positive integer is nice if it is either good or equal to 1 or 2 .
Claim 1. If $a$ is good and $b$ is nice then $a b$ is good.
Proof of Claim. The claim is trivial if $b=1$ and we already proved the case $b=2$. So assume that $b$ is good. Pick a sequence of super-integer triangles which shows that if 5 is good then $b$ is good. Then the sequence of super-integer triangles 5 times the size of their edges shows that since 25 is good then $5 b$ is also good. Now pick a sequence of super-integer triangles which shows that if 5 is good then $b$ is good. Then the sequence of super-integer triangles $b$ times the size of their edges shows that since $5 a$ is good then $a b$ is also good.
Next, from $(15,20,25)$ and $(7,24,25)$ we get that 15,7 and therefore 14 are good. From $(9,12,15)$ and $(8,15,17)$ we get that 9,17 and therefore 18 are good and finally from $(3\{24\}, 25,26)$ and then $(3,4,5)$ we get that 3 and 4 are good.
We now have that all integers from 3 to 18 are good. To prove that the remaining integers larger than 18 are good, we will proceed by strong induction. Assume that all integers from 3 to $n-1$ are good for $n \geqslant 19$.
Case 1. If $n=2 m$ is even, then $3 \leqslant m \leqslant n-1$ so $m$ is good. By Claim $1, n=2 m$ is also good.
Case 2. If $n$ is odd and composite, say $n=a b$, with $a, b>1$, then $3 \leqslant a, b \leqslant n-1$ so $a, b$ are good. By Claim 1, $n=a b$ is also good.
Case 3. If $n$ is an odd prime of the form $4 k+1$, then by Fermat sum of two squares theorem we can write $n=a^{2}+b^{2}$. We may assume $a>b .(a \neq b$ as $n$ is prime.) Consider the triangle $\left(a^{2}-b^{2}, 2 a b, a^{2}+b^{2}\right)$. This is a super-integer triangle since it is a right-angled triangle. We have $3 \leqslant a^{2}-b^{2} \leqslant n-1$ so $a^{2}-b^{2}$ is good. We also have $3 \leqslant 2 a b<a^{2}+b^{2}=n$ so $2 a b$ is also good. Thus $n=a^{2}+b^{2}$ is good as well.
Case 4. Assume $n$ is an odd prime of the form $4 k+3$. Note that $4 k+4$ is good by Case 1 as $2 k+2<4 k+3$. We also have that $4 k+5$ is good either by Case 2 (if it is composite) or by Case 3 (if it is prime) except if $4 k+5$ is a prime equal to $a^{2}+1$. (Because in this case, to use Case 3 we would need that $a^{2}-1=n$ is good which is what we are trying to prove. But in this exceptional case $n=a^{2}-1=(a-1)(a+1)$ is not prime.
We will make use of the following Claim:
Claim 2. Let $a, b, \ell$ be positive integers such that $\ell>1$ and $a \neq b$. If $\ell-1,|a-b|, a, b$ are nice, and $\ell, a+b, a^{2} \ell+b^{2}$ are good, then $a^{2} \ell^{2}+b^{2}$ is good.
Proof of Claim. By Claim 1, the numbers $\left|a^{2}-b^{2}\right|=|a-b|(a+b)$ and $2 a b$ are good. From the right-angled triangle ( $2 a b,\left|a^{2}-b^{2}\right|, a^{2}+b^{2}$ ) it follows that $a^{2}+b^{2}$ is good. So by Claim $1 \ell\left(a^{2}+b^{2}\right)$ is good. By Claim $1(\ell-1)\left(a^{2} \ell+b^{2}\right)$ is also good. Finally, from the triangle $\left((\ell-1)\left(a^{2} \ell+b^{2}\right)\{2 \ell a b\}, \ell\left(a^{2}+b^{2}\right), a^{2} \ell^{2}+b^{2}\right)$, we get that $a^{2} \ell^{2}+b^{2}$ is good.
From Claim 2 with $a=2, b=1$ and $\ell=k+1$ to obtain that
$$
2^{2}(k+1)^{2}+1^{2}=4 k^{2}+8 k+5=4(k+1)+(2 k+1)^{2}
$$
is good. From Claim 2 with $a=2, b=2 k+1$ and $\ell=k+1$ we obtain that
$$
2^{2}(k+1)^{2}+(2 k+1)^{2}=(2 k+2)^{2}+(2 k+1)^{2}
$$
is good. Since from Claim $1,2(2 k+1)(2 k+2)$ is good, then from the right-angled triangle $\left(4 k+3,2(2 k+1)(2 k+2),(2 k+2)^{2}+(2 k+1)^{2}\right)$ we finally deduce that $4 k+3$ is good as required.
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
A super-integer triangle is defined to be a triangle whose lengths of all sides and at least one height are positive integers. We will deem certain positive integer numbers to be good with the condition that if the lengths of two sides of a super-integer triangle are two (not necessarily different) good numbers, then the length of the remaining side is also a good number. Let 5 be a good number. Prove that all integers larger than 2 are good numbers.
## Proposed by Serbia
|
Evidently, all right-angle triangles with integer sides are super-integer triangles. We will use the following notation $(a, b, c\{h\})$ to denote a super-integer triangle whose sides are $a$, $b$ and $c$ and the height of integer length is $h$. The height will be written in curly brackets next to the corresponding side and it will be omitted for right-angled triangles. It also follows that if $(a, b, c)$ is an super-integer triangle, then so is $(k a, k b, k c)$, where $k$ is a positive integer.
Note. In all cases of right-angled triangles one can check directly that they are right-angled by Pythagoras' Theorem or use the standard result that $\left(d\left(m^{2}-n^{2}\right), 2 d m n, d\left(m^{2}+n^{2}\right)\right)$ is a right-angled triangle. For non-right angled triangled we will use Heron's formula that the area of the triangle is $\sqrt{s(s-a)(s-b)(s-c)}$ where $s$ is the semiperimeter. For the triangle to be super-integer we need that $s(s-a)(s-b)(s-c)$ is a perfect square, say $s=m^{2}$, and that $2 m$ is a multiple of $a$ or $b$ or $c$. We will only make implicit use of the above.
From $(5,5,6\{4\})$ and $(5,5,8\{3\})$ it follows that 6 and 8 are good. From $(6,8,10)$ it then follows that 10 is also good.
It thus follows if $a$ is good that $2 a$ is also good. Indeed consider a sequence of super-integer triangles showing that if 5 is good then $a$ is good. Then the sequence of super-integer triangles of double the size of their edges show that since 10 is good then $2 a$ is good.
It easily follows that $12,16,20$ and 24 are good. From $(5,12,13)$ it follows that 13 and therefore also 26 are good. From $(11\{12\}, 13,20)$ and $(21\{12\}, 13,20)$ it follows that 11 and 21 are good. From $(20,21,29)$ it follows that 29 is good. From $(6\{20\}, 25,29)$ it follows that 25 is good.
We will say that a positive integer is nice if it is either good or equal to 1 or 2 .
Claim 1. If $a$ is good and $b$ is nice then $a b$ is good.
Proof of Claim. The claim is trivial if $b=1$ and we already proved the case $b=2$. So assume that $b$ is good. Pick a sequence of super-integer triangles which shows that if 5 is good then $b$ is good. Then the sequence of super-integer triangles 5 times the size of their edges shows that since 25 is good then $5 b$ is also good. Now pick a sequence of super-integer triangles which shows that if 5 is good then $b$ is good. Then the sequence of super-integer triangles $b$ times the size of their edges shows that since $5 a$ is good then $a b$ is also good.
Next, from $(15,20,25)$ and $(7,24,25)$ we get that 15,7 and therefore 14 are good. From $(9,12,15)$ and $(8,15,17)$ we get that 9,17 and therefore 18 are good and finally from $(3\{24\}, 25,26)$ and then $(3,4,5)$ we get that 3 and 4 are good.
We now have that all integers from 3 to 18 are good. To prove that the remaining integers larger than 18 are good, we will proceed by strong induction. Assume that all integers from 3 to $n-1$ are good for $n \geqslant 19$.
Case 1. If $n=2 m$ is even, then $3 \leqslant m \leqslant n-1$ so $m$ is good. By Claim $1, n=2 m$ is also good.
Case 2. If $n$ is odd and composite, say $n=a b$, with $a, b>1$, then $3 \leqslant a, b \leqslant n-1$ so $a, b$ are good. By Claim 1, $n=a b$ is also good.
Case 3. If $n$ is an odd prime of the form $4 k+1$, then by Fermat sum of two squares theorem we can write $n=a^{2}+b^{2}$. We may assume $a>b .(a \neq b$ as $n$ is prime.) Consider the triangle $\left(a^{2}-b^{2}, 2 a b, a^{2}+b^{2}\right)$. This is a super-integer triangle since it is a right-angled triangle. We have $3 \leqslant a^{2}-b^{2} \leqslant n-1$ so $a^{2}-b^{2}$ is good. We also have $3 \leqslant 2 a b<a^{2}+b^{2}=n$ so $2 a b$ is also good. Thus $n=a^{2}+b^{2}$ is good as well.
Case 4. Assume $n$ is an odd prime of the form $4 k+3$. Note that $4 k+4$ is good by Case 1 as $2 k+2<4 k+3$. We also have that $4 k+5$ is good either by Case 2 (if it is composite) or by Case 3 (if it is prime) except if $4 k+5$ is a prime equal to $a^{2}+1$. (Because in this case, to use Case 3 we would need that $a^{2}-1=n$ is good which is what we are trying to prove. But in this exceptional case $n=a^{2}-1=(a-1)(a+1)$ is not prime.
We will make use of the following Claim:
Claim 2. Let $a, b, \ell$ be positive integers such that $\ell>1$ and $a \neq b$. If $\ell-1,|a-b|, a, b$ are nice, and $\ell, a+b, a^{2} \ell+b^{2}$ are good, then $a^{2} \ell^{2}+b^{2}$ is good.
Proof of Claim. By Claim 1, the numbers $\left|a^{2}-b^{2}\right|=|a-b|(a+b)$ and $2 a b$ are good. From the right-angled triangle ( $2 a b,\left|a^{2}-b^{2}\right|, a^{2}+b^{2}$ ) it follows that $a^{2}+b^{2}$ is good. So by Claim $1 \ell\left(a^{2}+b^{2}\right)$ is good. By Claim $1(\ell-1)\left(a^{2} \ell+b^{2}\right)$ is also good. Finally, from the triangle $\left((\ell-1)\left(a^{2} \ell+b^{2}\right)\{2 \ell a b\}, \ell\left(a^{2}+b^{2}\right), a^{2} \ell^{2}+b^{2}\right)$, we get that $a^{2} \ell^{2}+b^{2}$ is good.
From Claim 2 with $a=2, b=1$ and $\ell=k+1$ to obtain that
$$
2^{2}(k+1)^{2}+1^{2}=4 k^{2}+8 k+5=4(k+1)+(2 k+1)^{2}
$$
is good. From Claim 2 with $a=2, b=2 k+1$ and $\ell=k+1$ we obtain that
$$
2^{2}(k+1)^{2}+(2 k+1)^{2}=(2 k+2)^{2}+(2 k+1)^{2}
$$
is good. Since from Claim $1,2(2 k+1)(2 k+2)$ is good, then from the right-angled triangle $\left(4 k+3,2(2 k+1)(2 k+2),(2 k+2)^{2}+(2 k+1)^{2}\right)$ we finally deduce that $4 k+3$ is good as required.
|
{
"resource_path": "Balkan_Shortlist/segmented/en-2021_bmo_shortlist.jsonl",
"problem_match": "\nN7.",
"solution_match": "\nSolution."
}
|
71b28c41-f7ae-5f60-bcc0-0d032aed8a01
| 604,331
|
Let $K$ be a point inside the triangle $A B C$. Let $M$ and $N$ be points such that $M$ and $K$ are on opposite sides of the line $A B$, and $N$ and $K$ are on opposite sides of the line $B C$. Assume that
$$
\angle M A B=\angle M B A=\angle N B C=\angle N C B=\angle K A C=\angle K C A .
$$
Show that $M B N K$ is a parallelogram.
|
Denote $\angle M A B=\angle M B A=\cdots=\alpha$. Then
$$
\angle M A K=\alpha+(\angle B A C-\alpha)=\angle B A C,
$$
$\frac{|A M|}{|A B|}=\frac{1}{2 \cos \alpha}$ and $\frac{|A K|}{|A C|}=\frac{1}{2 \cos \alpha}$ (see Figure 1). Hence the triangles $M A K$ and $B A C$ are similar, implying $|M K|=\frac{|B C|}{2 \cos \alpha}$. Since $|B N|=\frac{|B C|}{2 \cos \alpha}$, we have $|M K|=|B N|$. Similarly we can show that $|B M|=|N K|$, and the result follows.
Figure 1
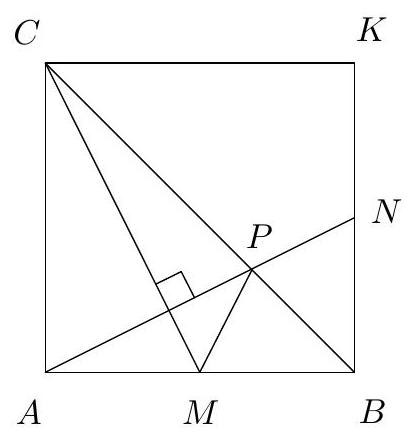
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $K$ be a point inside the triangle $A B C$. Let $M$ and $N$ be points such that $M$ and $K$ are on opposite sides of the line $A B$, and $N$ and $K$ are on opposite sides of the line $B C$. Assume that
$$
\angle M A B=\angle M B A=\angle N B C=\angle N C B=\angle K A C=\angle K C A .
$$
Show that $M B N K$ is a parallelogram.
|
Denote $\angle M A B=\angle M B A=\cdots=\alpha$. Then
$$
\angle M A K=\alpha+(\angle B A C-\alpha)=\angle B A C,
$$
$\frac{|A M|}{|A B|}=\frac{1}{2 \cos \alpha}$ and $\frac{|A K|}{|A C|}=\frac{1}{2 \cos \alpha}$ (see Figure 1). Hence the triangles $M A K$ and $B A C$ are similar, implying $|M K|=\frac{|B C|}{2 \cos \alpha}$. Since $|B N|=\frac{|B C|}{2 \cos \alpha}$, we have $|M K|=|B N|$. Similarly we can show that $|B M|=|N K|$, and the result follows.

Figure 1

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\n1."
}
|
fb639366-f078-5864-8494-c43ff23e77db
| 240,303
|
Given an isosceles triangle $A B C$ with $\angle A=90^{\circ}$. Let $M$ be the midpoint of $A B$. The line passing through $A$ and perpendicular to $C M$ intersects the side $B C$ at $P$. Prove that $\angle A M C=\angle B M P$.
|
Choose the point $K$ such that $A B K C$ is a square. Let $N$ be the point of intersection of $A P$ and $B K$ (see Figure 2). Since the lines $A N$ and $C M$ are perpendicular, $N$ is the midpoint of $B K$. Moreover, triangles $A M C$ and $B N A$ are congruent, which gives
$$
\angle A M C=\angle B N A
$$
Since $|B M|=|B N|$ and $\angle M B P=\angle N B P$, it follows that triangles $M B P$ and $N B P$ are congruent. This implies that
$$
\angle B M P=\angle B N P
$$
Combining (1) ja (2) yields the required equality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given an isosceles triangle $A B C$ with $\angle A=90^{\circ}$. Let $M$ be the midpoint of $A B$. The line passing through $A$ and perpendicular to $C M$ intersects the side $B C$ at $P$. Prove that $\angle A M C=\angle B M P$.
|
Choose the point $K$ such that $A B K C$ is a square. Let $N$ be the point of intersection of $A P$ and $B K$ (see Figure 2). Since the lines $A N$ and $C M$ are perpendicular, $N$ is the midpoint of $B K$. Moreover, triangles $A M C$ and $B N A$ are congruent, which gives
$$
\angle A M C=\angle B N A
$$
Since $|B M|=|B N|$ and $\angle M B P=\angle N B P$, it follows that triangles $M B P$ and $N B P$ are congruent. This implies that
$$
\angle B M P=\angle B N P
$$
Combining (1) ja (2) yields the required equality.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
5d4ea946-e0b1-52f5-b41c-067d59fa6bc7
| 240,313
|
Given a triangle $A B C$ with $\angle A=90^{\circ}$ and $|A B| \neq|A C|$. The points $D, E, F$ lie on the sides $B C, C A, A B$, respectively, in such a way that $A F D E$ is a square. Prove that the line $B C$, the line $F E$ and the line tangent at the point $A$ to the circumcircle of the triangle $A B C$ intersect in one point.
|
Let $B C$ and $F E$ meet at $P$ (see Figure 3 ). It suffices to show that the line $A P$ is tangent to the circumcircle of the triangle $A B C$.
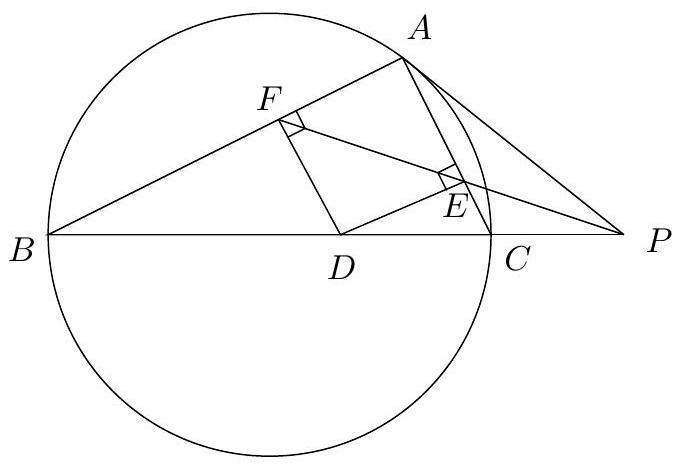
Figure 3
Since $F E$ is the axis of symmetry of the square $A F D E$, we have $\angle A P E=\angle B P F$. Moreover, $\angle A E P=135^{\circ}=\angle B F P$. Hence triangles $A P E$ and $B P F$ are similar, and $\angle C A P=\angle A B C$, i.e. the line $A P$ is tangent to the circumcircle of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$ with $\angle A=90^{\circ}$ and $|A B| \neq|A C|$. The points $D, E, F$ lie on the sides $B C, C A, A B$, respectively, in such a way that $A F D E$ is a square. Prove that the line $B C$, the line $F E$ and the line tangent at the point $A$ to the circumcircle of the triangle $A B C$ intersect in one point.
|
Let $B C$ and $F E$ meet at $P$ (see Figure 3 ). It suffices to show that the line $A P$ is tangent to the circumcircle of the triangle $A B C$.

Figure 3
Since $F E$ is the axis of symmetry of the square $A F D E$, we have $\angle A P E=\angle B P F$. Moreover, $\angle A E P=135^{\circ}=\angle B F P$. Hence triangles $A P E$ and $B P F$ are similar, and $\angle C A P=\angle A B C$, i.e. the line $A P$ is tangent to the circumcircle of $A B C$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
09e14b2b-a883-5c25-8ae3-30129ebcd1ca
| 240,322
|
Given a triangle $A B C$ with $\angle A=120^{\circ}$. The points $K$ and $L$ lie on the sides $A B$ and $A C$, respectively. Let $B K P$ and $C L Q$ be equilateral triangles constructed outside the triangle $A B C$. Prove that
$$
|P Q| \geqslant \frac{\sqrt{3}}{2} \cdot(|A B|+|A C|) .
$$
|
Since $\angle A B C+\angle A C B=60^{\circ}$, the lines $B P$ and $C Q$ are parallel. Let $X$ and $Y$ be the feet of perpendiculars from $A$ to $B P$ and $C Q$, respectively (see Figure 4). Then $|A X|=\frac{\sqrt{3}}{2}|A B|$ and $|A Y|=\frac{\sqrt{3}}{2}|A C|$. Since the points $X, A$ and $Y$ are collinear, we get
$$
|P Q| \geqslant|X Y|=\frac{\sqrt{3}}{2}(|A B|+|A C|)
$$
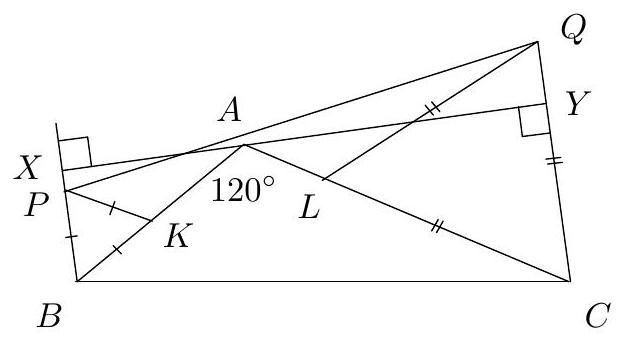
Figure 4
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a triangle $A B C$ with $\angle A=120^{\circ}$. The points $K$ and $L$ lie on the sides $A B$ and $A C$, respectively. Let $B K P$ and $C L Q$ be equilateral triangles constructed outside the triangle $A B C$. Prove that
$$
|P Q| \geqslant \frac{\sqrt{3}}{2} \cdot(|A B|+|A C|) .
$$
|
Since $\angle A B C+\angle A C B=60^{\circ}$, the lines $B P$ and $C Q$ are parallel. Let $X$ and $Y$ be the feet of perpendiculars from $A$ to $B P$ and $C Q$, respectively (see Figure 4). Then $|A X|=\frac{\sqrt{3}}{2}|A B|$ and $|A Y|=\frac{\sqrt{3}}{2}|A C|$. Since the points $X, A$ and $Y$ are collinear, we get
$$
|P Q| \geqslant|X Y|=\frac{\sqrt{3}}{2}(|A B|+|A C|)
$$

Figure 4
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
ea599d25-b072-5013-b7d4-8c50add62080
| 240,330
|
Let $A B C$ be a triangle such that $\frac{|B C|}{|A B|-|B C|}=\frac{|A B|+|B C|}{|A C|}$. Determine the ratio $\angle A: \angle C$.
|
Answer: $1: 2$.
Denote $|B C|=a,|A C|=b,|A B|=c$. The condition $\frac{a}{c-a}=\frac{c+a}{b}$ implies $c^{2}=a^{2}+a b$ and
$$
\frac{c}{a+b}=\frac{a}{c} .
$$
Let $D$ be a point on $A B$ such that $|B D|=\frac{a}{a+b} \cdot c$ (see Figure 5). Then
$$
\frac{|B D|}{|B C|}=\frac{c}{a+b}=\frac{a}{c}=\frac{|B C|}{|B A|}
$$
so triangles $B C D$ and $B A C$ are similar, implying $\angle B C D=\angle B A C$. Also, $\frac{|A C|}{|B C|}=\frac{|A D|}{|B D|}$ yields $\frac{|B C|}{|B D|}=\frac{|A C|}{|A D|}$, and hence by the bisector theorem $C D$ is the bisector of $\angle B C A$. So the ratio asked for is $1: 2$.
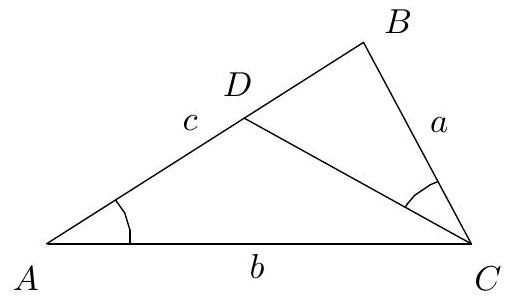
Figure 5
|
1: 2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle such that $\frac{|B C|}{|A B|-|B C|}=\frac{|A B|+|B C|}{|A C|}$. Determine the ratio $\angle A: \angle C$.
|
Answer: $1: 2$.
Denote $|B C|=a,|A C|=b,|A B|=c$. The condition $\frac{a}{c-a}=\frac{c+a}{b}$ implies $c^{2}=a^{2}+a b$ and
$$
\frac{c}{a+b}=\frac{a}{c} .
$$
Let $D$ be a point on $A B$ such that $|B D|=\frac{a}{a+b} \cdot c$ (see Figure 5). Then
$$
\frac{|B D|}{|B C|}=\frac{c}{a+b}=\frac{a}{c}=\frac{|B C|}{|B A|}
$$
so triangles $B C D$ and $B A C$ are similar, implying $\angle B C D=\angle B A C$. Also, $\frac{|A C|}{|B C|}=\frac{|A D|}{|B D|}$ yields $\frac{|B C|}{|B D|}=\frac{|A C|}{|A D|}$, and hence by the bisector theorem $C D$ is the bisector of $\angle B C A$. So the ratio asked for is $1: 2$.

Figure 5
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
1cc707c3-6f34-5c4b-ac71-6cc09a4eaead
| 240,339
|
Fredek runs a private hotel. He claims that whenever $n \geqslant 3$ guests visit the hotel, it is possible to select two guests who have equally many acquaintances among the other guests, and who also have a common acquaintance or a common unknown among the guests. For which values of $n$ is Fredek right?
(Acquaintance is a symmetric relation.)
|
Answer: Fredek is right for all $n \neq 4$.
Suppose that any two guests of Fredek having the same number of acquaintances have neither a common acquaintance nor a common unknown. From the set $\mathcal{K}$ of Fredek's guests choose any two guests $A$ and $B$ having the same number of acquaintances (the existence of such two guests follows from the pigeonhole principle). It then follows from our assumption that $A$ and $B$ have both either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$, depending on whether $A$ and $B$ are acquainted or not. This proves in particular that for any odd $n$ Fredek is right.
Assume now that $n$ is even, and $n \geqslant 6$. Choose from $\mathcal{K} \backslash\{A, B\}$ two
guests $C, D$ with the same number of acquaintances in $\mathcal{K} \backslash\{A, B\}$. Since every guest in $\mathcal{K} \backslash\{A, B\}$ is acquaintance either with $A$ or with $B$ but not with both, $C$ and $D$ have the same number of acquaintances in $\mathcal{K}$, which implies that they both have either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$.
Finally, choose from $\mathcal{K} \backslash\{A, B, C, D\}$ two guests $E, F$ with the same number of acquaintances in $\mathcal{K} \backslash\{A, B, C, D\}$ (this is possible as $n \geqslant 6$ ). Since every guest in $\mathcal{K} \backslash\{A, B, C, D\}$ has exactly two acquaintances in the set $\{A, B, C, D\}$, the guests $E$ and $F$ have the same number of acquaintances in $\mathcal{K}$, which means that they both have either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$. Thus at least four people among $A, B, C, D, E, F$ have the same number of acquaintances in $\mathcal{K}$. Select any three of these four guests - then one of these three is either a common acquaintance or a common unknown for the other two.
For $n=4$ Fredek is not right. The diagram on Figure 6 gives the counterexample (where points indicate guests and lines show acquaintances).
Figure 6
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Fredek runs a private hotel. He claims that whenever $n \geqslant 3$ guests visit the hotel, it is possible to select two guests who have equally many acquaintances among the other guests, and who also have a common acquaintance or a common unknown among the guests. For which values of $n$ is Fredek right?
(Acquaintance is a symmetric relation.)
|
Answer: Fredek is right for all $n \neq 4$.
Suppose that any two guests of Fredek having the same number of acquaintances have neither a common acquaintance nor a common unknown. From the set $\mathcal{K}$ of Fredek's guests choose any two guests $A$ and $B$ having the same number of acquaintances (the existence of such two guests follows from the pigeonhole principle). It then follows from our assumption that $A$ and $B$ have both either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$, depending on whether $A$ and $B$ are acquainted or not. This proves in particular that for any odd $n$ Fredek is right.
Assume now that $n$ is even, and $n \geqslant 6$. Choose from $\mathcal{K} \backslash\{A, B\}$ two
guests $C, D$ with the same number of acquaintances in $\mathcal{K} \backslash\{A, B\}$. Since every guest in $\mathcal{K} \backslash\{A, B\}$ is acquaintance either with $A$ or with $B$ but not with both, $C$ and $D$ have the same number of acquaintances in $\mathcal{K}$, which implies that they both have either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$.
Finally, choose from $\mathcal{K} \backslash\{A, B, C, D\}$ two guests $E, F$ with the same number of acquaintances in $\mathcal{K} \backslash\{A, B, C, D\}$ (this is possible as $n \geqslant 6$ ). Since every guest in $\mathcal{K} \backslash\{A, B, C, D\}$ has exactly two acquaintances in the set $\{A, B, C, D\}$, the guests $E$ and $F$ have the same number of acquaintances in $\mathcal{K}$, which means that they both have either $\frac{1}{2} n$ or $\frac{1}{2} n-1$ acquaintances in $\mathcal{K}$. Thus at least four people among $A, B, C, D, E, F$ have the same number of acquaintances in $\mathcal{K}$. Select any three of these four guests - then one of these three is either a common acquaintance or a common unknown for the other two.
For $n=4$ Fredek is not right. The diagram on Figure 6 gives the counterexample (where points indicate guests and lines show acquaintances).

Figure 6
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\n6."
}
|
2f1bade9-01a1-557f-b42d-4dda4558d442
| 240,348
|
In a $40 \times 50$ array of control buttons, each button has two states: $\mathrm{ON}$ and OFF. By touching a button, its state and the states of all buttons in the same row and in the same column are switched. Prove that the array of control buttons may be altered from the all-OFF state to the all-ON state by touching buttons successively, and determine the least number of touches needed to do so.
|
Answer: 2000 .
Altering the state from all-OFF to all-ON requires that the state of each button is changed an odd number of times. This is achieved by touching each button once. We prove that the desired result cannot be achieved if some button is never touched. In order to turn this button ON, the total number of touches of the other buttons in its row and column must be odd. Hence either the other buttons in its row or in its column - say, in its row - must be touched an odd number of times altogether. In order to change the state of each of these (odd number of) buttons an odd number of times, the total number of touches of all the other buttons on the panel (i.e. outside of the selected row) must be even. But then we have an even
total number of state changes for the (odd number of) other buttons in the selected column, whereas an odd number is required to alter the state of all these buttons. Hence the minimal number of touches is $40 \cdot 50=2000$.
|
2000
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a $40 \times 50$ array of control buttons, each button has two states: $\mathrm{ON}$ and OFF. By touching a button, its state and the states of all buttons in the same row and in the same column are switched. Prove that the array of control buttons may be altered from the all-OFF state to the all-ON state by touching buttons successively, and determine the least number of touches needed to do so.
|
Answer: 2000 .
Altering the state from all-OFF to all-ON requires that the state of each button is changed an odd number of times. This is achieved by touching each button once. We prove that the desired result cannot be achieved if some button is never touched. In order to turn this button ON, the total number of touches of the other buttons in its row and column must be odd. Hence either the other buttons in its row or in its column - say, in its row - must be touched an odd number of times altogether. In order to change the state of each of these (odd number of) buttons an odd number of times, the total number of touches of all the other buttons on the panel (i.e. outside of the selected row) must be even. But then we have an even
total number of state changes for the (odd number of) other buttons in the selected column, whereas an odd number is required to alter the state of all these buttons. Hence the minimal number of touches is $40 \cdot 50=2000$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\n7."
}
|
eba77462-3b0b-58ff-b9c6-2330e6acd01a
| 240,356
|
Fourteen friends met at a party. One of them, Fredek, wanted to go to bed early. He said goodbye to 10 of his friends, forgot about the remaining 3 , and went to bed. After a while he returned to the party, said goodbye to 10 of his friends (not necessarily the same as before), and went to bed. Later Fredek came back a number of times, each time saying goodbye to exactly 10 of his friends, and then went back to bed. As soon as he had said goodbye to each of his friends at least once, he did not come back again. In the morning Fredek realised that he had said goodbye a different number of times to each of his thirteen friends! What is the smallest possible number of times that Fredek returned to the party?
|
Answer: Fredek returned at least 32 times.
Assume Fredek returned $k$ times, i.e. he was saying good-bye $k+1$ times to his friends. There exists a friend of Fredek, call him $X_{13}$, about whom Fredek forgot $k$ times in a row, starting from the very first time - otherwise Fredek would have come back less than $k$ times.
Consider the remaining friends of Fredek: $X_{1}, X_{2}, \ldots, X_{12}$. Assume that Fredek forgot $x_{j}$ times about each friend $X_{j}$. Since Fredek forgot a different number of times about each of his friends, so we can assume w.l.o.g. that $x_{j} \geqslant j-1$ for $j=1,2, \ldots, 12$. Since $X_{13}$ was forgotten by Fredek $k$ times, and since Fredek forgot about exactly three of his friends each time, we have
$$
\begin{aligned}
3(k+1) & =x_{1}+x_{2}+x_{3}+\ldots+x_{12}+k \geqslant \\
& \geqslant 0+1+2+3+\ldots+11+k= \\
& =66+k .
\end{aligned}
$$
Therefore $2 k \geqslant 63$, which gives $k \geqslant 32$.
It is possible that Fredek returned 32 times, i.e. he was saying good-bye 33 times to his friends. The following table shows this. The $i$-th column displays the three friends Fredek forgot while saying good-bye for the $i$-th time (i.e. before his $i$-th return). For simplicity we write $j$ in place of $X_{j}$.
$$
\begin{aligned}
& 13 \ldots .131313 \ldots .1313 \ldots .131313131313131311
\end{aligned}
$$
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Fourteen friends met at a party. One of them, Fredek, wanted to go to bed early. He said goodbye to 10 of his friends, forgot about the remaining 3 , and went to bed. After a while he returned to the party, said goodbye to 10 of his friends (not necessarily the same as before), and went to bed. Later Fredek came back a number of times, each time saying goodbye to exactly 10 of his friends, and then went back to bed. As soon as he had said goodbye to each of his friends at least once, he did not come back again. In the morning Fredek realised that he had said goodbye a different number of times to each of his thirteen friends! What is the smallest possible number of times that Fredek returned to the party?
|
Answer: Fredek returned at least 32 times.
Assume Fredek returned $k$ times, i.e. he was saying good-bye $k+1$ times to his friends. There exists a friend of Fredek, call him $X_{13}$, about whom Fredek forgot $k$ times in a row, starting from the very first time - otherwise Fredek would have come back less than $k$ times.
Consider the remaining friends of Fredek: $X_{1}, X_{2}, \ldots, X_{12}$. Assume that Fredek forgot $x_{j}$ times about each friend $X_{j}$. Since Fredek forgot a different number of times about each of his friends, so we can assume w.l.o.g. that $x_{j} \geqslant j-1$ for $j=1,2, \ldots, 12$. Since $X_{13}$ was forgotten by Fredek $k$ times, and since Fredek forgot about exactly three of his friends each time, we have
$$
\begin{aligned}
3(k+1) & =x_{1}+x_{2}+x_{3}+\ldots+x_{12}+k \geqslant \\
& \geqslant 0+1+2+3+\ldots+11+k= \\
& =66+k .
\end{aligned}
$$
Therefore $2 k \geqslant 63$, which gives $k \geqslant 32$.
It is possible that Fredek returned 32 times, i.e. he was saying good-bye 33 times to his friends. The following table shows this. The $i$-th column displays the three friends Fredek forgot while saying good-bye for the $i$-th time (i.e. before his $i$-th return). For simplicity we write $j$ in place of $X_{j}$.
$$
\begin{aligned}
& 13 \ldots .131313 \ldots .1313 \ldots .131313131313131311
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
aa416b98-3d44-59d0-8520-368cd65ee518
| 604,506
|
There is a frog jumping on a $2 k \times 2 k$ chessboard, composed of unit squares. The frog's jumps are of length $\sqrt{1+k^{2}}$ and they carry the frog from the center of a square to the center of another square. Some $m$ squares of the board are marked with an $x$, and all the squares into which the frog can jump from an $x$ 'd square (whether they carry an $x$ or not) are marked with an $\circ$. There are $n \circ$ 'd squares. Prove that $n \geqslant m$.
|
Label the squares by pairs of integers $(i, j)$ where $1 \leqslant i, j \leqslant 2 k$. Let $L$ be the set of all such pairs. Define a function $f: L \rightarrow L$ by
$$
f(i, j)= \begin{cases}(i+1, j+k) & \text { for } i \text { odd and } j \leqslant k \\ (i-1, j+k) & \text { for } i \text { even and } j \leqslant k, \\ (i+1, j-k) & \text { for } i \text { odd and } j>k, \\ (i-1, j-k) & \text { for } i \text { even and } j>k\end{cases}
$$
It is easy to see that $f$ is one-to-one. Let $X \subset L$ be the set of $\times^{\prime} \mathrm{d}$ squares and $O \subset L$ the set of o'd squares. Since the distance from $(i, j)$ to
$(i \pm 1, j \pm k)$ is $\sqrt{1+k^{2}}$, we have $f(i, j) \in O$ for every $(i, j) \in X$. Now, since $f$ is one-to-one, the number of elements in $f(S)$ is the same as the number of elements in $S$. As $f(X) \subset O$, the number of elements in $X$ is at most the number of elements in $O$, or $m \leqslant n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a frog jumping on a $2 k \times 2 k$ chessboard, composed of unit squares. The frog's jumps are of length $\sqrt{1+k^{2}}$ and they carry the frog from the center of a square to the center of another square. Some $m$ squares of the board are marked with an $x$, and all the squares into which the frog can jump from an $x$ 'd square (whether they carry an $x$ or not) are marked with an $\circ$. There are $n \circ$ 'd squares. Prove that $n \geqslant m$.
|
Label the squares by pairs of integers $(i, j)$ where $1 \leqslant i, j \leqslant 2 k$. Let $L$ be the set of all such pairs. Define a function $f: L \rightarrow L$ by
$$
f(i, j)= \begin{cases}(i+1, j+k) & \text { for } i \text { odd and } j \leqslant k \\ (i-1, j+k) & \text { for } i \text { even and } j \leqslant k, \\ (i+1, j-k) & \text { for } i \text { odd and } j>k, \\ (i-1, j-k) & \text { for } i \text { even and } j>k\end{cases}
$$
It is easy to see that $f$ is one-to-one. Let $X \subset L$ be the set of $\times^{\prime} \mathrm{d}$ squares and $O \subset L$ the set of o'd squares. Since the distance from $(i, j)$ to
$(i \pm 1, j \pm k)$ is $\sqrt{1+k^{2}}$, we have $f(i, j) \in O$ for every $(i, j) \in X$. Now, since $f$ is one-to-one, the number of elements in $f(S)$ is the same as the number of elements in $S$. As $f(X) \subset O$, the number of elements in $X$ is at most the number of elements in $O$, or $m \leqslant n$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\n9."
}
|
4955608d-da38-58ae-a230-b695c9124612
| 240,374
|
Two positive integers are written on the blackboard. Initially, one of them is 2000 and the other is smaller than 2000. If the arithmetic mean $m$ of the two numbers on the blackboard is an integer, the following operation is allowed: one of the two numbers is erased and replaced by $m$. Prove that this operation cannot be performed more than ten times. Give an example where the operation can be performed ten times.
|
Each time the operation is performed, the difference between the two numbers on the blackboard will become one half of its previous value (regardless of which number was erased). The mean value of two integers is an integer if and only if their difference is an even number. Suppose the initial numbers were $a=2000$ and $b$. It follows that the operation can be performed $n$ times if and only if $a-b$ is of the form $2^{n} u$. This shows that $n \leqslant 10$ since $2^{11}>2000$. Choosing $b=976$ so that $a-b=1024=2^{10}$, the operation can be performed 10 times.
|
10
|
Yes
|
Yes
|
proof
|
Number Theory
|
Two positive integers are written on the blackboard. Initially, one of them is 2000 and the other is smaller than 2000. If the arithmetic mean $m$ of the two numbers on the blackboard is an integer, the following operation is allowed: one of the two numbers is erased and replaced by $m$. Prove that this operation cannot be performed more than ten times. Give an example where the operation can be performed ten times.
|
Each time the operation is performed, the difference between the two numbers on the blackboard will become one half of its previous value (regardless of which number was erased). The mean value of two integers is an integer if and only if their difference is an even number. Suppose the initial numbers were $a=2000$ and $b$. It follows that the operation can be performed $n$ times if and only if $a-b$ is of the form $2^{n} u$. This shows that $n \leqslant 10$ since $2^{11}>2000$. Choosing $b=976$ so that $a-b=1024=2^{10}$, the operation can be performed 10 times.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\n10."
}
|
eb2a6a9f-817b-5e31-9b19-0029efcef53b
| 604,540
|
A sequence of positive integers $a_{1}, a_{2}, \ldots$ is such that for each $m$ and $n$ the following holds: if $m$ is a divisor of $n$ and $m<n$, then $a_{m}$ is a divisor of $a_{n}$ and $a_{m}<a_{n}$. Find the least possible value of $a_{2000}$.
|
Answer: 128.
Let $d$ denote the least possible value of $a_{2000}$. We shall prove that $d=128$.
Clearly the sequence defined by $a_{1}=1$ and $a_{n}=2^{\alpha_{1}+\alpha_{2}+\cdots+\alpha_{k}}$ for $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots \cdots p_{k}^{\alpha_{k}}$ has the required property. Since $2000=2^{4} \cdot 5^{3}$, we have $a_{2000}=2^{4+3}=128$ and therefore $d \leqslant 128$.
Note that in the sequence $1<5<25<125<250<500<1000<2000$ each term is divisible by the previous one. As $a_{1} \geqslant 1$ it follows that
$$
a_{2000} \geqslant 2 \cdot a_{1000} \geqslant 2^{2} \cdot a_{500} \geqslant 2^{3} \cdot a_{250} \geqslant \ldots \geqslant 2^{7} \cdot a_{1} \geqslant 2^{7}=128 .
$$
|
128
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence of positive integers $a_{1}, a_{2}, \ldots$ is such that for each $m$ and $n$ the following holds: if $m$ is a divisor of $n$ and $m<n$, then $a_{m}$ is a divisor of $a_{n}$ and $a_{m}<a_{n}$. Find the least possible value of $a_{2000}$.
|
Answer: 128.
Let $d$ denote the least possible value of $a_{2000}$. We shall prove that $d=128$.
Clearly the sequence defined by $a_{1}=1$ and $a_{n}=2^{\alpha_{1}+\alpha_{2}+\cdots+\alpha_{k}}$ for $n=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots \cdots p_{k}^{\alpha_{k}}$ has the required property. Since $2000=2^{4} \cdot 5^{3}$, we have $a_{2000}=2^{4+3}=128$ and therefore $d \leqslant 128$.
Note that in the sequence $1<5<25<125<250<500<1000<2000$ each term is divisible by the previous one. As $a_{1} \geqslant 1$ it follows that
$$
a_{2000} \geqslant 2 \cdot a_{1000} \geqslant 2^{2} \cdot a_{500} \geqslant 2^{3} \cdot a_{250} \geqslant \ldots \geqslant 2^{7} \cdot a_{1} \geqslant 2^{7}=128 .
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
9c42bd35-eb49-50cd-93ab-ec11d9558097
| 240,391
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive integers such that no one of them is an initial fragment of any other (for example, 12 is an initial fragment of $\underline{12}, \underline{12} 5$ and
12405). Prove that
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<3
$$
|
Let $\left\{y_{1}, \ldots, y_{k}\right\} \subset\left\{x_{1}, \ldots, x_{n}\right\}$ be a subset of numbers with the maximal number of digits, and differing from one another only by their last digits: $y_{1}=\overline{y \alpha_{1}}, y_{2}=\overline{y \alpha_{2}}, \ldots, y_{k}=\overline{y \alpha_{k}}$ (here $\overline{y \alpha_{i}}$ denotes the number consisting of $y$ as its initial fragment and $\alpha_{i}$ as its last digit). Then we have
$$
\frac{1}{y_{1}}+\ldots+\frac{1}{y_{k}} \leqslant \frac{1}{\overline{y 0}}+\ldots+\frac{1}{\overline{y 9}}<10 \cdot \frac{1}{\overline{y 0}}=\frac{1}{y}
$$
Let's replace all numbers $y_{1}, y_{2}, \ldots, y_{k}$ by a single $y$ in the set $\left\{x_{1}, \ldots, x_{n}\right\}$. Then the obtained set of numbers still has the property mentioned in the statement of the problem, and the sum of their reciprocals does not decrease. Continuing to reduce the given set of numbers in the same way, we finally obtain
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}} \leqslant \frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{9}<3
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be positive integers such that no one of them is an initial fragment of any other (for example, 12 is an initial fragment of $\underline{12}, \underline{12} 5$ and
12405). Prove that
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}}<3
$$
|
Let $\left\{y_{1}, \ldots, y_{k}\right\} \subset\left\{x_{1}, \ldots, x_{n}\right\}$ be a subset of numbers with the maximal number of digits, and differing from one another only by their last digits: $y_{1}=\overline{y \alpha_{1}}, y_{2}=\overline{y \alpha_{2}}, \ldots, y_{k}=\overline{y \alpha_{k}}$ (here $\overline{y \alpha_{i}}$ denotes the number consisting of $y$ as its initial fragment and $\alpha_{i}$ as its last digit). Then we have
$$
\frac{1}{y_{1}}+\ldots+\frac{1}{y_{k}} \leqslant \frac{1}{\overline{y 0}}+\ldots+\frac{1}{\overline{y 9}}<10 \cdot \frac{1}{\overline{y 0}}=\frac{1}{y}
$$
Let's replace all numbers $y_{1}, y_{2}, \ldots, y_{k}$ by a single $y$ in the set $\left\{x_{1}, \ldots, x_{n}\right\}$. Then the obtained set of numbers still has the property mentioned in the statement of the problem, and the sum of their reciprocals does not decrease. Continuing to reduce the given set of numbers in the same way, we finally obtain
$$
\frac{1}{x_{1}}+\frac{1}{x_{2}}+\cdots+\frac{1}{x_{n}} \leqslant \frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{9}<3
$$
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
94656215-49a9-5c5e-aa32-1fb80ab992f9
| 240,401
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be an arithmetic progression of integers such that $i$ divides $a_{i}$ for $i=1,2, \ldots, n-1$ and $n$ does not divide $a_{n}$. Prove that $n$ is a power of a prime.
|
Assume $a_{i}=k+d i$ for $i=1,2, \ldots, n$. Then $k$ is a multiple of every $i \in\{1,2, \ldots, n-1\}$ but not a multiple of $n$. If $n=a b$ with $a, b>1$ and $\operatorname{gcd}(a, b)=1$, then $k$ is divisible by both $a$ and $b$, but not by $n$, which is a contradiction. Hence, $n$ has only one prime factor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be an arithmetic progression of integers such that $i$ divides $a_{i}$ for $i=1,2, \ldots, n-1$ and $n$ does not divide $a_{n}$. Prove that $n$ is a power of a prime.
|
Assume $a_{i}=k+d i$ for $i=1,2, \ldots, n$. Then $k$ is a multiple of every $i \in\{1,2, \ldots, n-1\}$ but not a multiple of $n$. If $n=a b$ with $a, b>1$ and $\operatorname{gcd}(a, b)=1$, then $k$ is divisible by both $a$ and $b$, but not by $n$, which is a contradiction. Hence, $n$ has only one prime factor.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
fa0807f8-6260-5b0d-9597-6f0dd217d888
| 240,410
|
Find all positive integers $n$ such that $n$ is equal to 100 times the number of positive divisors of $n$.
|
Answer: 2000 is the only such integer.
Let $d(n)$ denote the number of positive divisors of $n$ and $p \triangleright n$ denote the exponent of the prime $p$ in the canonical representation of $n$. Let $\delta(n)=\frac{n}{d(n)}$. Using this notation, the problem reformulates as follows: Find all positive integers $n$ such that $\delta(n)=100$.
Lemma: Let $n$ be an integer and $m$ its proper divisor. Then $\delta(m) \leqslant \delta(n)$ and the equality holds if and only if $m$ is odd and $n=2 m$.
Proof. Let $n=m p$ for a prime $p$. By the well-known formula
$$
d(n)=\prod_{p}(1+p \triangleright n)
$$
we have
$$
\frac{\delta(n)}{\delta(m)}=\frac{n}{m} \cdot \frac{d(m)}{d(n)}=p \cdot \frac{1+p \triangleright m}{1+p \triangleright n}=p \cdot \frac{p \triangleright n}{1+p \triangleright n} \geqslant 2 \cdot \frac{1}{2}=1,
$$
hence $\delta(m) \leqslant \delta(n)$. It is also clear that equality holds if and only if $p=2$ and $p \triangleright n=1$, i.e. $m$ is odd and $n=2 m$.
For the general case $n=m s$ where $s>1$ is an arbitrary positive integer, represent $s$ as a product of primes. By elementary induction on the number of factors in the representation we prove $\delta(m) \leqslant \delta(n)$. The equality can hold only if all factors are equal to 2 and the number $m$ as well as any intermediate result of multiplying it by these factors is odd, i.e. the representation of $s$ consists of a single prime 2, which gives $n=2 m$. This proves the lemma.
Now assume that $\delta(n)=100$ for some $n$, i.e. $n=100 \cdot d(n)=2^{2} \cdot 5^{2} \cdot d(n)$. In the following, we estimate the exponents of primes in the canonical representation of $n$, using the fact that 100 is a divisor of $n$.
(1) Observe that $\delta\left(2^{7} \cdot 5^{2}\right)=\frac{2^{5} \cdot 100}{8 \cdot 3}=\frac{3200}{24}>100$. Hence $2 \triangleright n \leqslant 6$, since otherwise $2^{7} \cdot 5^{2}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(2) Observe that $\delta\left(2^{2} \cdot 5^{4}\right)=\frac{5^{2} \cdot 100}{3 \cdot 5}=\frac{2500}{15}>100$. Hence $5 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(3) Observe that $\delta\left(2^{2} \cdot 5^{2} \cdot 3^{4}\right)=\frac{3^{4} \cdot 100}{3 \cdot 3 \cdot 5}=\frac{8100}{45}>100$. Hence $3 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{2} \cdot 3^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(4) Take a prime $q>5$ and an integer $k \geqslant 4$. Then
$$
\begin{aligned}
\delta\left(2^{2} \cdot 5^{2} \cdot q^{k}\right) & =\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot q^{k}\right)}=\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}>\frac{2^{2} \cdot 5^{2} \cdot 3^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}= \\
& =\delta\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)>100 .
\end{aligned}
$$
Hence, similarly to the previous cases, we get $q \triangleright n \leqslant 3$.
(5) If a prime $q>7$ divides $n$, then $q$ divides $d(n)$. Thus $q$ divides $1+p \triangleright n$ for some prime $p$. But this is impossible because, as the previous cases showed, $p \triangleright n \leqslant 6$ for all $p$. So $n$ is not divisible by primes greater than 7 .
(6) If 7 divides $n$, then 7 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=6$. At the same time, if $2 \triangleright n=6$, then 7 divides $d(n)$ and $n$. So 7 divides $n$ if and only if $2 \triangleright n=6$. Since $\delta\left(2^{6} \cdot 5^{2} \cdot 7\right)=\frac{2^{4} \cdot 7 \cdot 100}{7 \cdot 3 \cdot 2}=\frac{11200}{42}>100$, both of these conditions cannot hold simultaneously. So $n$ is not divisible by 7 and $2 \triangleright n \leqslant 5$.
(7) If $5 \triangleright n=3$, then 5 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=4$. At the same time, if $2 \triangleright n=4$, then 5 divides $d(n), 5^{3}$ divides $n$ and, by (2), $5 \triangleright n=3$. So $5 \triangleright n=3$ if and only if $2 \triangleright n=4$. Since $\delta\left(2^{4} \cdot 5^{3}\right)=\frac{2^{2} \cdot 5 \cdot 100}{5 \cdot 4}=100$, we find that $n=2^{4} \cdot 5^{3}=2000$ satisfies the required condition. On the other hand, if $2 \triangleright n=4$ and $5 \triangleright n=3$ for some $n \neq 2000$, then $n=2000 s$ for some $s>1$ and, by the lemma, $\delta(n)>100$.
(8) The case $5 \triangleright n=2$ has remained. By (7), we have $2 \triangleright n \neq 4$, so $2 \triangleright n \in\{2,3,5\}$. The condition $5 \triangleright n=2$ implies that 3 divides $d(n)$ and $n$, thus $3 \triangleright n \in\{1,2,3\}$. If $2 \triangleright n=3$, then $d(n)$ is divisible by 2 but not by 4 . At the same time $2 \triangleright n=3$ implies $3+1=4$ divides $d(n)$, a contradiction. Thus $2 \triangleright n \in\{2,5\}$, and $3^{2}$ divides $d(n)$ and $n$, i.e.
$3 \triangleright n \in\{2,3\}$. Now $3 \triangleright n=2$ would imply that $3^{3}$ divides $d(n)$ and $n$, a contradiction; on the other hand $3 \triangleright n=3$ would imply $3 \triangleright d(n)=2$ and hence $3 \triangleright n=2$, a contradiction.
|
2000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that $n$ is equal to 100 times the number of positive divisors of $n$.
|
Answer: 2000 is the only such integer.
Let $d(n)$ denote the number of positive divisors of $n$ and $p \triangleright n$ denote the exponent of the prime $p$ in the canonical representation of $n$. Let $\delta(n)=\frac{n}{d(n)}$. Using this notation, the problem reformulates as follows: Find all positive integers $n$ such that $\delta(n)=100$.
Lemma: Let $n$ be an integer and $m$ its proper divisor. Then $\delta(m) \leqslant \delta(n)$ and the equality holds if and only if $m$ is odd and $n=2 m$.
Proof. Let $n=m p$ for a prime $p$. By the well-known formula
$$
d(n)=\prod_{p}(1+p \triangleright n)
$$
we have
$$
\frac{\delta(n)}{\delta(m)}=\frac{n}{m} \cdot \frac{d(m)}{d(n)}=p \cdot \frac{1+p \triangleright m}{1+p \triangleright n}=p \cdot \frac{p \triangleright n}{1+p \triangleright n} \geqslant 2 \cdot \frac{1}{2}=1,
$$
hence $\delta(m) \leqslant \delta(n)$. It is also clear that equality holds if and only if $p=2$ and $p \triangleright n=1$, i.e. $m$ is odd and $n=2 m$.
For the general case $n=m s$ where $s>1$ is an arbitrary positive integer, represent $s$ as a product of primes. By elementary induction on the number of factors in the representation we prove $\delta(m) \leqslant \delta(n)$. The equality can hold only if all factors are equal to 2 and the number $m$ as well as any intermediate result of multiplying it by these factors is odd, i.e. the representation of $s$ consists of a single prime 2, which gives $n=2 m$. This proves the lemma.
Now assume that $\delta(n)=100$ for some $n$, i.e. $n=100 \cdot d(n)=2^{2} \cdot 5^{2} \cdot d(n)$. In the following, we estimate the exponents of primes in the canonical representation of $n$, using the fact that 100 is a divisor of $n$.
(1) Observe that $\delta\left(2^{7} \cdot 5^{2}\right)=\frac{2^{5} \cdot 100}{8 \cdot 3}=\frac{3200}{24}>100$. Hence $2 \triangleright n \leqslant 6$, since otherwise $2^{7} \cdot 5^{2}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(2) Observe that $\delta\left(2^{2} \cdot 5^{4}\right)=\frac{5^{2} \cdot 100}{3 \cdot 5}=\frac{2500}{15}>100$. Hence $5 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(3) Observe that $\delta\left(2^{2} \cdot 5^{2} \cdot 3^{4}\right)=\frac{3^{4} \cdot 100}{3 \cdot 3 \cdot 5}=\frac{8100}{45}>100$. Hence $3 \triangleright n \leqslant 3$, since otherwise $2^{2} \cdot 5^{2} \cdot 3^{4}$ divides $n$ and, by the lemma, $\delta(n)>100$.
(4) Take a prime $q>5$ and an integer $k \geqslant 4$. Then
$$
\begin{aligned}
\delta\left(2^{2} \cdot 5^{2} \cdot q^{k}\right) & =\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot q^{k}\right)}=\frac{2^{2} \cdot 5^{2} \cdot q^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}>\frac{2^{2} \cdot 5^{2} \cdot 3^{k}}{d\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)}= \\
& =\delta\left(2^{2} \cdot 5^{2} \cdot 3^{k}\right)>100 .
\end{aligned}
$$
Hence, similarly to the previous cases, we get $q \triangleright n \leqslant 3$.
(5) If a prime $q>7$ divides $n$, then $q$ divides $d(n)$. Thus $q$ divides $1+p \triangleright n$ for some prime $p$. But this is impossible because, as the previous cases showed, $p \triangleright n \leqslant 6$ for all $p$. So $n$ is not divisible by primes greater than 7 .
(6) If 7 divides $n$, then 7 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=6$. At the same time, if $2 \triangleright n=6$, then 7 divides $d(n)$ and $n$. So 7 divides $n$ if and only if $2 \triangleright n=6$. Since $\delta\left(2^{6} \cdot 5^{2} \cdot 7\right)=\frac{2^{4} \cdot 7 \cdot 100}{7 \cdot 3 \cdot 2}=\frac{11200}{42}>100$, both of these conditions cannot hold simultaneously. So $n$ is not divisible by 7 and $2 \triangleright n \leqslant 5$.
(7) If $5 \triangleright n=3$, then 5 divides $d(n)$ and hence divides $1+p \triangleright n$ for some prime $p$. By (1)-(4), this implies $p=2$ and $2 \triangleright n=4$. At the same time, if $2 \triangleright n=4$, then 5 divides $d(n), 5^{3}$ divides $n$ and, by (2), $5 \triangleright n=3$. So $5 \triangleright n=3$ if and only if $2 \triangleright n=4$. Since $\delta\left(2^{4} \cdot 5^{3}\right)=\frac{2^{2} \cdot 5 \cdot 100}{5 \cdot 4}=100$, we find that $n=2^{4} \cdot 5^{3}=2000$ satisfies the required condition. On the other hand, if $2 \triangleright n=4$ and $5 \triangleright n=3$ for some $n \neq 2000$, then $n=2000 s$ for some $s>1$ and, by the lemma, $\delta(n)>100$.
(8) The case $5 \triangleright n=2$ has remained. By (7), we have $2 \triangleright n \neq 4$, so $2 \triangleright n \in\{2,3,5\}$. The condition $5 \triangleright n=2$ implies that 3 divides $d(n)$ and $n$, thus $3 \triangleright n \in\{1,2,3\}$. If $2 \triangleright n=3$, then $d(n)$ is divisible by 2 but not by 4 . At the same time $2 \triangleright n=3$ implies $3+1=4$ divides $d(n)$, a contradiction. Thus $2 \triangleright n \in\{2,5\}$, and $3^{2}$ divides $d(n)$ and $n$, i.e.
$3 \triangleright n \in\{2,3\}$. Now $3 \triangleright n=2$ would imply that $3^{3}$ divides $d(n)$ and $n$, a contradiction; on the other hand $3 \triangleright n=3$ would imply $3 \triangleright d(n)=2$ and hence $3 \triangleright n=2$, a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
82bb9477-1cd7-5a98-a5aa-5f31c355e0f0
| 240,419
|
Let $n$ be a positive integer not divisible by 2 or 3 . Prove that for all integers $k$, the number $(k+1)^{n}-k^{n}-1$ is divisible by $k^{2}+k+1$.
|
Note that $n$ must be congruent to 1 or 5 modulo 6 , and proceed by induction on $\lfloor n / 6\rfloor$. It can easily be checked that the assertion holds for $n \in\{1,5\}$. Let $n>6$, and put $t=k^{2}+k+1$. The claim follows by:
$$
\begin{aligned}
(k+1)^{n}-k^{n}-1 & =(t+k)(k+1)^{n-2}-(t-(k+1)) k^{n-2}-1 \\
& \equiv k(k+1)^{n-2}+(k+1) k^{n-2}-1 \\
& \equiv(t-1)\left((k+1)^{n-3}+k^{n-3}\right)-1 \\
& \equiv-(k+1)^{n-3}-k^{n-3}-1 \\
& \equiv-(t+k)(k+1)^{n-5}-(t-(k+1)) k^{n-5}-1 \\
& \equiv-k(k+1)^{n-5}+(k+1) k^{n-5}-1 \\
& \equiv-(t-1)\left((k+1)^{n-6}-k^{n-6}\right)-1 \\
& \equiv(k+1)^{n-6}-k^{n-6}-1(\bmod t) .
\end{aligned}
$$
Alternative solution. Let $P(k)=(k+1)^{n}-k^{n}-1$, and let $\omega_{1}, \omega_{2}$ be the two roots of the quadratic polynomial $k^{2}+k+1$. The problem is then equivalent to showing that $P\left(\omega_{1}\right)=P\left(\omega_{2}\right)=0$ when $\operatorname{gcd}(n, 6)=1$, which is easy to check.
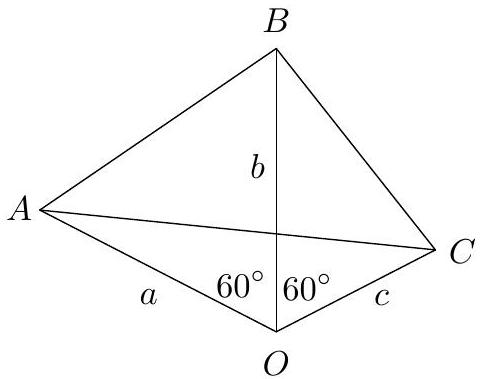
Figure 7
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer not divisible by 2 or 3 . Prove that for all integers $k$, the number $(k+1)^{n}-k^{n}-1$ is divisible by $k^{2}+k+1$.
|
Note that $n$ must be congruent to 1 or 5 modulo 6 , and proceed by induction on $\lfloor n / 6\rfloor$. It can easily be checked that the assertion holds for $n \in\{1,5\}$. Let $n>6$, and put $t=k^{2}+k+1$. The claim follows by:
$$
\begin{aligned}
(k+1)^{n}-k^{n}-1 & =(t+k)(k+1)^{n-2}-(t-(k+1)) k^{n-2}-1 \\
& \equiv k(k+1)^{n-2}+(k+1) k^{n-2}-1 \\
& \equiv(t-1)\left((k+1)^{n-3}+k^{n-3}\right)-1 \\
& \equiv-(k+1)^{n-3}-k^{n-3}-1 \\
& \equiv-(t+k)(k+1)^{n-5}-(t-(k+1)) k^{n-5}-1 \\
& \equiv-k(k+1)^{n-5}+(k+1) k^{n-5}-1 \\
& \equiv-(t-1)\left((k+1)^{n-6}-k^{n-6}\right)-1 \\
& \equiv(k+1)^{n-6}-k^{n-6}-1(\bmod t) .
\end{aligned}
$$
Alternative solution. Let $P(k)=(k+1)^{n}-k^{n}-1$, and let $\omega_{1}, \omega_{2}$ be the two roots of the quadratic polynomial $k^{2}+k+1$. The problem is then equivalent to showing that $P\left(\omega_{1}\right)=P\left(\omega_{2}\right)=0$ when $\operatorname{gcd}(n, 6)=1$, which is easy to check.

Figure 7
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
85e6ceaf-059a-56dc-97ed-b4bc827e0f2b
| 604,640
|
Prove that for all positive real numbers $a, b, c$ we have
$$
\sqrt{a^{2}-a b+b^{2}}+\sqrt{b^{2}-b c+c^{2}} \geqslant \sqrt{a^{2}+a c+c^{2}} .
$$
|
If $|O A|=a,|O B|=b,|O C|=c$ (see Figure 7), then the inequality follows from $|A C| \leqslant|A B|+|B C|$ by applying the cosine theorem to triangles $A O B$,
$B O C$ and $A O C$. The same argument holds if the quadrangle $O A B C$ is concave.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b, c$ we have
$$
\sqrt{a^{2}-a b+b^{2}}+\sqrt{b^{2}-b c+c^{2}} \geqslant \sqrt{a^{2}+a c+c^{2}} .
$$
|
If $|O A|=a,|O B|=b,|O C|=c$ (see Figure 7), then the inequality follows from $|A C| \leqslant|A B|+|B C|$ by applying the cosine theorem to triangles $A O B$,
$B O C$ and $A O C$. The same argument holds if the quadrangle $O A B C$ is concave.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\n16."
}
|
ad4f64c3-a692-5ffb-a3c4-1ddfedd843d1
| 604,655
|
Find all real solutions to the following system of equations:
$$
\left\{\begin{aligned}
x+y+z+t & =5 \\
x y+y z+z t+t x & =4 \\
x y z+y z t+z t x+t x y & =3 \\
x y z t & =-1
\end{aligned}\right.
$$
|
Answer: $x=\frac{1 \pm \sqrt{2}}{2}, y=2, z=\frac{1 \mp \sqrt{2}}{2}, t=2$ or $x=2, y=\frac{1 \pm \sqrt{2}}{2}$, $z=2, t=\frac{1 \mp \sqrt{2}}{2}$.
Let $A=x+z$ and $B=y+t$. Then the system of equations is equivalent to
$$
\left\{\begin{aligned}
A+B & =5 \\
A B & =4 \\
B x z+A y t & =3 \\
(B x z) \cdot(A y t) & =-4 .
\end{aligned}\right.
$$
The first two of these equations imply $\{A, B\}=\{1,4\}$ and the last two give $\{B x z, A y t\}=\{-1,4\}$. Once $A=x+z, B=y+t, B x z$ and Ayt are known, it is easy to find the corresponding values of $x, y, z$ and $t$. The solutions are shown in the following table.
| $A$ | $B$ | Bxz | Ayt | $x, z$ | $y, t$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 4 | -1 | 4 | $\frac{1 \pm \sqrt{2}}{2}$ | 2 |
| 1 | 4 | 4 | -1 | - | - |
| 4 | 1 | -1 | 4 | - | - |
| 4 | 1 | 4 | -1 | 2 | $\frac{1 \pm \sqrt{2}}{2}$ |
|
x=\frac{1 \pm \sqrt{2}}{2}, y=2, z=\frac{1 \mp \sqrt{2}}{2}, t=2 \text{ or } x=2, y=\frac{1 \pm \sqrt{2}}{2}, z=2, t=\frac{1 \mp \sqrt{2}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real solutions to the following system of equations:
$$
\left\{\begin{aligned}
x+y+z+t & =5 \\
x y+y z+z t+t x & =4 \\
x y z+y z t+z t x+t x y & =3 \\
x y z t & =-1
\end{aligned}\right.
$$
|
Answer: $x=\frac{1 \pm \sqrt{2}}{2}, y=2, z=\frac{1 \mp \sqrt{2}}{2}, t=2$ or $x=2, y=\frac{1 \pm \sqrt{2}}{2}$, $z=2, t=\frac{1 \mp \sqrt{2}}{2}$.
Let $A=x+z$ and $B=y+t$. Then the system of equations is equivalent to
$$
\left\{\begin{aligned}
A+B & =5 \\
A B & =4 \\
B x z+A y t & =3 \\
(B x z) \cdot(A y t) & =-4 .
\end{aligned}\right.
$$
The first two of these equations imply $\{A, B\}=\{1,4\}$ and the last two give $\{B x z, A y t\}=\{-1,4\}$. Once $A=x+z, B=y+t, B x z$ and Ayt are known, it is easy to find the corresponding values of $x, y, z$ and $t$. The solutions are shown in the following table.
| $A$ | $B$ | Bxz | Ayt | $x, z$ | $y, t$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 4 | -1 | 4 | $\frac{1 \pm \sqrt{2}}{2}$ | 2 |
| 1 | 4 | 4 | -1 | - | - |
| 4 | 1 | -1 | 4 | - | - |
| 4 | 1 | 4 | -1 | 2 | $\frac{1 \pm \sqrt{2}}{2}$ |
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\n17."
}
|
bc2adc95-8c77-5d91-9fca-cd454e397137
| 604,667
|
Determine all positive real numbers $x$ and $y$ satisfying the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}+4=2 \cdot(\sqrt{2 x+1}+\sqrt{2 y+1}) .
$$
|
Answer: $x=y=1+\sqrt{2}$.
Note that
$$
x+\frac{1}{x}+2-2 \sqrt{2 x+1}=\frac{x^{2}+2 x+1-2 x \sqrt{2 x+1}}{x}=\frac{1}{x}(x-\sqrt{2 x+1})^{2} .
$$
Hence the original equation can be rewritten as
$$
\frac{1}{x}(x-\sqrt{2 x+1})^{2}+\frac{1}{y}(y-\sqrt{2 y+1})^{2}=0 .
$$
For $x, y>0$ this gives $x-\sqrt{2 x+1}=0$ and $y-\sqrt{2 y+1}$. It follows that the only solution is $x=y=1+\sqrt{2}$.
|
x=y=1+\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all positive real numbers $x$ and $y$ satisfying the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}+4=2 \cdot(\sqrt{2 x+1}+\sqrt{2 y+1}) .
$$
|
Answer: $x=y=1+\sqrt{2}$.
Note that
$$
x+\frac{1}{x}+2-2 \sqrt{2 x+1}=\frac{x^{2}+2 x+1-2 x \sqrt{2 x+1}}{x}=\frac{1}{x}(x-\sqrt{2 x+1})^{2} .
$$
Hence the original equation can be rewritten as
$$
\frac{1}{x}(x-\sqrt{2 x+1})^{2}+\frac{1}{y}(y-\sqrt{2 y+1})^{2}=0 .
$$
For $x, y>0$ this gives $x-\sqrt{2 x+1}=0$ and $y-\sqrt{2 y+1}$. It follows that the only solution is $x=y=1+\sqrt{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\n18."
}
|
5dc6210f-f243-53d2-8ac3-bcb1d3be3413
| 240,460
|
Let $t \geqslant \frac{1}{2}$ be a real number and $n$ a positive integer. Prove that
$$
t^{2 n} \geqslant(t-1)^{2 n}+(2 t-1)^{n}
$$
|
Use induction. For $n=1$ the inequality reads $t^{2} \geqslant(t-1)^{2}+(2 t-1)$ which is obviously true. To prove the induction step it suffices to show that
$$
t^{2}(t-1)^{2 n}+t^{2}(2 t-1)^{n} \geqslant(t-1)^{2 n+2}+(2 t-1)^{n+1}
$$
This easily follows from $t^{2} \geqslant(t-1)^{2}$ (which is true for $t \geqslant \frac{1}{2}$ ) and $t^{2} \geqslant 2 t-1$ (which is true for any real $t$ ).
Alternative solution. Note that
$$
t^{2 n}=\left(t^{2}\right)^{n}=\left((t-1)^{2}+(2 t-1)\right)^{n} .
$$
Applying the binomial formula to the right-hand side we obtain a sum containing both summands of the right-hand side of the given equality and other summands each of which is clearly non-negative.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $t \geqslant \frac{1}{2}$ be a real number and $n$ a positive integer. Prove that
$$
t^{2 n} \geqslant(t-1)^{2 n}+(2 t-1)^{n}
$$
|
Use induction. For $n=1$ the inequality reads $t^{2} \geqslant(t-1)^{2}+(2 t-1)$ which is obviously true. To prove the induction step it suffices to show that
$$
t^{2}(t-1)^{2 n}+t^{2}(2 t-1)^{n} \geqslant(t-1)^{2 n+2}+(2 t-1)^{n+1}
$$
This easily follows from $t^{2} \geqslant(t-1)^{2}$ (which is true for $t \geqslant \frac{1}{2}$ ) and $t^{2} \geqslant 2 t-1$ (which is true for any real $t$ ).
Alternative solution. Note that
$$
t^{2 n}=\left(t^{2}\right)^{n}=\left((t-1)^{2}+(2 t-1)\right)^{n} .
$$
Applying the binomial formula to the right-hand side we obtain a sum containing both summands of the right-hand side of the given equality and other summands each of which is clearly non-negative.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
ba0bbc8c-5687-5407-8bed-c9787b197e66
| 240,469
|
For every positive integer $n$, let
$$
x_{n}=\frac{(2 n+1) \cdot(2 n+3) \cdots \cdots \cdot(4 n-1) \cdot(4 n+1)}{2 n \cdot(2 n+2) \cdots \cdots \cdot(4 n-2) \cdot 4 n}
$$
Prove that $\frac{1}{4 n}<x_{n}-\sqrt{2}<\frac{2}{n}$.
## Solutions
|
Squaring both sides of the given equality and applying $x(x+2) \leqslant(x+1)^{2}$ to the numerator of the obtained fraction and cancelling we have
$$
x_{n}^{2} \leqslant \frac{(2 n+1) \cdot(4 n+1)}{(2 n)^{2}}<2+\frac{2}{n} .
$$
Similarly (applying $x(x+2) \leqslant(x+1)^{2}$ to the denominator and cancelling) we get
$$
x_{n}^{2} \geqslant \frac{(4 n+1)^{2}}{2 n \cdot 4 n}>2+\frac{1}{n}
$$
Hence
$$
\frac{1}{n}<x_{n}^{2}-2<\frac{2}{n}
$$
and
$$
\frac{1}{n\left(x_{n}+\sqrt{2}\right)}<x_{n}-\sqrt{2}<\frac{2}{n\left(x_{n}+\sqrt{2}\right)} .
$$
From the first chain of inequalities we get $x_{n}>\sqrt{2}$ and $x_{n}<2$. The result then follows from the second chain of inequalities.
Comment. These inequalities can easily be improved. For example, the inequalities in the solution involving $x_{n}^{2}$ can immediately be replaced by $\frac{3}{2 n}<x_{n}^{2}-2<\frac{2}{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For every positive integer $n$, let
$$
x_{n}=\frac{(2 n+1) \cdot(2 n+3) \cdots \cdots \cdot(4 n-1) \cdot(4 n+1)}{2 n \cdot(2 n+2) \cdots \cdots \cdot(4 n-2) \cdot 4 n}
$$
Prove that $\frac{1}{4 n}<x_{n}-\sqrt{2}<\frac{2}{n}$.
## Solutions
|
Squaring both sides of the given equality and applying $x(x+2) \leqslant(x+1)^{2}$ to the numerator of the obtained fraction and cancelling we have
$$
x_{n}^{2} \leqslant \frac{(2 n+1) \cdot(4 n+1)}{(2 n)^{2}}<2+\frac{2}{n} .
$$
Similarly (applying $x(x+2) \leqslant(x+1)^{2}$ to the denominator and cancelling) we get
$$
x_{n}^{2} \geqslant \frac{(4 n+1)^{2}}{2 n \cdot 4 n}>2+\frac{1}{n}
$$
Hence
$$
\frac{1}{n}<x_{n}^{2}-2<\frac{2}{n}
$$
and
$$
\frac{1}{n\left(x_{n}+\sqrt{2}\right)}<x_{n}-\sqrt{2}<\frac{2}{n\left(x_{n}+\sqrt{2}\right)} .
$$
From the first chain of inequalities we get $x_{n}>\sqrt{2}$ and $x_{n}<2$. The result then follows from the second chain of inequalities.
Comment. These inequalities can easily be improved. For example, the inequalities in the solution involving $x_{n}^{2}$ can immediately be replaced by $\frac{3}{2 n}<x_{n}^{2}-2<\frac{2}{n}$.
|
{
"resource_path": "BalticWay/segmented/en-bw00sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\n20."
}
|
06b9399f-8281-5e7e-bf32-2face87ec906
| 604,725
|
A set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the largest possible number of students?
|
Answer: 8 .
Denote the problems by $A, B, C, D, E, F, G, H$, then 8 possible problem sets are $A B C, A D E, A F G, B D G, B F H, C D H, C E F, E G H$. Hence, there could be 8 students.
Suppose that some problem (e.g., $A$ ) was given to 4 students. Then each of these 4 students should receive 2 different "supplementary" problems, and there should be at least 9 problems - a contradiction. Therefore each problem was given to at most 3 students, and there were at most $8 \cdot 3=24$ "awardings" of problems. As each student was "awarded" 3 problems, there were at most 8 students.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A set of 8 problems was prepared for an examination. Each student was given 3 of them. No two students received more than one common problem. What is the largest possible number of students?
|
Answer: 8 .
Denote the problems by $A, B, C, D, E, F, G, H$, then 8 possible problem sets are $A B C, A D E, A F G, B D G, B F H, C D H, C E F, E G H$. Hence, there could be 8 students.
Suppose that some problem (e.g., $A$ ) was given to 4 students. Then each of these 4 students should receive 2 different "supplementary" problems, and there should be at least 9 problems - a contradiction. Therefore each problem was given to at most 3 students, and there were at most $8 \cdot 3=24$ "awardings" of problems. As each student was "awarded" 3 problems, there were at most 8 students.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\n1."
}
|
451ee0af-4e82-564a-808b-85ae07a108ad
| 240,119
|
Let $n \geqslant 2$ be a positive integer. Find whether there exist $n$ pairwise nonintersecting nonempty subsets of $\{1,2,3, \ldots\}$ such that each positive integer can be expressed in a unique way as a sum of at most $n$ integers, all from different subsets.
|
Answer: yes.
Let $A_{1}$ be the set of positive integers whose only non-zero digits may be the 1 -st, the $(n+1)$-st, the $(2 n+1)$-st etc. from the end; $A_{2}$ be the set of positive integers whose only non-zero digits may be the 2 -nd, the $(n+2)$ nd, the $(2 n+2)$-nd etc. from the end, and so on. The sets $A_{1}, A_{2}, \ldots, A_{n}$ have the required property.
Remark. This problem is quite similar to problem 18 from Baltic Way 1997.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n \geqslant 2$ be a positive integer. Find whether there exist $n$ pairwise nonintersecting nonempty subsets of $\{1,2,3, \ldots\}$ such that each positive integer can be expressed in a unique way as a sum of at most $n$ integers, all from different subsets.
|
Answer: yes.
Let $A_{1}$ be the set of positive integers whose only non-zero digits may be the 1 -st, the $(n+1)$-st, the $(2 n+1)$-st etc. from the end; $A_{2}$ be the set of positive integers whose only non-zero digits may be the 2 -nd, the $(n+2)$ nd, the $(2 n+2)$-nd etc. from the end, and so on. The sets $A_{1}, A_{2}, \ldots, A_{n}$ have the required property.
Remark. This problem is quite similar to problem 18 from Baltic Way 1997.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\n2."
}
|
d98e0ca2-5ee3-5220-82f3-6af3cb13b71f
| 240,127
|
The numbers $1,2, \ldots, 49$ are placed in a $7 \times 7$ array, and the sum of the numbers in each row and in each column is computed. Some of these 14 sums are odd while others are even. Let $A$ denote the sum of all the odd sums and $B$ the sum of all even sums. Is it possible that the numbers were placed in the array in such a way that $A=B$ ?
|
Answer: no.
If this were possible, then $2 \cdot(1+\ldots+49)=A+B=2 B$. But $B$ is even since it is the sum of even numbers, whereas $1+\ldots+49=25 \cdot 49$ is odd. This is a contradiction.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The numbers $1,2, \ldots, 49$ are placed in a $7 \times 7$ array, and the sum of the numbers in each row and in each column is computed. Some of these 14 sums are odd while others are even. Let $A$ denote the sum of all the odd sums and $B$ the sum of all even sums. Is it possible that the numbers were placed in the array in such a way that $A=B$ ?
|
Answer: no.
If this were possible, then $2 \cdot(1+\ldots+49)=A+B=2 B$. But $B$ is even since it is the sum of even numbers, whereas $1+\ldots+49=25 \cdot 49$ is odd. This is a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\n3."
}
|
75bcd010-e822-5ee9-ae4d-fc740e9df4b0
| 604,787
|
Let $p$ and $q$ be two different primes. Prove that
$$
\left\lfloor\frac{p}{q}\right\rfloor+\left\lfloor\frac{2 p}{q}\right\rfloor+\left\lfloor\frac{3 p}{q}\right\rfloor+\ldots+\left\lfloor\frac{(q-1) p}{q}\right\rfloor=\frac{1}{2}(p-1)(q-1) .
$$
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
The line $y=\frac{p}{q} x$ contains the diagonal of the rectangle with vertices $(0,0)$, $(q, 0),(q, p)$ and $(0, p)$ and passes through no points with integer coordinates in the interior of that rectangle. For $k=1,2, \ldots, q-1$ the summand $\left\lfloor\frac{k p}{q}\right\rfloor$ counts the number of interior points of the rectangle lying below the diagonal $y=\frac{p}{q} x$ and having $x$-coordinate equal to $k$. Therefore the sum in consideration counts all interior points with integer coordinates below the diagonal, which is exactly half the number of all points with integer coordinates in the interior of the rectangle, i.e. $\frac{1}{2} \cdot(p-1)(q-1)$.
Remark. The integers $p$ and $q$ need not be primes: in the solution we only used the fact that they are coprime.
|
\frac{1}{2}(p-1)(q-1)
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ and $q$ be two different primes. Prove that
$$
\left\lfloor\frac{p}{q}\right\rfloor+\left\lfloor\frac{2 p}{q}\right\rfloor+\left\lfloor\frac{3 p}{q}\right\rfloor+\ldots+\left\lfloor\frac{(q-1) p}{q}\right\rfloor=\frac{1}{2}(p-1)(q-1) .
$$
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
The line $y=\frac{p}{q} x$ contains the diagonal of the rectangle with vertices $(0,0)$, $(q, 0),(q, p)$ and $(0, p)$ and passes through no points with integer coordinates in the interior of that rectangle. For $k=1,2, \ldots, q-1$ the summand $\left\lfloor\frac{k p}{q}\right\rfloor$ counts the number of interior points of the rectangle lying below the diagonal $y=\frac{p}{q} x$ and having $x$-coordinate equal to $k$. Therefore the sum in consideration counts all interior points with integer coordinates below the diagonal, which is exactly half the number of all points with integer coordinates in the interior of the rectangle, i.e. $\frac{1}{2} \cdot(p-1)(q-1)$.
Remark. The integers $p$ and $q$ need not be primes: in the solution we only used the fact that they are coprime.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\n4."
}
|
eb9b2db1-9359-5400-b7e1-115f08fb2e03
| 604,799
|
Let 2001 given points on a circle be colored either red or green. In one step all points are recolored simultaneously in the following way: If both direct neighbors of a point $P$ have the same color as $P$, then the color of $P$ remains unchanged, otherwise $P$ obtains the other color. Starting with the first coloring $F_{1}$, we obtain the colorings $F_{2}, F_{3}, \ldots$ after several recoloring steps. Prove that there is a number $n_{0} \leqslant 1000$ such that $F_{n_{0}}=F_{n_{0}+2}$. Is the assertion also true if 1000 is replaced by 999 ?
|
Answer: no.
Let the points be denoted by $1,2, \ldots, 2001$ such that $i, j$ are neighbors if $|i-j|=1$ or $\{i, j\}=\{1,2001\}$. We say that $k$ points form a monochromatic segment of length $k$ if the points are consecutive on the circle and if
they all have the same color. For a coloring $F$ let $d(F)$ be the maximum length of a monochromatic segment. Note that $d\left(F_{n}\right)>1$ for all $n$ since 2001 is odd. If $d\left(F_{1}\right)=2001$ then all points have the same color, hence $F_{1}=F_{2}=F_{3}=\ldots$ and we can choose $n_{0}=1$. Thus, let $1<d\left(F_{1}\right)<2001$. Below we shall prove the following implications:
If $3<d\left(F_{n}\right)<2001$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)-2 ;$
If $d\left(F_{n}\right)=3$, then $d\left(F_{n+1}\right)=2$;
If $d\left(F_{n}\right)=2$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)$ and $F_{n+2}=F_{n}$;
From (1) and (2) it follows that $d\left(F_{1000}\right) \leqslant 2$, hence by (3) we have $F_{1000}=F_{1002}$. Moreover, if $F_{1}$ is the coloring where 1 is colored red and all other points are colored green, then $d\left(F_{1}\right)=2000$ and thus $d\left(F_{1}\right)>d\left(F_{2}\right)>\ldots>d\left(F_{1000}\right)=2$ which shows that, for all $n<1000, F_{n} \neq F_{n+2}$ and thus 1000 cannot be replaced by 999 .
It remains to prove (1)-(3). Let $(i+1, \ldots, i+k)$ be a longest monochromatic segment for $F_{n}$ (considering the labels of the points modulo 2001). Then $(i+2, \ldots, i+k-1)$ is a monochromatic segment for $F_{n+1}$ and thus $d\left(F_{n+1}\right) \geqslant d\left(F_{n}\right)-2$. Moreover, if $(i+1, \ldots, i+k)$ is a longest monochromatic segment for $F_{n+1}$ where $k \geqslant 3$, then $(i, \ldots, i+k+1)$ is a monochromatic segment for $F_{n}$. From this and $F_{n+1}>1$ the implications (1) and (2) clearly follow. For proof of (3) note that if $d\left(F_{n}\right) \leqslant 2$ then $F_{n+1}$ is obtained from $F_{n}$ by changing the colour of all points.
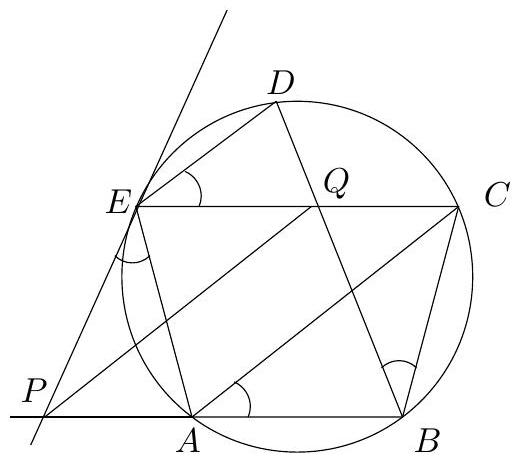
Figure 1
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let 2001 given points on a circle be colored either red or green. In one step all points are recolored simultaneously in the following way: If both direct neighbors of a point $P$ have the same color as $P$, then the color of $P$ remains unchanged, otherwise $P$ obtains the other color. Starting with the first coloring $F_{1}$, we obtain the colorings $F_{2}, F_{3}, \ldots$ after several recoloring steps. Prove that there is a number $n_{0} \leqslant 1000$ such that $F_{n_{0}}=F_{n_{0}+2}$. Is the assertion also true if 1000 is replaced by 999 ?
|
Answer: no.
Let the points be denoted by $1,2, \ldots, 2001$ such that $i, j$ are neighbors if $|i-j|=1$ or $\{i, j\}=\{1,2001\}$. We say that $k$ points form a monochromatic segment of length $k$ if the points are consecutive on the circle and if
they all have the same color. For a coloring $F$ let $d(F)$ be the maximum length of a monochromatic segment. Note that $d\left(F_{n}\right)>1$ for all $n$ since 2001 is odd. If $d\left(F_{1}\right)=2001$ then all points have the same color, hence $F_{1}=F_{2}=F_{3}=\ldots$ and we can choose $n_{0}=1$. Thus, let $1<d\left(F_{1}\right)<2001$. Below we shall prove the following implications:
If $3<d\left(F_{n}\right)<2001$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)-2 ;$
If $d\left(F_{n}\right)=3$, then $d\left(F_{n+1}\right)=2$;
If $d\left(F_{n}\right)=2$, then $d\left(F_{n+1}\right)=d\left(F_{n}\right)$ and $F_{n+2}=F_{n}$;
From (1) and (2) it follows that $d\left(F_{1000}\right) \leqslant 2$, hence by (3) we have $F_{1000}=F_{1002}$. Moreover, if $F_{1}$ is the coloring where 1 is colored red and all other points are colored green, then $d\left(F_{1}\right)=2000$ and thus $d\left(F_{1}\right)>d\left(F_{2}\right)>\ldots>d\left(F_{1000}\right)=2$ which shows that, for all $n<1000, F_{n} \neq F_{n+2}$ and thus 1000 cannot be replaced by 999 .
It remains to prove (1)-(3). Let $(i+1, \ldots, i+k)$ be a longest monochromatic segment for $F_{n}$ (considering the labels of the points modulo 2001). Then $(i+2, \ldots, i+k-1)$ is a monochromatic segment for $F_{n+1}$ and thus $d\left(F_{n+1}\right) \geqslant d\left(F_{n}\right)-2$. Moreover, if $(i+1, \ldots, i+k)$ is a longest monochromatic segment for $F_{n+1}$ where $k \geqslant 3$, then $(i, \ldots, i+k+1)$ is a monochromatic segment for $F_{n}$. From this and $F_{n+1}>1$ the implications (1) and (2) clearly follow. For proof of (3) note that if $d\left(F_{n}\right) \leqslant 2$ then $F_{n+1}$ is obtained from $F_{n}$ by changing the colour of all points.

Figure 1
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\n5."
}
|
7812cc1b-fd27-5495-9224-bcedfb25bad7
| 240,155
|
The points $A, B, C, D, E$ lie on the circle $c$ in this order and satisfy $A B \| E C$ and $A C \| E D$. The line tangent to the circle $c$ at $E$ meets the line $A B$ at $P$. The lines $B D$ and $E C$ meet at $Q$. Prove that $|A C|=|P Q|$.
|
The arcs $B C$ and $A E$ are of equal length (see Figure 1). Also, since
$A B \| E C$ and $E D \| A C$, we have $\angle C A B=\angle D E C$ and the $\operatorname{arcs} D C$ and $B C$ are of equal length. Since $P E$ is tangent to $c$ and $|A E|=|D C|$, then $\angle P E A=\angle D B C=\angle Q B C$. As $A B C D$ is inscribed in $c$, we have $\angle Q C B=180^{\circ}-\angle E A B=\angle P A E$. Also, $A B C D$ is an isosceles trapezium, whence $|A E|=|B C|$. So the triangles $A P E$ and $C Q B$ are congruent, and $|Q C|=|P A|$. Now $P A C Q$ is a quadrilateral with a pair of opposite sides equal and parallel. So $P A C Q$ is a parallelogram, and $|P Q|=|A C|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The points $A, B, C, D, E$ lie on the circle $c$ in this order and satisfy $A B \| E C$ and $A C \| E D$. The line tangent to the circle $c$ at $E$ meets the line $A B$ at $P$. The lines $B D$ and $E C$ meet at $Q$. Prove that $|A C|=|P Q|$.
|
The arcs $B C$ and $A E$ are of equal length (see Figure 1). Also, since
$A B \| E C$ and $E D \| A C$, we have $\angle C A B=\angle D E C$ and the $\operatorname{arcs} D C$ and $B C$ are of equal length. Since $P E$ is tangent to $c$ and $|A E|=|D C|$, then $\angle P E A=\angle D B C=\angle Q B C$. As $A B C D$ is inscribed in $c$, we have $\angle Q C B=180^{\circ}-\angle E A B=\angle P A E$. Also, $A B C D$ is an isosceles trapezium, whence $|A E|=|B C|$. So the triangles $A P E$ and $C Q B$ are congruent, and $|Q C|=|P A|$. Now $P A C Q$ is a quadrilateral with a pair of opposite sides equal and parallel. So $P A C Q$ is a parallelogram, and $|P Q|=|A C|$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\n6."
}
|
74b12f75-041c-58c1-b8f1-3bf455b08a5c
| 240,165
|
Given a parallelogram $A B C D$. A circle passing through $A$ meets the line segments $A B, A C$ and $A D$ at inner points $M, K, N$, respectively. Prove that
$$
|A B| \cdot|A M|+|A D| \cdot|A N|=|A K| \cdot|A C| .
$$
|
Let $X$ be the point on segment $A C$ such that $\angle A D X=\angle A K N$, then
$$
\angle A X D=\angle A N K=180^{\circ}-\angle A M K
$$
(see Figure 2). Triangles $N A K$ and $X A D$ are similar, having two pairs of equal angles, hence $|A X|=\frac{|A N| \cdot|A D|}{|A K|}$. Since triangles $M A K$ and $X C D$ are also similar, we have $|C X|=\frac{|A M| \cdot|C D|}{|A K|}=\frac{|A M| \cdot|A B|}{|A K|}$ and
$$
|A M| \cdot|A B|+|A N| \cdot|A D|=(|A X|+|C X|) \cdot|A K|=|A C| \cdot|A K| \text {. }
$$
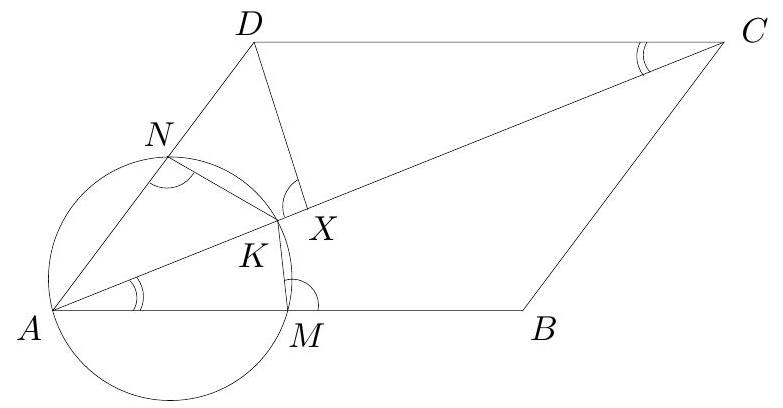
Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Given a parallelogram $A B C D$. A circle passing through $A$ meets the line segments $A B, A C$ and $A D$ at inner points $M, K, N$, respectively. Prove that
$$
|A B| \cdot|A M|+|A D| \cdot|A N|=|A K| \cdot|A C| .
$$
|
Let $X$ be the point on segment $A C$ such that $\angle A D X=\angle A K N$, then
$$
\angle A X D=\angle A N K=180^{\circ}-\angle A M K
$$
(see Figure 2). Triangles $N A K$ and $X A D$ are similar, having two pairs of equal angles, hence $|A X|=\frac{|A N| \cdot|A D|}{|A K|}$. Since triangles $M A K$ and $X C D$ are also similar, we have $|C X|=\frac{|A M| \cdot|C D|}{|A K|}=\frac{|A M| \cdot|A B|}{|A K|}$ and
$$
|A M| \cdot|A B|+|A N| \cdot|A D|=(|A X|+|C X|) \cdot|A K|=|A C| \cdot|A K| \text {. }
$$

Figure 2
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\n7."
}
|
1373c768-91aa-5100-973f-41893999c926
| 240,174
|
Let $A B C D$ be a convex quadrilateral, and let $N$ be the midpoint of $B C$. Suppose further that $\angle A N D=135^{\circ}$. Prove that
$$
|A B|+|C D|+\frac{1}{\sqrt{2}} \cdot|B C| \geqslant|A D|
$$
|
Let $X$ be the point symmetric to $B$ with respect to $A N$, and let $Y$ be the point symmetric to $C$ with respect to $D N$ (see Figure 3 ). Then
$$
\angle X N Y=180^{\circ}-2 \cdot\left(180^{\circ}-135^{\circ}\right)=90^{\circ}
$$
and $|N X|=|N Y|=\frac{|B C|}{2}$. Therefore, $|X Y|=\frac{|B C|}{\sqrt{2}}$. Moreover, we have
$$
\begin{aligned}
& |A X|=|A B| \text { and }|D Y|=|D C| \text {. Consequently, } \\
& \qquad|A D| \leqslant|A X|+|X Y|+|Y D|=|A B|+\frac{|B C|}{\sqrt{2}}+|D C| .
\end{aligned}
$$
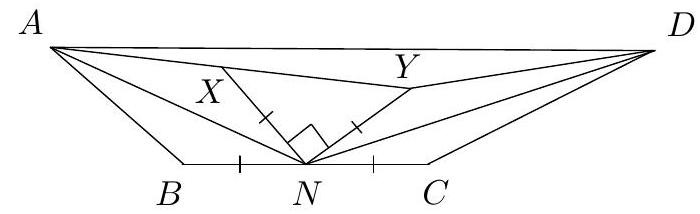
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C D$ be a convex quadrilateral, and let $N$ be the midpoint of $B C$. Suppose further that $\angle A N D=135^{\circ}$. Prove that
$$
|A B|+|C D|+\frac{1}{\sqrt{2}} \cdot|B C| \geqslant|A D|
$$
|
Let $X$ be the point symmetric to $B$ with respect to $A N$, and let $Y$ be the point symmetric to $C$ with respect to $D N$ (see Figure 3 ). Then
$$
\angle X N Y=180^{\circ}-2 \cdot\left(180^{\circ}-135^{\circ}\right)=90^{\circ}
$$
and $|N X|=|N Y|=\frac{|B C|}{2}$. Therefore, $|X Y|=\frac{|B C|}{\sqrt{2}}$. Moreover, we have
$$
\begin{aligned}
& |A X|=|A B| \text { and }|D Y|=|D C| \text {. Consequently, } \\
& \qquad|A D| \leqslant|A X|+|X Y|+|Y D|=|A B|+\frac{|B C|}{\sqrt{2}}+|D C| .
\end{aligned}
$$

Figure 3
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\n8."
}
|
3727d9f6-f8eb-55ad-a10e-3b26dd3fd3d3
| 240,183
|
Given a rhombus $A B C D$, find the locus of the points $P$ lying inside the rhombus and satisfying $\angle A P D+\angle B P C=180^{\circ}$.
|
Answer: the locus of the points $P$ is the union of the diagonals $A C$ and $B D$.
Let $Q$ be a point such that $P Q C D$ is a parallelogram (see Figure 4). Then $A B Q P$ is also a parallelogram. From the equality $\angle A P D+\angle B P C=180^{\circ}$ it follows that $\angle B Q C+\angle B P C=180^{\circ}$, so the points $B, Q, C, P$ lie on a common circle. Therefore, $\angle P B C=\angle P Q C=\angle P D C$, and since $|B C|=|C D|$, we obtain that $\angle C P B=\angle C P D$ or $\angle C P B+\angle C P D=180^{\circ}$. Hence, the point $P$ lies on the segment $A C$ or on the segment $B D$.
Figure 4
Conversely, any point $P$ lying on the diagonal $A C$ satisfies the equation $\angle B P C=\angle D P C$. Therefore, $\angle A P D+\angle B P C=180^{\circ}$. Analogously, we show that the last equation holds if the point $P$ lies on the diagonal $B D$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Given a rhombus $A B C D$, find the locus of the points $P$ lying inside the rhombus and satisfying $\angle A P D+\angle B P C=180^{\circ}$.
|
Answer: the locus of the points $P$ is the union of the diagonals $A C$ and $B D$.
Let $Q$ be a point such that $P Q C D$ is a parallelogram (see Figure 4). Then $A B Q P$ is also a parallelogram. From the equality $\angle A P D+\angle B P C=180^{\circ}$ it follows that $\angle B Q C+\angle B P C=180^{\circ}$, so the points $B, Q, C, P$ lie on a common circle. Therefore, $\angle P B C=\angle P Q C=\angle P D C$, and since $|B C|=|C D|$, we obtain that $\angle C P B=\angle C P D$ or $\angle C P B+\angle C P D=180^{\circ}$. Hence, the point $P$ lies on the segment $A C$ or on the segment $B D$.

Figure 4
Conversely, any point $P$ lying on the diagonal $A C$ satisfies the equation $\angle B P C=\angle D P C$. Therefore, $\angle A P D+\angle B P C=180^{\circ}$. Analogously, we show that the last equation holds if the point $P$ lies on the diagonal $B D$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\n9."
}
|
838d59e6-dcb2-5f5b-b61d-7a06589611dd
| 604,904
|
In a triangle $A B C$, the bisector of $\angle B A C$ meets the side $B C$ at the point $D$. Knowing that $|B D| \cdot|C D|=|A D|^{2}$ and $\angle A D B=45^{\circ}$, determine the angles of triangle $A B C$.
|
Answer: $\angle B A C=60^{\circ}, \angle A B C=105^{\circ}$ and $\angle A C B=15^{\circ}$.
Suppose the line $A D$ meets the circumcircle of triangle $A B C$ at $A$ and $E$ (see Figure 5). Let $M$ be the midpoint of $B C$ and $O$ the circumcentre of triangle $A B C$. Since the arcs $B E$ and $E C$ are equal, then the points $O$, $M, E$ are collinear and $O E$ is perpendicular to $B C$. From the equality
$\angle C D E=\angle A D B=45^{\circ}$ it follows that $\angle A E O=45^{\circ}$. Since $|A O|=|E O|$, we have $\angle A O E=90^{\circ}$ and $A O \| D M$.
From the equality $|B D| \cdot|C D|=|A D|^{2}$ we obtain $|A D|=|D E|$, which implies that $|O M|=|M E|$. Therefore $|B O|=|B E|$ and also $|B O|=|E O|$. Hence the triangle $B O E$ is equilateral. This gives $\angle B A E=30^{\circ}$, so $\angle B A C=60^{\circ}$. Summing up the angles of the triangle $A B D$ we obtain $\angle A B C=105^{\circ}$ and from this $\angle A C B=15^{\circ}$.
Figure 5
|
\angle B A C=60^{\circ}, \angle A B C=105^{\circ}, \angle A C B=15^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In a triangle $A B C$, the bisector of $\angle B A C$ meets the side $B C$ at the point $D$. Knowing that $|B D| \cdot|C D|=|A D|^{2}$ and $\angle A D B=45^{\circ}$, determine the angles of triangle $A B C$.
|
Answer: $\angle B A C=60^{\circ}, \angle A B C=105^{\circ}$ and $\angle A C B=15^{\circ}$.
Suppose the line $A D$ meets the circumcircle of triangle $A B C$ at $A$ and $E$ (see Figure 5). Let $M$ be the midpoint of $B C$ and $O$ the circumcentre of triangle $A B C$. Since the arcs $B E$ and $E C$ are equal, then the points $O$, $M, E$ are collinear and $O E$ is perpendicular to $B C$. From the equality
$\angle C D E=\angle A D B=45^{\circ}$ it follows that $\angle A E O=45^{\circ}$. Since $|A O|=|E O|$, we have $\angle A O E=90^{\circ}$ and $A O \| D M$.
From the equality $|B D| \cdot|C D|=|A D|^{2}$ we obtain $|A D|=|D E|$, which implies that $|O M|=|M E|$. Therefore $|B O|=|B E|$ and also $|B O|=|E O|$. Hence the triangle $B O E$ is equilateral. This gives $\angle B A E=30^{\circ}$, so $\angle B A C=60^{\circ}$. Summing up the angles of the triangle $A B D$ we obtain $\angle A B C=105^{\circ}$ and from this $\angle A C B=15^{\circ}$.

Figure 5
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\n10."
}
|
0eafb1e5-37e8-5474-851d-a7d038b381fb
| 240,202
|
The real-valued function $f$ is defined for all positive integers. For any integers $a>1, b>1$ with $d=\operatorname{gcd}(a, b)$, we have
$$
f(a b)=f(d) \cdot\left(f\left(\frac{a}{d}\right)+f\left(\frac{b}{d}\right)\right),
$$
Determine all possible values of $f(2001)$.
|
Answer: 0 and $\frac{1}{2}$.
Obviously the constant functions $f(n)=0$ and $f(n)=\frac{1}{2}$ provide solutions.
We show that there are no other solutions. Assume $f(2001) \neq 0$. Since $2001=3 \cdot 667$ and $\operatorname{gcd}(3,667)=1$, then
$$
f(2001)=f(1) \cdot(f(3)+f(667)),
$$
and $f(1) \neq 0$. Since $\operatorname{gcd}(2001,2001)=2001$ then
$$
f\left(2001^{2}\right)=f(2001)(2 \cdot f(1)) \neq 0 .
$$
Also $\operatorname{gcd}\left(2001,2001^{3}\right)=2001$, so
$$
f\left(2001^{4}\right)=f(2001) \cdot\left(f(1)+f\left(2001^{2}\right)\right)=f(1) f(2001)(1+2 f(2001))
$$
On the other hand, $\operatorname{gcd}\left(2001^{2}, 2001^{2}\right)=2001^{2}$ and
$$
f\left(2001^{4}\right)=f\left(2001^{2}\right) \cdot(f(1)+f(1))=2 f(1) f\left(2001^{2}\right)=4 f(1)^{2} f(2001) .
$$
So $4 f(1)=1+2 f(2001)$ and $f(2001)=2 f(1)-\frac{1}{2}$. Exactly the same
argument starting from $f\left(2001^{2}\right) \neq 0$ instead of $f(2001)$ shows that $f\left(2001^{2}\right)=2 f(1)-\frac{1}{2}$. So
$$
2 f(1)-\frac{1}{2}=2 f(1)\left(2 f(1)-\frac{1}{2}\right) \text {. }
$$
Since $2 f(1)-\frac{1}{2}=f(2001) \neq 0$, we have $f(1)=\frac{1}{2}$, which implies $f(2001)=2 f(1)-\frac{1}{2}=\frac{1}{2}$.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The real-valued function $f$ is defined for all positive integers. For any integers $a>1, b>1$ with $d=\operatorname{gcd}(a, b)$, we have
$$
f(a b)=f(d) \cdot\left(f\left(\frac{a}{d}\right)+f\left(\frac{b}{d}\right)\right),
$$
Determine all possible values of $f(2001)$.
|
Answer: 0 and $\frac{1}{2}$.
Obviously the constant functions $f(n)=0$ and $f(n)=\frac{1}{2}$ provide solutions.
We show that there are no other solutions. Assume $f(2001) \neq 0$. Since $2001=3 \cdot 667$ and $\operatorname{gcd}(3,667)=1$, then
$$
f(2001)=f(1) \cdot(f(3)+f(667)),
$$
and $f(1) \neq 0$. Since $\operatorname{gcd}(2001,2001)=2001$ then
$$
f\left(2001^{2}\right)=f(2001)(2 \cdot f(1)) \neq 0 .
$$
Also $\operatorname{gcd}\left(2001,2001^{3}\right)=2001$, so
$$
f\left(2001^{4}\right)=f(2001) \cdot\left(f(1)+f\left(2001^{2}\right)\right)=f(1) f(2001)(1+2 f(2001))
$$
On the other hand, $\operatorname{gcd}\left(2001^{2}, 2001^{2}\right)=2001^{2}$ and
$$
f\left(2001^{4}\right)=f\left(2001^{2}\right) \cdot(f(1)+f(1))=2 f(1) f\left(2001^{2}\right)=4 f(1)^{2} f(2001) .
$$
So $4 f(1)=1+2 f(2001)$ and $f(2001)=2 f(1)-\frac{1}{2}$. Exactly the same
argument starting from $f\left(2001^{2}\right) \neq 0$ instead of $f(2001)$ shows that $f\left(2001^{2}\right)=2 f(1)-\frac{1}{2}$. So
$$
2 f(1)-\frac{1}{2}=2 f(1)\left(2 f(1)-\frac{1}{2}\right) \text {. }
$$
Since $2 f(1)-\frac{1}{2}=f(2001) \neq 0$, we have $f(1)=\frac{1}{2}$, which implies $f(2001)=2 f(1)-\frac{1}{2}=\frac{1}{2}$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\n11."
}
|
316d3633-64b3-5913-a882-033261197b3b
| 240,211
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $\sum_{i=1}^{n} a_{i}^{3}=3$ and $\sum_{i=1}^{n} a_{i}^{5}=5$. Prove that $\sum_{i=1}^{n} a_{i}>\frac{3}{2}$.
|
By Hölder's inequality,
$$
\sum_{i=1}^{n} a^{3}=\sum_{i=1}^{n}\left(a_{i} \cdot a_{i}^{2}\right) \leqslant\left(\sum_{i=1}^{n} a_{i}^{5 / 3}\right)^{3 / 5} \cdot\left(\sum_{i=1}^{n}\left(a_{i}^{2}\right)^{5 / 2}\right)^{2 / 5} .
$$
We will show that
$$
\sum_{i=1}^{n} a_{i}^{5 / 3} \leqslant\left(\sum_{i=1}^{n} a_{i}\right)^{5 / 3}
$$
Let $S=\sum_{i=1}^{n} a_{i}$, then (4) is equivalent to
$$
\sum_{i=1}^{n}\left(\frac{a_{i}}{S}\right)^{5 / 3} \leqslant 1=\sum_{i=1}^{n} \frac{a_{i}}{S}
$$
which holds since $0<\frac{a_{i}}{S} \leqslant 1$ and $\frac{5}{3}>1$ yield $\left(\frac{a_{i}}{S}\right)^{5 / 3} \leqslant \frac{a_{i}}{S}$. So,
$$
\sum_{i=1}^{n} a_{i}^{3} \leqslant\left(\sum_{i=1}^{n} a_{i}\right) \cdot\left(\sum_{i=1}^{n} a_{i}^{5}\right)^{2 / 5}
$$
which gives $\sum_{i=1}^{n} a_{i} \geqslant \frac{3}{5^{2 / 5}}>\frac{3}{2}$, since $2^{5}>5^{2}$ and hence $2>5^{2 / 5}$.
|
\sum_{i=1}^{n} a_{i} > \frac{3}{2}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $\sum_{i=1}^{n} a_{i}^{3}=3$ and $\sum_{i=1}^{n} a_{i}^{5}=5$. Prove that $\sum_{i=1}^{n} a_{i}>\frac{3}{2}$.
|
By Hölder's inequality,
$$
\sum_{i=1}^{n} a^{3}=\sum_{i=1}^{n}\left(a_{i} \cdot a_{i}^{2}\right) \leqslant\left(\sum_{i=1}^{n} a_{i}^{5 / 3}\right)^{3 / 5} \cdot\left(\sum_{i=1}^{n}\left(a_{i}^{2}\right)^{5 / 2}\right)^{2 / 5} .
$$
We will show that
$$
\sum_{i=1}^{n} a_{i}^{5 / 3} \leqslant\left(\sum_{i=1}^{n} a_{i}\right)^{5 / 3}
$$
Let $S=\sum_{i=1}^{n} a_{i}$, then (4) is equivalent to
$$
\sum_{i=1}^{n}\left(\frac{a_{i}}{S}\right)^{5 / 3} \leqslant 1=\sum_{i=1}^{n} \frac{a_{i}}{S}
$$
which holds since $0<\frac{a_{i}}{S} \leqslant 1$ and $\frac{5}{3}>1$ yield $\left(\frac{a_{i}}{S}\right)^{5 / 3} \leqslant \frac{a_{i}}{S}$. So,
$$
\sum_{i=1}^{n} a_{i}^{3} \leqslant\left(\sum_{i=1}^{n} a_{i}\right) \cdot\left(\sum_{i=1}^{n} a_{i}^{5}\right)^{2 / 5}
$$
which gives $\sum_{i=1}^{n} a_{i} \geqslant \frac{3}{5^{2 / 5}}>\frac{3}{2}$, since $2^{5}>5^{2}$ and hence $2>5^{2 / 5}$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\n12."
}
|
5cfff66a-6927-5cb6-8dad-0742ab12ea39
| 240,219
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers satisfying $a_{0}=1$ and $a_{n}=a_{\lfloor 7 n / 9\rfloor}+a_{\lfloor n / 9\rfloor}$ for $n=1,2, \ldots$ Prove that there exists a positive integer $k$ with $a_{k}<\frac{k}{2001 !}$.
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
Consider the equation
$$
\left(\frac{7}{9}\right)^{x}+\left(\frac{1}{9}\right)^{x}=1 .
$$
It has a root $\frac{1}{2}<\alpha<1$, because $\sqrt{\frac{7}{9}}+\sqrt{\frac{1}{9}}=\frac{\sqrt{7}+1}{3}>1$ and $\frac{7}{9}+\frac{1}{9}<1$. We will prove that $a_{n} \leqslant M \cdot n^{\alpha}$ for some $M>0-$ since $\frac{n^{\alpha}}{n}$ will be arbitrarily small for large enough $n$, the claim follows from this immediately. We choose $M$ so that the inequality $a_{n} \leqslant M \cdot n^{\alpha}$ holds for $1 \leqslant n \leqslant 8$; since for $n \geqslant 9$ we have $1<[7 n / 9]<n$ and $1 \leqslant[n / 9]<n$, it follows by induction that
$$
\begin{aligned}
a_{n} & =a_{[7 n / 9]}+a_{[n / 9]} \leqslant M \cdot\left[\frac{7 n}{9}\right]^{\alpha}+M \cdot\left[\frac{n}{9}\right]^{\alpha} \leqslant \\
& \leqslant M \cdot\left(\frac{7 n}{9}\right)^{\alpha}+M \cdot\left(\frac{n}{9}\right)^{\alpha}=M \cdot n^{\alpha} \cdot\left(\left(\frac{7}{9}\right)^{\alpha}+\left(\frac{1}{9}\right)^{\alpha}\right)=M \cdot n^{\alpha} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of real numbers satisfying $a_{0}=1$ and $a_{n}=a_{\lfloor 7 n / 9\rfloor}+a_{\lfloor n / 9\rfloor}$ for $n=1,2, \ldots$ Prove that there exists a positive integer $k$ with $a_{k}<\frac{k}{2001 !}$.
(Here $\lfloor x\rfloor$ denotes the largest integer not greater than $x$.)
|
Consider the equation
$$
\left(\frac{7}{9}\right)^{x}+\left(\frac{1}{9}\right)^{x}=1 .
$$
It has a root $\frac{1}{2}<\alpha<1$, because $\sqrt{\frac{7}{9}}+\sqrt{\frac{1}{9}}=\frac{\sqrt{7}+1}{3}>1$ and $\frac{7}{9}+\frac{1}{9}<1$. We will prove that $a_{n} \leqslant M \cdot n^{\alpha}$ for some $M>0-$ since $\frac{n^{\alpha}}{n}$ will be arbitrarily small for large enough $n$, the claim follows from this immediately. We choose $M$ so that the inequality $a_{n} \leqslant M \cdot n^{\alpha}$ holds for $1 \leqslant n \leqslant 8$; since for $n \geqslant 9$ we have $1<[7 n / 9]<n$ and $1 \leqslant[n / 9]<n$, it follows by induction that
$$
\begin{aligned}
a_{n} & =a_{[7 n / 9]}+a_{[n / 9]} \leqslant M \cdot\left[\frac{7 n}{9}\right]^{\alpha}+M \cdot\left[\frac{n}{9}\right]^{\alpha} \leqslant \\
& \leqslant M \cdot\left(\frac{7 n}{9}\right)^{\alpha}+M \cdot\left(\frac{n}{9}\right)^{\alpha}=M \cdot n^{\alpha} \cdot\left(\left(\frac{7}{9}\right)^{\alpha}+\left(\frac{1}{9}\right)^{\alpha}\right)=M \cdot n^{\alpha} .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\n13."
}
|
8056fe7e-4998-57fc-b0a2-431e6d47a783
| 240,230
|
There are $2 n$ cards. On each card some real number $x, 1 \leqslant x \leqslant 2$, is written (there can be different numbers on different cards). Prove that
the cards can be divided into two heaps with sums $s_{1}$ and $s_{2}$ so that $\frac{n}{n+1} \leqslant \frac{s_{1}}{s_{2}} \leqslant 1$.
|
Let the numbers be $x_{1} \leqslant x_{2} \leqslant \ldots \leqslant x_{2 n-1} \leqslant x_{2 n}$. We will show that the choice $s_{1}=x_{1}+x_{3}+x_{5}+\cdots+x_{2 n-1}$ and $s_{2}=x_{2}+x_{4}+\cdots+x_{2 n}$ solves the problem. Indeed, the inequality $\frac{s_{1}}{s_{2}} \leqslant 1$ is obvious and we have
$$
\begin{aligned}
\frac{s_{1}}{s_{2}} & =\frac{x_{1}+x_{3}+x_{5}+\ldots+x_{2 n-1}}{x_{2}+x_{4}+x_{6}+\ldots+x_{2 n}}=\frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+x_{1}}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+x_{2 n}} \geqslant \\
& \geqslant \frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant \frac{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2}= \\
& =1-\frac{1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant 1-\frac{1}{(n-1)+2}=\frac{n}{n+1} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are $2 n$ cards. On each card some real number $x, 1 \leqslant x \leqslant 2$, is written (there can be different numbers on different cards). Prove that
the cards can be divided into two heaps with sums $s_{1}$ and $s_{2}$ so that $\frac{n}{n+1} \leqslant \frac{s_{1}}{s_{2}} \leqslant 1$.
|
Let the numbers be $x_{1} \leqslant x_{2} \leqslant \ldots \leqslant x_{2 n-1} \leqslant x_{2 n}$. We will show that the choice $s_{1}=x_{1}+x_{3}+x_{5}+\cdots+x_{2 n-1}$ and $s_{2}=x_{2}+x_{4}+\cdots+x_{2 n}$ solves the problem. Indeed, the inequality $\frac{s_{1}}{s_{2}} \leqslant 1$ is obvious and we have
$$
\begin{aligned}
\frac{s_{1}}{s_{2}} & =\frac{x_{1}+x_{3}+x_{5}+\ldots+x_{2 n-1}}{x_{2}+x_{4}+x_{6}+\ldots+x_{2 n}}=\frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+x_{1}}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+x_{2 n}} \geqslant \\
& \geqslant \frac{\left(x_{3}+x_{5}+\ldots+x_{2 n-1}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant \frac{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2}= \\
& =1-\frac{1}{\left(x_{2}+x_{4}+\ldots+x_{2 n-2}\right)+2} \geqslant 1-\frac{1}{(n-1)+2}=\frac{n}{n+1} .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\n14."
}
|
c0cdf51a-0bc8-58be-95b3-c7e189329c62
| 240,239
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive real numbers satisfying $i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i-1} a_{i+1}$ for $i=1,2, \ldots$ Furthermore, let $x$ and $y$ be positive reals, and let $b_{i}=x a_{i}+y a_{i-1}$ for $i=1,2, \ldots$ Prove that the inequality $i \cdot b_{i}^{2}>(i+1) \cdot b_{i-1} b_{i+1}$ holds for all integers $i \geqslant 2$.
|
Let $i \geqslant 2$. We are given the inequalities
$$
(i-1) \cdot a_{i-1}^{2} \geqslant i \cdot a_{i} a_{i-2}
$$
and
$$
i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i+1} a_{i-1} .
$$
Multiplying both sides of (6) by $x^{2}$, we obtain
$$
i \cdot x^{2} \cdot a_{i}^{2} \geqslant(i+1) \cdot x^{2} \cdot a_{i+1} a_{i-1}
$$
By (5),
$$
\frac{a_{i-1}^{2}}{a_{i} a_{i-2}} \geqslant \frac{i}{i-1}=1+\frac{1}{i-1}>1+\frac{1}{i}=\frac{i+1}{i}
$$
which implies
$$
i \cdot y^{2} \cdot a_{i-1}^{2}>(i+1) \cdot y^{2} \cdot a_{i} a_{i-2} .
$$
Multiplying (5) and (6), and dividing both sides of the resulting inequality by $i a_{i} a_{i-1}$, we get
$$
(i-1) \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot a_{i+1} a_{i-2} .
$$
Adding $(i+1) a_{i} a_{i-1}$ to both sides of the last inequality and multiplying both sides of the resulting inequality by $x y$ gives
$$
i \cdot 2 x y \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot x y \cdot\left(a_{i+1} a_{i-2}+a_{i} a_{i-1}\right) .
$$
Finally, adding up (7), (8) and (9) results in
$$
i \cdot\left(x a_{i}+y a_{i-1}\right)^{2}>(i+1) \cdot\left(x a_{i+1}+y a_{i}\right)\left(x a_{i-1}+y a_{i-2}\right)
$$
which is equivalent to the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of positive real numbers satisfying $i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i-1} a_{i+1}$ for $i=1,2, \ldots$ Furthermore, let $x$ and $y$ be positive reals, and let $b_{i}=x a_{i}+y a_{i-1}$ for $i=1,2, \ldots$ Prove that the inequality $i \cdot b_{i}^{2}>(i+1) \cdot b_{i-1} b_{i+1}$ holds for all integers $i \geqslant 2$.
|
Let $i \geqslant 2$. We are given the inequalities
$$
(i-1) \cdot a_{i-1}^{2} \geqslant i \cdot a_{i} a_{i-2}
$$
and
$$
i \cdot a_{i}^{2} \geqslant(i+1) \cdot a_{i+1} a_{i-1} .
$$
Multiplying both sides of (6) by $x^{2}$, we obtain
$$
i \cdot x^{2} \cdot a_{i}^{2} \geqslant(i+1) \cdot x^{2} \cdot a_{i+1} a_{i-1}
$$
By (5),
$$
\frac{a_{i-1}^{2}}{a_{i} a_{i-2}} \geqslant \frac{i}{i-1}=1+\frac{1}{i-1}>1+\frac{1}{i}=\frac{i+1}{i}
$$
which implies
$$
i \cdot y^{2} \cdot a_{i-1}^{2}>(i+1) \cdot y^{2} \cdot a_{i} a_{i-2} .
$$
Multiplying (5) and (6), and dividing both sides of the resulting inequality by $i a_{i} a_{i-1}$, we get
$$
(i-1) \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot a_{i+1} a_{i-2} .
$$
Adding $(i+1) a_{i} a_{i-1}$ to both sides of the last inequality and multiplying both sides of the resulting inequality by $x y$ gives
$$
i \cdot 2 x y \cdot a_{i} a_{i-1} \geqslant(i+1) \cdot x y \cdot\left(a_{i+1} a_{i-2}+a_{i} a_{i-1}\right) .
$$
Finally, adding up (7), (8) and (9) results in
$$
i \cdot\left(x a_{i}+y a_{i-1}\right)^{2}>(i+1) \cdot\left(x a_{i+1}+y a_{i}\right)\left(x a_{i-1}+y a_{i-2}\right)
$$
which is equivalent to the claim.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\n15."
}
|
8821ba00-445e-59d8-9bdf-cd467ce57e3a
| 240,247
|
Let $f$ be a real-valued function defined on the positive integers satisfying the following condition: For all $n>1$ there exists a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Given that $f(2001)=1$, what is the value of $f(2002)$ ?
|
Answer: 2.
For any prime $p$ we have $f(p)=f(1)-f(p)$ and thus $f(p)=\frac{f(1)}{2}$. If $n$ is a product of two primes $p$ and $q$, then $f(n)=f(p)-f(q)$ or $f(n)=f(q)-f(p)$, so $f(n)=0$. By the same reasoning we find that if $n$ is a product of three primes, then there is a prime $p$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=-f(p)=-\frac{f(1)}{2} .
$$
By simple induction we can show that if $n$ is the product of $k$ primes, then $f(n)=(2-k) \cdot \frac{f(1)}{2}$. In particular, $f(2001)=f(3 \cdot 23 \cdot 29)=1$ so $f(1)=-2$. Therefore, $f(2002)=f(2 \cdot 7 \cdot 11 \cdot 13)=-f(1)=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f$ be a real-valued function defined on the positive integers satisfying the following condition: For all $n>1$ there exists a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Given that $f(2001)=1$, what is the value of $f(2002)$ ?
|
Answer: 2.
For any prime $p$ we have $f(p)=f(1)-f(p)$ and thus $f(p)=\frac{f(1)}{2}$. If $n$ is a product of two primes $p$ and $q$, then $f(n)=f(p)-f(q)$ or $f(n)=f(q)-f(p)$, so $f(n)=0$. By the same reasoning we find that if $n$ is a product of three primes, then there is a prime $p$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)=-f(p)=-\frac{f(1)}{2} .
$$
By simple induction we can show that if $n$ is the product of $k$ primes, then $f(n)=(2-k) \cdot \frac{f(1)}{2}$. In particular, $f(2001)=f(3 \cdot 23 \cdot 29)=1$ so $f(1)=-2$. Therefore, $f(2002)=f(2 \cdot 7 \cdot 11 \cdot 13)=-f(1)=2$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\n16."
}
|
63249da3-fd82-594e-b5b4-726b15645a5c
| 605,042
|
Let $n$ be a positive integer. Prove that at least $2^{n-1}+n$ numbers can be chosen from the set $\left\{1,2,3, \ldots, 2^{n}\right\}$ such that for any two different chosen numbers $x$ and $y, x+y$ is not a divisor of $x \cdot y$.
|
We choose the numbers $1,3,5, \ldots, 2^{n}-1$ and $2,4,8,16, \ldots, 2^{n}$, i.e. all odd numbers and all powers of 2 . Consider the three possible cases.
(1) If $x=2 a-1$ and $y=2 b-1$, then $x+y=(2 a-1)+(2 b-1)=2(a+b-1)$ is even and does not divide $x y=(2 a-1)(2 b-1)$ which is odd.
(2) If $x=2^{k}$ and $y=2^{m}$ where $k<m$, then $x+y=2^{k}\left(2^{m-k}+1\right)$ has an odd divisor greater than 1 and hence does not divide $x y=2^{a+b}$.
(3) If $x=2^{k}$ and $y=2 b-1$, then $x+y=2^{k}+(2 b-1)>(2 b-1)$ is odd and hence does not divide $x y=2^{k}(2 b-1)$ which has $2 b-1$ as its largest odd divisor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Prove that at least $2^{n-1}+n$ numbers can be chosen from the set $\left\{1,2,3, \ldots, 2^{n}\right\}$ such that for any two different chosen numbers $x$ and $y, x+y$ is not a divisor of $x \cdot y$.
|
We choose the numbers $1,3,5, \ldots, 2^{n}-1$ and $2,4,8,16, \ldots, 2^{n}$, i.e. all odd numbers and all powers of 2 . Consider the three possible cases.
(1) If $x=2 a-1$ and $y=2 b-1$, then $x+y=(2 a-1)+(2 b-1)=2(a+b-1)$ is even and does not divide $x y=(2 a-1)(2 b-1)$ which is odd.
(2) If $x=2^{k}$ and $y=2^{m}$ where $k<m$, then $x+y=2^{k}\left(2^{m-k}+1\right)$ has an odd divisor greater than 1 and hence does not divide $x y=2^{a+b}$.
(3) If $x=2^{k}$ and $y=2 b-1$, then $x+y=2^{k}+(2 b-1)>(2 b-1)$ is odd and hence does not divide $x y=2^{k}(2 b-1)$ which has $2 b-1$ as its largest odd divisor.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\n17."
}
|
1eacab8c-c907-5293-9147-6f6e3a31c519
| 240,265
|
Let $a$ be an odd integer. Prove that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ are relatively prime for all positive integers $n$ and $m$ with $n \neq m$.
|
Rewriting $a^{2^{n}}+2^{2^{n}}=a^{2^{n}}-2^{2^{n}}+2 \cdot 2^{2^{n}}$ and making repeated use of the identity
$$
a^{2^{n}}-2^{2^{n}}=\left(a^{2^{n-1}}-2^{2^{n-1}}\right) \cdot\left(a^{2^{n-1}}+2^{2^{n-1}}\right)
$$
we get
$$
\begin{gathered}
a^{2^{n}}+2^{2^{n}}=\left(a^{2^{n-1}}+2^{2^{n-1}}\right) \cdot\left(a^{2^{n-2}}+2^{2^{n-2}}\right) \cdot \ldots \cdot\left(a^{2^{m}}+2^{2^{m}}\right) \cdot \ldots \\
\ldots \cdot\left(a^{2}+2^{2}\right) \cdot(a+2) \cdot(a-2)+2 \cdot 2^{2^{n}}
\end{gathered}
$$
For $n>m$, assume that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ have a common divisor $d>1$. Then an odd integer $d$ divides $2 \cdot 2^{2^{n}}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ be an odd integer. Prove that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ are relatively prime for all positive integers $n$ and $m$ with $n \neq m$.
|
Rewriting $a^{2^{n}}+2^{2^{n}}=a^{2^{n}}-2^{2^{n}}+2 \cdot 2^{2^{n}}$ and making repeated use of the identity
$$
a^{2^{n}}-2^{2^{n}}=\left(a^{2^{n-1}}-2^{2^{n-1}}\right) \cdot\left(a^{2^{n-1}}+2^{2^{n-1}}\right)
$$
we get
$$
\begin{gathered}
a^{2^{n}}+2^{2^{n}}=\left(a^{2^{n-1}}+2^{2^{n-1}}\right) \cdot\left(a^{2^{n-2}}+2^{2^{n-2}}\right) \cdot \ldots \cdot\left(a^{2^{m}}+2^{2^{m}}\right) \cdot \ldots \\
\ldots \cdot\left(a^{2}+2^{2}\right) \cdot(a+2) \cdot(a-2)+2 \cdot 2^{2^{n}}
\end{gathered}
$$
For $n>m$, assume that $a^{2^{n}}+2^{2^{n}}$ and $a^{2^{m}}+2^{2^{m}}$ have a common divisor $d>1$. Then an odd integer $d$ divides $2 \cdot 2^{2^{n}}$, a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\n18."
}
|
a8e01fa4-2c0b-513a-afec-18d1951e6e13
| 240,276
|
What is the smallest positive odd integer having the same number of positive divisors as 360 ?
|
Answer: 31185 .
An integer with the prime factorization $p_{1}^{r_{1}} \cdot p_{2}^{r_{2}} \cdot \ldots \cdot p_{k}^{r_{k}}$ (where $p_{1}, p_{2}, \ldots$, $p_{k}$ are distinct primes) has precisely $\left(r_{1}+1\right) \cdot\left(r_{2}+1\right) \cdot \ldots \cdot\left(r_{k}+1\right)$ distinct positive divisors. Since $360=2^{3} \cdot 3^{2} \cdot 5$, it follows that 360 has $4 \cdot 3 \cdot 2=24$ positive divisors. Since $24=3 \cdot 2 \cdot 2 \cdot 2$, it is easy to check that the smallest odd number with 24 positive divisors is $3^{2} \cdot 5 \cdot 7 \cdot 11=31185$.
|
31185
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the smallest positive odd integer having the same number of positive divisors as 360 ?
|
Answer: 31185 .
An integer with the prime factorization $p_{1}^{r_{1}} \cdot p_{2}^{r_{2}} \cdot \ldots \cdot p_{k}^{r_{k}}$ (where $p_{1}, p_{2}, \ldots$, $p_{k}$ are distinct primes) has precisely $\left(r_{1}+1\right) \cdot\left(r_{2}+1\right) \cdot \ldots \cdot\left(r_{k}+1\right)$ distinct positive divisors. Since $360=2^{3} \cdot 3^{2} \cdot 5$, it follows that 360 has $4 \cdot 3 \cdot 2=24$ positive divisors. Since $24=3 \cdot 2 \cdot 2 \cdot 2$, it is easy to check that the smallest odd number with 24 positive divisors is $3^{2} \cdot 5 \cdot 7 \cdot 11=31185$.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\n19."
}
|
cc624072-0d9c-5339-981c-b2708ba14fe4
| 605,096
|
From a sequence of integers $(a, b, c, d)$ each of the sequences
$$
(c, d, a, b),(b, a, d, c),(a+n c, b+n d, c, d),(a+n b, b, c+n d, d),
$$
for arbitrary integer $n$ can be obtained by one step. Is it possible to obtain $(3,4,5,7)$ from $(1,2,3,4)$ through a sequence of such steps?
## Solutions
|
Answer: no.
Under all transformations $(a, b, c, d) \rightarrow\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)$ allowed in the problem we have $|a d-b c|=\left|a^{\prime} d^{\prime}-b^{\prime} c^{\prime}\right|$, but $|1 \cdot 4-2 \cdot 3|=2 \neq 1=|3 \cdot 7-4 \cdot 5|$.
Remark. The transformations allowed in the problem are in fact the elementary transformations of the determinant
$$
\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|
$$
and the invariant $|a d-b c|$ is the absolute value of the determinant which is preserved under these transformations.
|
no
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
From a sequence of integers $(a, b, c, d)$ each of the sequences
$$
(c, d, a, b),(b, a, d, c),(a+n c, b+n d, c, d),(a+n b, b, c+n d, d),
$$
for arbitrary integer $n$ can be obtained by one step. Is it possible to obtain $(3,4,5,7)$ from $(1,2,3,4)$ through a sequence of such steps?
## Solutions
|
Answer: no.
Under all transformations $(a, b, c, d) \rightarrow\left(a^{\prime}, b^{\prime}, c^{\prime}, d^{\prime}\right)$ allowed in the problem we have $|a d-b c|=\left|a^{\prime} d^{\prime}-b^{\prime} c^{\prime}\right|$, but $|1 \cdot 4-2 \cdot 3|=2 \neq 1=|3 \cdot 7-4 \cdot 5|$.
Remark. The transformations allowed in the problem are in fact the elementary transformations of the determinant
$$
\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|
$$
and the invariant $|a d-b c|$ is the absolute value of the determinant which is preserved under these transformations.
|
{
"resource_path": "BalticWay/segmented/en-bw01sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\n20."
}
|
a2242792-7cf1-5504-b5cb-07723d91ae8b
| 605,107
|
Solve the system of equations
$$
\left\{\begin{array}{l}
a^{3}+3 a b^{2}+3 a c^{2}-6 a b c=1 \\
b^{3}+3 b a^{2}+3 b c^{2}-6 a b c=1 \\
c^{3}+3 c a^{2}+3 c b^{2}-6 a b c=1
\end{array}\right.
$$
in real numbers.
Answer: $a=1, b=1, c=1$.
|
Denoting the left hand sides of the given equations as $A, B$ and $C$, the following equalities can easily be seen to hold:
$$
\begin{aligned}
-A+B+C & =(-a+b+c)^{3} \\
A-B+C & =(a-b+c)^{3} \\
A+B-C & =(a+b-c)^{3} .
\end{aligned}
$$
Hence, the system of equations given in the problem is equivalent to the following one:
$$
\left\{\begin{array}{c}
(-a+b+c)^{3}=1 \\
(a-b+c)^{3}=1 \\
(a+b-c)^{3}=1
\end{array}\right.
$$
which gives
$$
\left\{\begin{array}{c}
-a+b+c=1 \\
a-b+c=1 \\
a+b-c=1
\end{array} .\right.
$$
The unique solution of this system is $(a, b, c)=(1,1,1)$.
|
(a, b, c)=(1,1,1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Solve the system of equations
$$
\left\{\begin{array}{l}
a^{3}+3 a b^{2}+3 a c^{2}-6 a b c=1 \\
b^{3}+3 b a^{2}+3 b c^{2}-6 a b c=1 \\
c^{3}+3 c a^{2}+3 c b^{2}-6 a b c=1
\end{array}\right.
$$
in real numbers.
Answer: $a=1, b=1, c=1$.
|
Denoting the left hand sides of the given equations as $A, B$ and $C$, the following equalities can easily be seen to hold:
$$
\begin{aligned}
-A+B+C & =(-a+b+c)^{3} \\
A-B+C & =(a-b+c)^{3} \\
A+B-C & =(a+b-c)^{3} .
\end{aligned}
$$
Hence, the system of equations given in the problem is equivalent to the following one:
$$
\left\{\begin{array}{c}
(-a+b+c)^{3}=1 \\
(a-b+c)^{3}=1 \\
(a+b-c)^{3}=1
\end{array}\right.
$$
which gives
$$
\left\{\begin{array}{c}
-a+b+c=1 \\
a-b+c=1 \\
a+b-c=1
\end{array} .\right.
$$
The unique solution of this system is $(a, b, c)=(1,1,1)$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution."
}
|
659419e1-87d2-5b11-8ef1-d8a4b9debe47
| 236,512
|
Let $a, b, c, d$ be real numbers such that
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0
\end{aligned}
$$
Prove that at least one of the numbers $a, b, c, d$ is not greater than -1 .
|
We can assume that $a$ is the least among $a, b, c, d$ (or one of the least, if some of them are equal), there are $n>0$ negative numbers among $a, b, c, d$, and the sum of the positive ones is $x$.
Then we obtain
$$
-2=a+b+c+d \geqslant n a+x .
$$
Squaring we get
$$
4=a^{2}+b^{2}+c^{2}+d^{2}
$$
which implies
$$
4 \leqslant n \cdot a^{2}+x^{2}
$$
as the square of the sum of positive numbers is not less than the sum of their squares.
Combining inequalities (1) and (2) we obtain
$$
\begin{aligned}
n a^{2}+(n a+2)^{2} & \geqslant 4, \\
n a^{2}+n^{2} a^{2}+4 n a & \geqslant 0, \\
a^{2}+n a^{2}+4 a & \geqslant 0 .
\end{aligned}
$$
As $n \leqslant 3$ (if all the numbers are negative, the second condition of the problem cannot be satisfied), we obtain from the last inequality that
$$
\begin{aligned}
& 4 a^{2}+4 a \geqslant 0, \\
& a(a+1) \geqslant 0 .
\end{aligned}
$$
As $a<0$ it follows that $a \leqslant-1$.
Alternative solution. Assume that $a, b, c, d>-1$. Denoting $A=a+1, B=b+1, C=c+1, D=d+1$ we have $A, B, C, D>0$. Then the first equation gives
$$
A+B+C+D=2 \text {. }
$$
We also have
$$
a b=(A-1)(B-1)=A B-A-B+1 .
$$
Adding 5 similar terms to the last one we get from the second equation
$$
A B+A C+A D+B C+B D+C D-3(A+B+C+D)+6=0 .
$$
In view of (3) this implies
$$
A B+A C+A D+B C+B D+C D=0,
$$
a contradiction as all the unknowns $A, B, C, D$ were supposed to be positive.
Another solution. Assume that the conditions of the problem hold:
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0 .
\end{aligned}
$$
Suppose that
$$
a, b, c, d>-1 \text {. }
$$
If all of $a, b, c, d$ were negative, then (5) could not be satisfied, so at most three of them are negative. If two or less of them were negative, then (6) would imply that the sum of negative numbers, and hence also the sum $a+b+c+d$, is greater than $2 \cdot(-1)=-2$, which contradicts (4). So exactly three of $a, b, c, d$ are negative and one is nonnegative. Let $d$ be the nonnegative one. Then $d=-2-(a+b+c)<-2-(-1-1-1)=1$. Obviously $|a|,|b|,|c|,|d|<1$. Squaring (4) and subtracting 2 times (5), we get
$$
a^{2}+b^{2}+c^{2}+d^{2}=4,
$$
but
$$
a^{2}+b^{2}+c^{2}+d^{2}=|a|^{2}+|b|^{2}+|c|^{2}+|d|^{2}<4,
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b, c, d$ be real numbers such that
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0
\end{aligned}
$$
Prove that at least one of the numbers $a, b, c, d$ is not greater than -1 .
|
We can assume that $a$ is the least among $a, b, c, d$ (or one of the least, if some of them are equal), there are $n>0$ negative numbers among $a, b, c, d$, and the sum of the positive ones is $x$.
Then we obtain
$$
-2=a+b+c+d \geqslant n a+x .
$$
Squaring we get
$$
4=a^{2}+b^{2}+c^{2}+d^{2}
$$
which implies
$$
4 \leqslant n \cdot a^{2}+x^{2}
$$
as the square of the sum of positive numbers is not less than the sum of their squares.
Combining inequalities (1) and (2) we obtain
$$
\begin{aligned}
n a^{2}+(n a+2)^{2} & \geqslant 4, \\
n a^{2}+n^{2} a^{2}+4 n a & \geqslant 0, \\
a^{2}+n a^{2}+4 a & \geqslant 0 .
\end{aligned}
$$
As $n \leqslant 3$ (if all the numbers are negative, the second condition of the problem cannot be satisfied), we obtain from the last inequality that
$$
\begin{aligned}
& 4 a^{2}+4 a \geqslant 0, \\
& a(a+1) \geqslant 0 .
\end{aligned}
$$
As $a<0$ it follows that $a \leqslant-1$.
Alternative solution. Assume that $a, b, c, d>-1$. Denoting $A=a+1, B=b+1, C=c+1, D=d+1$ we have $A, B, C, D>0$. Then the first equation gives
$$
A+B+C+D=2 \text {. }
$$
We also have
$$
a b=(A-1)(B-1)=A B-A-B+1 .
$$
Adding 5 similar terms to the last one we get from the second equation
$$
A B+A C+A D+B C+B D+C D-3(A+B+C+D)+6=0 .
$$
In view of (3) this implies
$$
A B+A C+A D+B C+B D+C D=0,
$$
a contradiction as all the unknowns $A, B, C, D$ were supposed to be positive.
Another solution. Assume that the conditions of the problem hold:
$$
\begin{aligned}
a+b+c+d & =-2 \\
a b+a c+a d+b c+b d+c d & =0 .
\end{aligned}
$$
Suppose that
$$
a, b, c, d>-1 \text {. }
$$
If all of $a, b, c, d$ were negative, then (5) could not be satisfied, so at most three of them are negative. If two or less of them were negative, then (6) would imply that the sum of negative numbers, and hence also the sum $a+b+c+d$, is greater than $2 \cdot(-1)=-2$, which contradicts (4). So exactly three of $a, b, c, d$ are negative and one is nonnegative. Let $d$ be the nonnegative one. Then $d=-2-(a+b+c)<-2-(-1-1-1)=1$. Obviously $|a|,|b|,|c|,|d|<1$. Squaring (4) and subtracting 2 times (5), we get
$$
a^{2}+b^{2}+c^{2}+d^{2}=4,
$$
but
$$
a^{2}+b^{2}+c^{2}+d^{2}=|a|^{2}+|b|^{2}+|c|^{2}+|d|^{2}<4,
$$
a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
60afcc44-95be-55cc-9a7b-22489ab96619
| 605,136
|
Find all sequences $a_{0} \leqslant a_{1} \leqslant a_{2} \leqslant \ldots$ of real numbers such that
$$
a_{m^{2}+n^{2}}=a_{m}^{2}+a_{n}^{2}
$$
for all integers $m, n \geqslant 0$.
Answer: $a_{n} \equiv 0, a_{n} \equiv \frac{1}{2}$ and $a_{n}=n$.
|
Denoting $f(n)=a_{n}$ we have
$$
f\left(m^{2}+n^{2}\right)=f^{2}(m)+f^{2}(n) .
$$
Substituting $m=n=0$ into (7) we get $f(0)=2 f^{2}(0)$, hence either $f(0)=\frac{1}{2}$ or $f(0)=0$. We consider these cases separately.
(1) If $f(0)=\frac{1}{2}$ then substituting $m=1$ and $n=0$ into (7) we obtain $f(1)=f^{2}(1)+\frac{1}{4}$, whence $\left(f(1)-\frac{1}{2}\right)^{2}=0$ and $f(1)=\frac{1}{2}$. Now,
$$
\begin{aligned}
& f(2)=f\left(1^{2}+1^{2}\right)=2 f^{2}(1)=\frac{1}{2}, \\
& f(8)=f\left(2^{2}+2^{2}\right)=2 f^{2}(2)=\frac{1}{2},
\end{aligned}
$$
etc, implying that $f\left(2^{i}\right)=\frac{1}{2}$ for arbitrarily large natural $i$ and, due to monotonity, $f(n)=\frac{1}{2}$ for every natural $n$.
(2) If $f(0)=0$ then by substituting $m=1, n=0$ into (7) we obtain $f(1)=f^{2}(1)$ and hence, $f(1)=0$ or $f(1)=1$. This gives two subcases.
(2a) If $f(0)=0$ and $f(1)=0$ then by the same technique as above we see that $f\left(2^{i}\right)=0$ for arbitrarily large natural $i$ and, due to monotonity, $f(n)=0$ for every natural $n$.
(2b) If $f(0)=0$ and $f(1)=1$ then we compute
$$
\begin{aligned}
& f(2)=f\left(1^{2}+1^{2}\right)=2 f^{2}(1)=2, \\
& f(4)=f\left(2^{2}+0^{2}\right)=f^{2}(2)=4, \\
& f(5)=f\left(2^{2}+1^{2}\right)=f^{2}(2)+f^{2}(1)=5 .
\end{aligned}
$$
Now,
$$
f^{2}(3)+f^{2}(4)=f(25)=f^{2}(5)+f^{2}(0)=25,
$$
hence $f^{2}(3)=25-16=9$ and $f(3)=3$. Further,
$$
\begin{aligned}
f(8) & =f\left(2^{2}+2^{2}\right)=2 f^{2}(2)=8 \\
f(9) & =f\left(3^{2}+0^{2}\right)=f^{2}(3)=9 \\
f(10) & =f\left(3^{2}+1^{2}\right)=f^{2}(3)+f^{2}(1)=10
\end{aligned}
$$
From the equalities
$$
\begin{aligned}
& f^{2}(6)+f^{2}(8)=f^{2}(10)+f^{2}(0), \\
& f^{2}(7)+f^{2}(1)=f^{2}(5)+f^{2}(5)
\end{aligned}
$$
we also conclude that $f(6)=6$ and $f(7)=7$. It remains to note that
$$
\begin{aligned}
& (2 k+1)^{2}+(k-2)^{2}=(2 k-1)^{2}+(k+2)^{2}, \\
& (2 k+2)^{2}+(k-4)^{2}=(2 k-2)^{2}+(k+4)^{2}
\end{aligned}
$$
and by induction it follows that $f(n)=n$ for every natural $n$.
|
a_{n} \equiv 0, a_{n} \equiv \frac{1}{2}, a_{n}=n
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all sequences $a_{0} \leqslant a_{1} \leqslant a_{2} \leqslant \ldots$ of real numbers such that
$$
a_{m^{2}+n^{2}}=a_{m}^{2}+a_{n}^{2}
$$
for all integers $m, n \geqslant 0$.
Answer: $a_{n} \equiv 0, a_{n} \equiv \frac{1}{2}$ and $a_{n}=n$.
|
Denoting $f(n)=a_{n}$ we have
$$
f\left(m^{2}+n^{2}\right)=f^{2}(m)+f^{2}(n) .
$$
Substituting $m=n=0$ into (7) we get $f(0)=2 f^{2}(0)$, hence either $f(0)=\frac{1}{2}$ or $f(0)=0$. We consider these cases separately.
(1) If $f(0)=\frac{1}{2}$ then substituting $m=1$ and $n=0$ into (7) we obtain $f(1)=f^{2}(1)+\frac{1}{4}$, whence $\left(f(1)-\frac{1}{2}\right)^{2}=0$ and $f(1)=\frac{1}{2}$. Now,
$$
\begin{aligned}
& f(2)=f\left(1^{2}+1^{2}\right)=2 f^{2}(1)=\frac{1}{2}, \\
& f(8)=f\left(2^{2}+2^{2}\right)=2 f^{2}(2)=\frac{1}{2},
\end{aligned}
$$
etc, implying that $f\left(2^{i}\right)=\frac{1}{2}$ for arbitrarily large natural $i$ and, due to monotonity, $f(n)=\frac{1}{2}$ for every natural $n$.
(2) If $f(0)=0$ then by substituting $m=1, n=0$ into (7) we obtain $f(1)=f^{2}(1)$ and hence, $f(1)=0$ or $f(1)=1$. This gives two subcases.
(2a) If $f(0)=0$ and $f(1)=0$ then by the same technique as above we see that $f\left(2^{i}\right)=0$ for arbitrarily large natural $i$ and, due to monotonity, $f(n)=0$ for every natural $n$.
(2b) If $f(0)=0$ and $f(1)=1$ then we compute
$$
\begin{aligned}
& f(2)=f\left(1^{2}+1^{2}\right)=2 f^{2}(1)=2, \\
& f(4)=f\left(2^{2}+0^{2}\right)=f^{2}(2)=4, \\
& f(5)=f\left(2^{2}+1^{2}\right)=f^{2}(2)+f^{2}(1)=5 .
\end{aligned}
$$
Now,
$$
f^{2}(3)+f^{2}(4)=f(25)=f^{2}(5)+f^{2}(0)=25,
$$
hence $f^{2}(3)=25-16=9$ and $f(3)=3$. Further,
$$
\begin{aligned}
f(8) & =f\left(2^{2}+2^{2}\right)=2 f^{2}(2)=8 \\
f(9) & =f\left(3^{2}+0^{2}\right)=f^{2}(3)=9 \\
f(10) & =f\left(3^{2}+1^{2}\right)=f^{2}(3)+f^{2}(1)=10
\end{aligned}
$$
From the equalities
$$
\begin{aligned}
& f^{2}(6)+f^{2}(8)=f^{2}(10)+f^{2}(0), \\
& f^{2}(7)+f^{2}(1)=f^{2}(5)+f^{2}(5)
\end{aligned}
$$
we also conclude that $f(6)=6$ and $f(7)=7$. It remains to note that
$$
\begin{aligned}
& (2 k+1)^{2}+(k-2)^{2}=(2 k-1)^{2}+(k+2)^{2}, \\
& (2 k+2)^{2}+(k-4)^{2}=(2 k-2)^{2}+(k+4)^{2}
\end{aligned}
$$
and by induction it follows that $f(n)=n$ for every natural $n$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
71c3cfe3-3394-5c9a-ad46-61804725a44f
| 236,533
|
Let $n$ be a positive integer. Prove that
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
for all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{n}$ such that $x_{1}+x_{2}+\cdots+x_{n}=1$.
|
Expanding the expressions at both sides we obtain the equivalent inequality
$$
-\sum_{i} x_{i}^{3}+2 \sum_{i} x_{i}^{2}-\frac{2}{n}+\frac{1}{n^{2}} \geqslant 0
$$
It is easy to check that the left hand side is equal to
$$
\sum_{i}\left(2-\frac{2}{n}-x_{i}\right)\left(x_{i}-\frac{1}{n}\right)^{2}
$$
and hence is nonnegative.
Alternative solution. First note that for $n=1$ the required condition holds trivially, and for $n=2$ we have
$$
x(1-x)^{2}+(1-x) x^{2}=x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}=\left(1-\frac{1}{2}\right)^{2} .
$$
So we may further consider the case $n \geqslant 3$.
Assume first that for each index $i$ the inequality $x_{i}<\frac{2}{3}$ holds. Let $f(x)=x(1-x)^{2}=x-2 x^{2}+x^{3}$, then $f^{\prime \prime}(x)=6 x-4$. Hence, the function $f$ is concave in the interval $\left[0, \frac{2}{3}\right]$. Thus, from Jensen's inequality we have
$$
\begin{aligned}
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} & =\sum_{i=1}^{n} f\left(x_{i}\right) \leqslant n \cdot f\left(\frac{x_{1}+\ldots+x_{n}}{n}\right)=n \cdot f\left(\frac{1}{n}\right)= \\
& =n \cdot \frac{1}{n}\left(1-\frac{1}{n}\right)^{2}=\left(1-\frac{1}{n}\right)^{2} .
\end{aligned}
$$
If some $x_{i} \geqslant \frac{2}{3}$ then we have
$$
x_{i}\left(1-x_{i}\right)^{2} \leqslant 1 \cdot\left(1-\frac{2}{3}\right)^{2}=\frac{1}{9}
$$
For the rest of the terms we have
$$
\sum_{j \neq i} x_{j}\left(1-x_{j}\right)^{2} \leqslant \sum_{j \neq i} x_{j}=1-x_{i} \leqslant \frac{1}{3}
$$
Hence,
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant \frac{1}{9}+\frac{1}{3}=\frac{4}{9} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
as $n \geqslant 3$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer. Prove that
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
for all nonnegative real numbers $x_{1}, x_{2}, \ldots, x_{n}$ such that $x_{1}+x_{2}+\cdots+x_{n}=1$.
|
Expanding the expressions at both sides we obtain the equivalent inequality
$$
-\sum_{i} x_{i}^{3}+2 \sum_{i} x_{i}^{2}-\frac{2}{n}+\frac{1}{n^{2}} \geqslant 0
$$
It is easy to check that the left hand side is equal to
$$
\sum_{i}\left(2-\frac{2}{n}-x_{i}\right)\left(x_{i}-\frac{1}{n}\right)^{2}
$$
and hence is nonnegative.
Alternative solution. First note that for $n=1$ the required condition holds trivially, and for $n=2$ we have
$$
x(1-x)^{2}+(1-x) x^{2}=x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}=\left(1-\frac{1}{2}\right)^{2} .
$$
So we may further consider the case $n \geqslant 3$.
Assume first that for each index $i$ the inequality $x_{i}<\frac{2}{3}$ holds. Let $f(x)=x(1-x)^{2}=x-2 x^{2}+x^{3}$, then $f^{\prime \prime}(x)=6 x-4$. Hence, the function $f$ is concave in the interval $\left[0, \frac{2}{3}\right]$. Thus, from Jensen's inequality we have
$$
\begin{aligned}
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} & =\sum_{i=1}^{n} f\left(x_{i}\right) \leqslant n \cdot f\left(\frac{x_{1}+\ldots+x_{n}}{n}\right)=n \cdot f\left(\frac{1}{n}\right)= \\
& =n \cdot \frac{1}{n}\left(1-\frac{1}{n}\right)^{2}=\left(1-\frac{1}{n}\right)^{2} .
\end{aligned}
$$
If some $x_{i} \geqslant \frac{2}{3}$ then we have
$$
x_{i}\left(1-x_{i}\right)^{2} \leqslant 1 \cdot\left(1-\frac{2}{3}\right)^{2}=\frac{1}{9}
$$
For the rest of the terms we have
$$
\sum_{j \neq i} x_{j}\left(1-x_{j}\right)^{2} \leqslant \sum_{j \neq i} x_{j}=1-x_{i} \leqslant \frac{1}{3}
$$
Hence,
$$
\sum_{i=1}^{n} x_{i}\left(1-x_{i}\right)^{2} \leqslant \frac{1}{9}+\frac{1}{3}=\frac{4}{9} \leqslant\left(1-\frac{1}{n}\right)^{2}
$$
as $n \geqslant 3$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
7e81f685-983f-5182-b108-70c389480c17
| 605,166
|
Find all pairs $(a, b)$ of positive rational numbers such that
$$
\sqrt{a}+\sqrt{b}=\sqrt{2+\sqrt{3}} .
$$
Answer: $(a, b)=\left(\frac{1}{2}, \frac{3}{2}\right)$ or $(a, b)=\left(\frac{3}{2}, \frac{1}{2}\right)$.
|
Squaring both sides of the equation gives
$$
a+b+2 \sqrt{a b}=2+\sqrt{3}
$$
so $2 \sqrt{a b}=r+\sqrt{3}$ for some rational number $r$. Squaring both sides of this gives $4 a b=r^{2}+3+2 r \sqrt{3}$, so $2 r \sqrt{3}$ is rational, which implies $r=0$. Hence $a b=3 / 4$ and substituting this into (8) gives $a+b=2$. Solving for $a$ and $b$ gives $(a, b)=\left(\frac{1}{2}, \frac{3}{2}\right)$ or $(a, b)=\left(\frac{3}{2}, \frac{1}{2}\right)$.
|
(a, b)=\left(\frac{1}{2}, \frac{3}{2}\right) \text{ or } (a, b)=\left(\frac{3}{2}, \frac{1}{2}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all pairs $(a, b)$ of positive rational numbers such that
$$
\sqrt{a}+\sqrt{b}=\sqrt{2+\sqrt{3}} .
$$
Answer: $(a, b)=\left(\frac{1}{2}, \frac{3}{2}\right)$ or $(a, b)=\left(\frac{3}{2}, \frac{1}{2}\right)$.
|
Squaring both sides of the equation gives
$$
a+b+2 \sqrt{a b}=2+\sqrt{3}
$$
so $2 \sqrt{a b}=r+\sqrt{3}$ for some rational number $r$. Squaring both sides of this gives $4 a b=r^{2}+3+2 r \sqrt{3}$, so $2 r \sqrt{3}$ is rational, which implies $r=0$. Hence $a b=3 / 4$ and substituting this into (8) gives $a+b=2$. Solving for $a$ and $b$ gives $(a, b)=\left(\frac{1}{2}, \frac{3}{2}\right)$ or $(a, b)=\left(\frac{3}{2}, \frac{1}{2}\right)$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
bd8bb52f-a224-5e01-8b47-bf6022fb4dd2
| 236,558
|
The following solitaire game is played on an $m \times n$ rectangular board, $m, n \geqslant 2$, divided into unit squares. First, a rook is placed on some square. At each move, the rook can be moved an arbitrary number of squares horizontally or vertically, with the extra condition that each move has to be made in the $90^{\circ}$ clockwise direction compared to the previous one (e.g. after a move to the left, the next one has to be done upwards, the next one to the right etc). For which values of $m$ and $n$ is it possible that the rook visits every square of the board exactly once and returns to the first square? (The rook is considered to visit only those squares it stops on, and not the ones it steps over.)
Answer: $m, n \equiv 0 \bmod 2$.
|
First, consider any row that is not the row where the rook starts from. The rook has to visit all the squares of that row exactly once, and on its tour around the board, every time it visits this row, exactly two squares get visited. Hence, $m$ must be even; a similar argument for the columns shows that $n$ must also be even.
It remains to prove that for any even $m$ and $n$ such a tour is possible. We will show it by an inductionlike argument. Labelling the squares with pairs of integers $(i, j)$, where $1 \leqslant i \leqslant m$ and $1 \leqslant j \leqslant n$, we start moving from the square $(m / 2+1,1)$ and first cover all the squares of the top and bottom rows in the order shown in the figure below, except for the squares $(m / 2-1, n)$ and $(m / 2+1, n)$; note that we finish on the square $(m / 2-1,1)$.
The next square to visit will be $(m / 2-1, n-1)$ and now we will cover the rows numbered 2 and $n-1$, except for the two middle squares in row 2 . Continuing in this way we can visit all the squares except for the two middle squares in every second row (note that here we need the assumption that $m$ and $n$ are even):
| 3 | 7 | | | 8 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 15 | 19 | 11 | 20 | 16 | 12 |
| 23 | 27 | | | 28 | 24 |
| 35 | 39 | 31 | 40 | 36 | 32 |
| 34 | 38 | | | 37 | 33 |
| 22 | 26 | 30 | 21 | 29 | 25 |
| 14 | 18 | | | 17 | 13 |
| 2 | 6 | 10 | 1 | 9 | 5 |
The rest of the squares can be visited easily:
| 3 | 7 | 47 | 48 | 8 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 15 | 19 | 11 | 20 | 16 | 12 |
| 23 | 27 | 43 | 44 | 28 | 24 |
| 35 | 39 | 31 | 40 | 36 | 32 |
| 34 | 38 | 42 | 41 | 37 | 33 |
| 22 | 26 | 30 | 21 | 29 | 25 |
| 14 | 18 | 46 | 45 | 17 | 13 |
| 2 | 6 | 10 | 1 | 9 | 5 |
|
m, n \equiv 0 \bmod 2
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The following solitaire game is played on an $m \times n$ rectangular board, $m, n \geqslant 2$, divided into unit squares. First, a rook is placed on some square. At each move, the rook can be moved an arbitrary number of squares horizontally or vertically, with the extra condition that each move has to be made in the $90^{\circ}$ clockwise direction compared to the previous one (e.g. after a move to the left, the next one has to be done upwards, the next one to the right etc). For which values of $m$ and $n$ is it possible that the rook visits every square of the board exactly once and returns to the first square? (The rook is considered to visit only those squares it stops on, and not the ones it steps over.)
Answer: $m, n \equiv 0 \bmod 2$.
|
First, consider any row that is not the row where the rook starts from. The rook has to visit all the squares of that row exactly once, and on its tour around the board, every time it visits this row, exactly two squares get visited. Hence, $m$ must be even; a similar argument for the columns shows that $n$ must also be even.
It remains to prove that for any even $m$ and $n$ such a tour is possible. We will show it by an inductionlike argument. Labelling the squares with pairs of integers $(i, j)$, where $1 \leqslant i \leqslant m$ and $1 \leqslant j \leqslant n$, we start moving from the square $(m / 2+1,1)$ and first cover all the squares of the top and bottom rows in the order shown in the figure below, except for the squares $(m / 2-1, n)$ and $(m / 2+1, n)$; note that we finish on the square $(m / 2-1,1)$.

The next square to visit will be $(m / 2-1, n-1)$ and now we will cover the rows numbered 2 and $n-1$, except for the two middle squares in row 2 . Continuing in this way we can visit all the squares except for the two middle squares in every second row (note that here we need the assumption that $m$ and $n$ are even):
| 3 | 7 | | | 8 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 15 | 19 | 11 | 20 | 16 | 12 |
| 23 | 27 | | | 28 | 24 |
| 35 | 39 | 31 | 40 | 36 | 32 |
| 34 | 38 | | | 37 | 33 |
| 22 | 26 | 30 | 21 | 29 | 25 |
| 14 | 18 | | | 17 | 13 |
| 2 | 6 | 10 | 1 | 9 | 5 |
The rest of the squares can be visited easily:
| 3 | 7 | 47 | 48 | 8 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 15 | 19 | 11 | 20 | 16 | 12 |
| 23 | 27 | 43 | 44 | 28 | 24 |
| 35 | 39 | 31 | 40 | 36 | 32 |
| 34 | 38 | 42 | 41 | 37 | 33 |
| 22 | 26 | 30 | 21 | 29 | 25 |
| 14 | 18 | 46 | 45 | 17 | 13 |
| 2 | 6 | 10 | 1 | 9 | 5 |
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution."
}
|
d13a02f7-2a0a-528b-8731-69a058eba43f
| 236,568
|
We draw $n$ convex quadrilaterals in the plane. They divide the plane into regions (one of the regions is infinite). Determine the maximal possible number of these regions.
Answer: The maximal number of regions is $4 n^{2}-4 n+2$.
|
One quadrilateral produces two regions. Suppose we have drawn $k$ quadrilaterals $Q_{1}, \ldots, Q_{k}$ and produced $a_{k}$ regions. We draw another quadrilateral $Q_{k+1}$ and try to evaluate the number of regions $a_{k+1}$ now produced. Our task is to make $a_{k+1}$ as large as possible. Note that in a maximal configuration, no vertex of any $Q_{i}$ can be located on the edge of another quadrilateral as otherwise we could move this vertex a little bit to produce an extra region.
Because of this fact and the convexity of the $Q_{j}$ 's, any one of the four sides of $Q_{k+1}$ meets at most two sides of any $Q_{j}$. So the sides of $Q_{k+1}$ are divided into at most $2 k+1$ segments, each of which potentially grows the number of regions by one (being part of the common boundary of two parts, one of which is counted in $a_{k}$ ).
But if a side of $Q_{k+1}$ intersects the boundary of each $Q_{j}, 1 \leqslant j \leqslant k$ twice, then its endpoints (vertices of $Q_{k+1}$ ) are in the region outside of all the $Q_{j}$-s, and the the segments meeting at such a vertex are on the boundary of a single new part (recall that it makes no sense to put vertices on edges of another quadrilaterals). This means that $a_{k+1}-a_{k} \leqslant 4(2 k+1)-4=8 k$. By considering squares inscribed in a circle one easily sees that the situation where $a_{k+1}-a_{k}=8 k$ can be reached.
It remains to determine the expression for the maximal $a_{k}$. Since the difference $a_{k+1}-a_{k}$ is linear in $k, a_{k}$ is a quadratic polynomial in $k$, and $a_{0}=2$. So $a_{k}=A k^{2}+B k+2$. We have $8 k=a_{k+1}-a_{k}=A(2 k+1)+B$ for all $k$. This implies $A=4, B=-4$, and $a_{n}=4 n^{2}-4 n+2$.
|
4 n^{2}-4 n+2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
We draw $n$ convex quadrilaterals in the plane. They divide the plane into regions (one of the regions is infinite). Determine the maximal possible number of these regions.
Answer: The maximal number of regions is $4 n^{2}-4 n+2$.
|
One quadrilateral produces two regions. Suppose we have drawn $k$ quadrilaterals $Q_{1}, \ldots, Q_{k}$ and produced $a_{k}$ regions. We draw another quadrilateral $Q_{k+1}$ and try to evaluate the number of regions $a_{k+1}$ now produced. Our task is to make $a_{k+1}$ as large as possible. Note that in a maximal configuration, no vertex of any $Q_{i}$ can be located on the edge of another quadrilateral as otherwise we could move this vertex a little bit to produce an extra region.
Because of this fact and the convexity of the $Q_{j}$ 's, any one of the four sides of $Q_{k+1}$ meets at most two sides of any $Q_{j}$. So the sides of $Q_{k+1}$ are divided into at most $2 k+1$ segments, each of which potentially grows the number of regions by one (being part of the common boundary of two parts, one of which is counted in $a_{k}$ ).
But if a side of $Q_{k+1}$ intersects the boundary of each $Q_{j}, 1 \leqslant j \leqslant k$ twice, then its endpoints (vertices of $Q_{k+1}$ ) are in the region outside of all the $Q_{j}$-s, and the the segments meeting at such a vertex are on the boundary of a single new part (recall that it makes no sense to put vertices on edges of another quadrilaterals). This means that $a_{k+1}-a_{k} \leqslant 4(2 k+1)-4=8 k$. By considering squares inscribed in a circle one easily sees that the situation where $a_{k+1}-a_{k}=8 k$ can be reached.
It remains to determine the expression for the maximal $a_{k}$. Since the difference $a_{k+1}-a_{k}$ is linear in $k, a_{k}$ is a quadratic polynomial in $k$, and $a_{0}=2$. So $a_{k}=A k^{2}+B k+2$. We have $8 k=a_{k+1}-a_{k}=A(2 k+1)+B$ for all $k$. This implies $A=4, B=-4$, and $a_{n}=4 n^{2}-4 n+2$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\nSolution."
}
|
2ebe0de7-73b1-5fb7-bb21-3407b0efef7f
| 236,576
|
Let $P$ be a set of $n \geqslant 3$ points in the plane, no three of which are on a line. How many possibilities are there to choose a set $T$ of $\left(\begin{array}{c}n-1 \\ 2\end{array}\right)$ triangles, whose vertices are all in $P$, such that each triangle in $T$ has a side that is not a side of any other triangle in $T$ ?
Answer: There is one possibility for $n=3$ and $n$ possibilities for $n \geqslant 4$.
|
For a fixed point $x \in P$, let $T_{x}$ be the set of all triangles with vertices in $P$ which have $x$ as a vertex. Clearly, $\left|T_{x}\right|=\left(\begin{array}{c}n-1 \\ 2\end{array}\right)$, and each triangle in $T_{x}$ has a side which is not a side of any other triangle in $T_{x}$. For any $x, y \in P$ such that $x \neq y$, we have $T_{x} \neq T_{y}$ if and only if $n \geqslant 4$. We will show that any possible set $T$ is equal to $T_{x}$ for some $x \in P$, i.e. that the answer is 1 for $n=3$ and $n$ for $n \geqslant 4$.
Let
$$
T=\left\{t_{i}: i=1,2, \ldots,\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)\right\}, \quad S=\left\{s_{i}: i=1,2, \ldots,\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)\right\}
$$
such that $T$ is a set of triangles whose vertices are all in $P$, and $s_{i}$ is a side of $t_{i}$ but not of any $t_{j}$, $j \neq i$. Furthermore, let $C$ be the collection of all the $\left(\begin{array}{l}n \\ 3\end{array}\right)$ triangles whose vertices are in $P$. Note that
$$
|C \backslash T|=\left(\begin{array}{c}
n \\
3
\end{array}\right)-\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)=\left(\begin{array}{c}
n-1 \\
3
\end{array}\right)
$$
Let $m$ be the number of pairs $(s, t)$ such that $s \in S$ is a side of $t \in C \backslash T$. Since every $s \in S$ is a side of exactly $n-3$ triangles from $C \backslash T$, we have
$$
m=|S| \cdot(n-3)=\left(\begin{array}{c}
n-1 \\
2
\end{array}\right) \cdot(n-3)=3 \cdot\left(\begin{array}{c}
n-1 \\
3
\end{array}\right)=3 \cdot|C \backslash T|
$$
On the other hand, every $t \in C \backslash T$ has at most three sides from $S$. By the above equality, for every $t \in C \backslash T$, all its sides must be in $S$.
Assume that for $p \in P$ there is a side $s \in S$ such that $p$ is an endpoint of $s$. Then $p$ is also a vertex of each of the $n-3$ triangles in $C \backslash T$ which have $s$ as a side. Consequently, $p$ is an endpoint of $n-2$ sides in $S$. Since every side in $S$ has exactly 2 endpoints, the number of points $p \in P$ which occur as a vertex of some $s \in S$ is
$$
\frac{2 \cdot|S|}{n-2}=\frac{2}{n-2} \cdot\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)=n-1
$$
Consequently, there is an $x \in P$ which is not an endpoint of any $s \in S$, and hence $T$ must be equal to $T_{x}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $P$ be a set of $n \geqslant 3$ points in the plane, no three of which are on a line. How many possibilities are there to choose a set $T$ of $\left(\begin{array}{c}n-1 \\ 2\end{array}\right)$ triangles, whose vertices are all in $P$, such that each triangle in $T$ has a side that is not a side of any other triangle in $T$ ?
Answer: There is one possibility for $n=3$ and $n$ possibilities for $n \geqslant 4$.
|
For a fixed point $x \in P$, let $T_{x}$ be the set of all triangles with vertices in $P$ which have $x$ as a vertex. Clearly, $\left|T_{x}\right|=\left(\begin{array}{c}n-1 \\ 2\end{array}\right)$, and each triangle in $T_{x}$ has a side which is not a side of any other triangle in $T_{x}$. For any $x, y \in P$ such that $x \neq y$, we have $T_{x} \neq T_{y}$ if and only if $n \geqslant 4$. We will show that any possible set $T$ is equal to $T_{x}$ for some $x \in P$, i.e. that the answer is 1 for $n=3$ and $n$ for $n \geqslant 4$.
Let
$$
T=\left\{t_{i}: i=1,2, \ldots,\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)\right\}, \quad S=\left\{s_{i}: i=1,2, \ldots,\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)\right\}
$$
such that $T$ is a set of triangles whose vertices are all in $P$, and $s_{i}$ is a side of $t_{i}$ but not of any $t_{j}$, $j \neq i$. Furthermore, let $C$ be the collection of all the $\left(\begin{array}{l}n \\ 3\end{array}\right)$ triangles whose vertices are in $P$. Note that
$$
|C \backslash T|=\left(\begin{array}{c}
n \\
3
\end{array}\right)-\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)=\left(\begin{array}{c}
n-1 \\
3
\end{array}\right)
$$
Let $m$ be the number of pairs $(s, t)$ such that $s \in S$ is a side of $t \in C \backslash T$. Since every $s \in S$ is a side of exactly $n-3$ triangles from $C \backslash T$, we have
$$
m=|S| \cdot(n-3)=\left(\begin{array}{c}
n-1 \\
2
\end{array}\right) \cdot(n-3)=3 \cdot\left(\begin{array}{c}
n-1 \\
3
\end{array}\right)=3 \cdot|C \backslash T|
$$
On the other hand, every $t \in C \backslash T$ has at most three sides from $S$. By the above equality, for every $t \in C \backslash T$, all its sides must be in $S$.
Assume that for $p \in P$ there is a side $s \in S$ such that $p$ is an endpoint of $s$. Then $p$ is also a vertex of each of the $n-3$ triangles in $C \backslash T$ which have $s$ as a side. Consequently, $p$ is an endpoint of $n-2$ sides in $S$. Since every side in $S$ has exactly 2 endpoints, the number of points $p \in P$ which occur as a vertex of some $s \in S$ is
$$
\frac{2 \cdot|S|}{n-2}=\frac{2}{n-2} \cdot\left(\begin{array}{c}
n-1 \\
2
\end{array}\right)=n-1
$$
Consequently, there is an $x \in P$ which is not an endpoint of any $s \in S$, and hence $T$ must be equal to $T_{x}$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution."
}
|
b0871f2a-e5ba-54a6-a055-35178884780a
| 605,244
|
Two magicians show the following trick. The first magician goes out of the room. The second magician takes a deck of 100 cards labelled by numbers $1,2, \ldots, 100$ and asks three spectators to choose in turn one card each. The second magician sees what card each spectator has taken. Then he adds one more card from the rest of the deck. Spectators shuffle these 4 cards, call the first magician and give him these 4 cards. The first magician looks at the 4 cards and "guesses" what card was chosen by the first spectator, what card by the second and what card by the third. Prove that the magicians can perform this trick.
|
We will identify ourselves with the second magician. Then we need to choose a card in such a manner that another magician will be able to understand which of the 4 cards we have chosen and what information it gives about the order of the other cards. We will reach these two goals independently.
Let $a, b, c$ be remainders of the labels of the spectators' three cards modulo 5 . There are three possible cases.
1) All the three remainders coincide. Then choose a card with a remainder not equal to the remainder of spectators' cards. Denote this remainder $d$.
Note that we now have 2 different remainders, one of them in 3 copies (this will be used by the first magician to distinguish betwwen the three cases). To determine which of the cards is chosen by us is now a simple exercise in division by 5 . But we must also encode the ordering of the spectators' cards. These cards have a natural ordering by their labels, and they are also ordered by their belonging to the spectators. Thus, we have to encode a permutation of 3 elements. There are 6 permutations of 3 elements, let us enumerate them somehow. Then, if we want to inform the first magician that spectators form a permutation number $k$ with respect to the natural ordering, we choose the card number $5 k+d$.
2) The remainders $a, b, c$ are pairwise different. Then it is clear that exactly one of the following possibilities takes place:
$$
\text { either }|b-a|=|a-c| \text {, or }|a-b|=|b-c| \text {, or } \quad|a-c|=|c-b|
$$
(the equalities are considered modulo 5). It is not hard to prove it by a case study, but one could also imagine choosing three vertices of a regular pentagon - these vertices always form an isosceles, but not an equilateral triangle.
Each of these possibilities has one of the remainders distinguished from the other two remainders (these distinguished remainders are $a, b, c$, respectively). Now, choose a card from the rest of the deck having the distinguished remainder modulo 5. Hence, we have three different remainders, one of them distinguished by (9) and presented in two copies. Let $d$ be the distinguished remainder and $s=5 m+d$ be the spectator's card with this remainder.
Now we have to choose a card $r$ with the remainder $d$ such that the first magician would be able to understand which of the cards $s$ and $r$ was chosen by us and what permutation of spectators it implies. This can be done easily: if we want to inform the first magician that spectators form a permutation number $k$ with respect to the natural ordering, we choose the card number $s+5 k(\bmod 100)$.
The decoding procedure is easy: if we have two numbers $p$ and $q$ that have the same remainder modulo 5 , calculate $p-q(\bmod 100)$ and $q-p(\bmod 100)$. If $p-q(\bmod 100)>q-p(\bmod 100)$ then $r=q$ is our card and $s=p$ is the spectator's card. (The case $p-q(\bmod 100)=q-p(\bmod 100)$ is impossible since the sum of these numbers is equal to 100 , and one of them is not greater than $6 \cdot 5=30$.)
3) Two remainders (say, $a$ and $b$ ) coincide. Let us choose a card with the remainder $d=(a+c) / 2 \bmod 5$. Then $|a-d|=|d-c| \bmod 5$, so the remainder $d$ is distinguished by (9). Hence we have three different remainders, one of them distinguished by (9) and one of the non-distinguished remainders presented in two copies. The first magician will easily determine our card, and the rule to choose the card in order to enable him also determine the order of spectators is similar to the one in the 1-st case.
Alternative solution. This solution gives a non-constructive proof that the trick is possible. For this, we need to show there is an injective mapping from the set of ordered triples to the set of unordered quadruples that additionally respects inclusion.
To prove that the desired mapping exists, let's consides a bipartite graph such that the set of ordered triples $T$ and the set of unordered quadruples $Q$ form the two disjoint sets of vertices and there is an edge between a triple and a quadruple if and only if the triple is a subset of the quadruple.
For each triple $t \in T$, we can add any of the remaining 97 cards to it, and thus we have 97 different quadruples connected to each triple in the graph. Conversely, for each quadruple $q \in Q$, we can remove any of the 4 cards from it, and reorder the remaining 3 cards in $3 !=6$ different ways, and thus we have 24 different triples connected to each quadruple in the graph.
According to the Hall's theorem, a bipartite graph $G=(T, Q, E)$ has a perfect matching if and only if for each subset $T^{\prime} \subseteq T$ the set of neighbours of $T^{\prime}$, denoted $N\left(T^{\prime}\right)$, satisfies $\left|N\left(T^{\prime}\right)\right| \geqslant\left|T^{\prime}\right|$.
To prove that this condition holds for our graph, consider any subset $T^{\prime} \subseteq T$. Because we have 97 quadruples for each triple, and there can be at most 24 copies of each of them in the multiset of neighbours, we have $\left|N\left(T^{\prime}\right)\right| \geqslant \frac{97}{24}\left|T^{\prime}\right|>4\left|T^{\prime}\right|$, which is even much more than we need.
Thus, the desired mapping is guaranteed to exist.
Another solution. Let the three chosen numbers be $\left(x_{1}, x_{2}, x_{3}\right)$. At least one of the sets $\{1,2, \ldots, 24\}$, $\{25,26, \ldots, 48\},\{49,50, \ldots, 72\}$ and $\{73,74, \ldots, 96\}$ should contain none of $x_{1}, x_{2}$ and $x_{3}$, let $S$ be such set. Next we split $S$ into 6 parts: $S=S_{1} \cup S_{2} \cup \ldots \cup S_{6}$ so that 4 first elements of $S$ are in $S_{1}$, four next in $S_{2}$, etc. Now we choose $i \in\{1,2, \ldots, 6\}$ corresponding to the order of numbers $x_{1}, x_{2}$ and $x_{3}$ (if $x_{1}<x_{2}<x_{3}$ then $i=1$, if $x_{1}<x_{3}<x_{2}$ then $i=2, \ldots$,if $x_{3}<x_{2}<x_{1}$ then $i=6$ ). At last let $j$ be the number of elements in $\left\{x_{1}, x_{2}, x_{3}\right\}$ that are greater than elements of $S$ (note that any $x_{k}$, $k \in\{1,2,3\}$, is either greater or smaller than all the elements of $S$ ). Now we choose $x_{4} \in S_{i}$ so that $x_{1}+x_{2}+x_{3}+x_{4} \equiv j \bmod 4$ and add the card number $x_{4}$ to those three cards.
Decoding of $\{a, b, c, d\}$ is straightforward. We first put the numbers into increasing order and then calculate $a+b+c+d \bmod 4$ showing the added card. The added card belongs to some $S_{i}(i \in\{1,2, \ldots, 6\})$ for some $S$ and $i$ shows us the initial ordering of cards.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Two magicians show the following trick. The first magician goes out of the room. The second magician takes a deck of 100 cards labelled by numbers $1,2, \ldots, 100$ and asks three spectators to choose in turn one card each. The second magician sees what card each spectator has taken. Then he adds one more card from the rest of the deck. Spectators shuffle these 4 cards, call the first magician and give him these 4 cards. The first magician looks at the 4 cards and "guesses" what card was chosen by the first spectator, what card by the second and what card by the third. Prove that the magicians can perform this trick.
|
We will identify ourselves with the second magician. Then we need to choose a card in such a manner that another magician will be able to understand which of the 4 cards we have chosen and what information it gives about the order of the other cards. We will reach these two goals independently.
Let $a, b, c$ be remainders of the labels of the spectators' three cards modulo 5 . There are three possible cases.
1) All the three remainders coincide. Then choose a card with a remainder not equal to the remainder of spectators' cards. Denote this remainder $d$.
Note that we now have 2 different remainders, one of them in 3 copies (this will be used by the first magician to distinguish betwwen the three cases). To determine which of the cards is chosen by us is now a simple exercise in division by 5 . But we must also encode the ordering of the spectators' cards. These cards have a natural ordering by their labels, and they are also ordered by their belonging to the spectators. Thus, we have to encode a permutation of 3 elements. There are 6 permutations of 3 elements, let us enumerate them somehow. Then, if we want to inform the first magician that spectators form a permutation number $k$ with respect to the natural ordering, we choose the card number $5 k+d$.
2) The remainders $a, b, c$ are pairwise different. Then it is clear that exactly one of the following possibilities takes place:
$$
\text { either }|b-a|=|a-c| \text {, or }|a-b|=|b-c| \text {, or } \quad|a-c|=|c-b|
$$
(the equalities are considered modulo 5). It is not hard to prove it by a case study, but one could also imagine choosing three vertices of a regular pentagon - these vertices always form an isosceles, but not an equilateral triangle.
Each of these possibilities has one of the remainders distinguished from the other two remainders (these distinguished remainders are $a, b, c$, respectively). Now, choose a card from the rest of the deck having the distinguished remainder modulo 5. Hence, we have three different remainders, one of them distinguished by (9) and presented in two copies. Let $d$ be the distinguished remainder and $s=5 m+d$ be the spectator's card with this remainder.
Now we have to choose a card $r$ with the remainder $d$ such that the first magician would be able to understand which of the cards $s$ and $r$ was chosen by us and what permutation of spectators it implies. This can be done easily: if we want to inform the first magician that spectators form a permutation number $k$ with respect to the natural ordering, we choose the card number $s+5 k(\bmod 100)$.
The decoding procedure is easy: if we have two numbers $p$ and $q$ that have the same remainder modulo 5 , calculate $p-q(\bmod 100)$ and $q-p(\bmod 100)$. If $p-q(\bmod 100)>q-p(\bmod 100)$ then $r=q$ is our card and $s=p$ is the spectator's card. (The case $p-q(\bmod 100)=q-p(\bmod 100)$ is impossible since the sum of these numbers is equal to 100 , and one of them is not greater than $6 \cdot 5=30$.)
3) Two remainders (say, $a$ and $b$ ) coincide. Let us choose a card with the remainder $d=(a+c) / 2 \bmod 5$. Then $|a-d|=|d-c| \bmod 5$, so the remainder $d$ is distinguished by (9). Hence we have three different remainders, one of them distinguished by (9) and one of the non-distinguished remainders presented in two copies. The first magician will easily determine our card, and the rule to choose the card in order to enable him also determine the order of spectators is similar to the one in the 1-st case.
Alternative solution. This solution gives a non-constructive proof that the trick is possible. For this, we need to show there is an injective mapping from the set of ordered triples to the set of unordered quadruples that additionally respects inclusion.
To prove that the desired mapping exists, let's consides a bipartite graph such that the set of ordered triples $T$ and the set of unordered quadruples $Q$ form the two disjoint sets of vertices and there is an edge between a triple and a quadruple if and only if the triple is a subset of the quadruple.
For each triple $t \in T$, we can add any of the remaining 97 cards to it, and thus we have 97 different quadruples connected to each triple in the graph. Conversely, for each quadruple $q \in Q$, we can remove any of the 4 cards from it, and reorder the remaining 3 cards in $3 !=6$ different ways, and thus we have 24 different triples connected to each quadruple in the graph.
According to the Hall's theorem, a bipartite graph $G=(T, Q, E)$ has a perfect matching if and only if for each subset $T^{\prime} \subseteq T$ the set of neighbours of $T^{\prime}$, denoted $N\left(T^{\prime}\right)$, satisfies $\left|N\left(T^{\prime}\right)\right| \geqslant\left|T^{\prime}\right|$.
To prove that this condition holds for our graph, consider any subset $T^{\prime} \subseteq T$. Because we have 97 quadruples for each triple, and there can be at most 24 copies of each of them in the multiset of neighbours, we have $\left|N\left(T^{\prime}\right)\right| \geqslant \frac{97}{24}\left|T^{\prime}\right|>4\left|T^{\prime}\right|$, which is even much more than we need.
Thus, the desired mapping is guaranteed to exist.
Another solution. Let the three chosen numbers be $\left(x_{1}, x_{2}, x_{3}\right)$. At least one of the sets $\{1,2, \ldots, 24\}$, $\{25,26, \ldots, 48\},\{49,50, \ldots, 72\}$ and $\{73,74, \ldots, 96\}$ should contain none of $x_{1}, x_{2}$ and $x_{3}$, let $S$ be such set. Next we split $S$ into 6 parts: $S=S_{1} \cup S_{2} \cup \ldots \cup S_{6}$ so that 4 first elements of $S$ are in $S_{1}$, four next in $S_{2}$, etc. Now we choose $i \in\{1,2, \ldots, 6\}$ corresponding to the order of numbers $x_{1}, x_{2}$ and $x_{3}$ (if $x_{1}<x_{2}<x_{3}$ then $i=1$, if $x_{1}<x_{3}<x_{2}$ then $i=2, \ldots$,if $x_{3}<x_{2}<x_{1}$ then $i=6$ ). At last let $j$ be the number of elements in $\left\{x_{1}, x_{2}, x_{3}\right\}$ that are greater than elements of $S$ (note that any $x_{k}$, $k \in\{1,2,3\}$, is either greater or smaller than all the elements of $S$ ). Now we choose $x_{4} \in S_{i}$ so that $x_{1}+x_{2}+x_{3}+x_{4} \equiv j \bmod 4$ and add the card number $x_{4}$ to those three cards.
Decoding of $\{a, b, c, d\}$ is straightforward. We first put the numbers into increasing order and then calculate $a+b+c+d \bmod 4$ showing the added card. The added card belongs to some $S_{i}(i \in\{1,2, \ldots, 6\})$ for some $S$ and $i$ shows us the initial ordering of cards.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\nSolution."
}
|
5898405f-230b-5e14-adf0-fa706f207ce8
| 236,593
|
Let $N$ be a positive integer. Two persons play the following game. The first player writes a list of positive integers not greater than 25 , not necessarily different, such that their sum is at least 200 . The second player wins if he can select some of these numbers so that their sum $S$ satisfies the condition $200-N \leqslant S \leqslant 200+N$. What is the smallest value of $N$ for which the second player has a winning strategy?
Answer: $N=11$.
|
If $N=11$, then the second player can simply remove numbers from the list, starting with the smallest number, until the sum of the remaining numbers is less than 212. If the last number removed was not 24 or 25 , then the sum of the remaining numbers is at least $212-23=189$. If the last number removed was 24 or 25 , then only 24 -s and 25 -s remain, and there must be exactly 8 of them since their sum must be less than 212 and not less than $212-24=188$. Hence their sum $S$ satisfies $8 \cdot 24=192 \leqslant S \leqslant 8 \cdot 25=200$. In any case the second player wins.
On the other hand, if $N \leqslant 10$, then the first player can write 25 two times and 23 seven times. Then the sum of all numbers is 211 , but if at least one number is removed, then the sum of the remaining ones is at most 188 - so the second player cannot win.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $N$ be a positive integer. Two persons play the following game. The first player writes a list of positive integers not greater than 25 , not necessarily different, such that their sum is at least 200 . The second player wins if he can select some of these numbers so that their sum $S$ satisfies the condition $200-N \leqslant S \leqslant 200+N$. What is the smallest value of $N$ for which the second player has a winning strategy?
Answer: $N=11$.
|
If $N=11$, then the second player can simply remove numbers from the list, starting with the smallest number, until the sum of the remaining numbers is less than 212. If the last number removed was not 24 or 25 , then the sum of the remaining numbers is at least $212-23=189$. If the last number removed was 24 or 25 , then only 24 -s and 25 -s remain, and there must be exactly 8 of them since their sum must be less than 212 and not less than $212-24=188$. Hence their sum $S$ satisfies $8 \cdot 24=192 \leqslant S \leqslant 8 \cdot 25=200$. In any case the second player wins.
On the other hand, if $N \leqslant 10$, then the first player can write 25 two times and 23 seven times. Then the sum of all numbers is 211 , but if at least one number is removed, then the sum of the remaining ones is at most 188 - so the second player cannot win.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\nSolution."
}
|
40bc2cb2-0cd2-52be-b8b4-d9deb7870e3b
| 605,278
|
Let $n$ be a positive integer. Consider $n$ points in the plane such that no three of them are collinear and no two of the distances between them are equal. One by one, we connect each point to the two points nearest to it by line segments (if there are already other line segments drawn to this point, we do not erase these). Prove that there is no point from which line segments will be drawn to more than 11 points.
|
Suppose there exists a point $A$ such that $A$ is connected to twelve points. Then there exist three points $B, C$ and $D$ such that $\angle B A C \leqslant 60^{\circ}, \angle B A D \leqslant 60^{\circ}$ and $\angle C A D \leqslant 60^{\circ}$.
We can assume that $|A D|>|A B|$ and $|A D|>|A C|$. By the cosine law we have
$$
\begin{aligned}
|B D|^{2} & =|A D|^{2}+|A B|^{2}-2|A D \| A B| \cos \angle B A D \\
& <|A D|^{2}+|A B|^{2}-2|A B|^{2} \cos \angle B A D \\
& =|A D|^{2}+|A B|^{2}(1-2 \cos \angle B A D) \\
& \leqslant|A D|^{2}
\end{aligned}
$$
since $1 \leqslant 2 \cos (\angle B A D)$. Hence $|B D|<|A D|$. Similarly we get $|C D|<|A D|$. Hence $A$ and $D$ should not be connected which is a contradiction.
Comment. It would be interesting to know whether 11 can be achieved or the actual bound is lower.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Consider $n$ points in the plane such that no three of them are collinear and no two of the distances between them are equal. One by one, we connect each point to the two points nearest to it by line segments (if there are already other line segments drawn to this point, we do not erase these). Prove that there is no point from which line segments will be drawn to more than 11 points.
|
Suppose there exists a point $A$ such that $A$ is connected to twelve points. Then there exist three points $B, C$ and $D$ such that $\angle B A C \leqslant 60^{\circ}, \angle B A D \leqslant 60^{\circ}$ and $\angle C A D \leqslant 60^{\circ}$.
We can assume that $|A D|>|A B|$ and $|A D|>|A C|$. By the cosine law we have
$$
\begin{aligned}
|B D|^{2} & =|A D|^{2}+|A B|^{2}-2|A D \| A B| \cos \angle B A D \\
& <|A D|^{2}+|A B|^{2}-2|A B|^{2} \cos \angle B A D \\
& =|A D|^{2}+|A B|^{2}(1-2 \cos \angle B A D) \\
& \leqslant|A D|^{2}
\end{aligned}
$$
since $1 \leqslant 2 \cos (\angle B A D)$. Hence $|B D|<|A D|$. Similarly we get $|C D|<|A D|$. Hence $A$ and $D$ should not be connected which is a contradiction.
Comment. It would be interesting to know whether 11 can be achieved or the actual bound is lower.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution."
}
|
055f4761-3661-5948-a320-8854ae5316a3
| 236,610
|
A set $S$ of four distinct points is given in the plane. It is known that for any point $X \in S$ the remaining points can be denoted by $Y, Z$ and $W$ so that
$$
|X Y|=|X Z|+|X W| .
$$
Prove that all the four points lie on a line.
|
Let $S=\{A, B, C, D\}$ and let $A B$ be the longest of the six segments formed by these four points (if there are several longest segments, choose any of them). If we choose $X=A$ then we must also choose $Y=B$. Indeed, if we would, for example, choose $Y=C$, we should have $|A C|=|A B|+|A D|$ contradicting the maximality of $A B$. Hence we get
$$
|A B|=|A C|+|A D| \text {. }
$$
Similarly, choosing $X=B$ we must choose $Y=A$ and we obtain
$$
|A B|=|B C|+|B D| \text {. }
$$
On the other hand, from the triangle inequality we know that
$$
\begin{aligned}
& |A B| \leqslant|A C|+|B C|, \\
& |A B| \leqslant|A D|+|B D|,
\end{aligned}
$$
where at least one of the inequalities is strict if all the four points are not on the same line. Hence, adding the two last inequalities we get
$$
2|A B|<|A C|+|B C|+|A D|+|B D| .
$$
On the other hand, adding (10) and (11) we get
$$
2|A B|=|A C|+|A D|+|B C|+|B D|,
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A set $S$ of four distinct points is given in the plane. It is known that for any point $X \in S$ the remaining points can be denoted by $Y, Z$ and $W$ so that
$$
|X Y|=|X Z|+|X W| .
$$
Prove that all the four points lie on a line.
|
Let $S=\{A, B, C, D\}$ and let $A B$ be the longest of the six segments formed by these four points (if there are several longest segments, choose any of them). If we choose $X=A$ then we must also choose $Y=B$. Indeed, if we would, for example, choose $Y=C$, we should have $|A C|=|A B|+|A D|$ contradicting the maximality of $A B$. Hence we get
$$
|A B|=|A C|+|A D| \text {. }
$$
Similarly, choosing $X=B$ we must choose $Y=A$ and we obtain
$$
|A B|=|B C|+|B D| \text {. }
$$
On the other hand, from the triangle inequality we know that
$$
\begin{aligned}
& |A B| \leqslant|A C|+|B C|, \\
& |A B| \leqslant|A D|+|B D|,
\end{aligned}
$$
where at least one of the inequalities is strict if all the four points are not on the same line. Hence, adding the two last inequalities we get
$$
2|A B|<|A C|+|B C|+|A D|+|B D| .
$$
On the other hand, adding (10) and (11) we get
$$
2|A B|=|A C|+|A D|+|B C|+|B D|,
$$
a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution."
}
|
cf70de46-0caf-5644-86b2-39927420ea06
| 236,623
|
Let $A B C$ be an acute triangle with $\angle B A C>\angle B C A$, and let $D$ be a point on side $A C$ such that $|A B|=|B D|$. Furthermore, let $F$ be a point on the circumcircle of triangle $A B C$ such that line $F D$ is perpendicular to side $B C$ and points $F, B$ lie on different sides of line $A C$. Prove that line $F B$ is perpendicular to side $A C$.
|
Let $E$ be the other point on the circumcircle of triangle $A B C$ such that $|A B|=|E B|$. Let $D^{\prime}$ be the point of intersection of side $A C$ and the line perpendicular to side $B C$, passing through $E$. Then $\angle E C B=\angle B C A$ and the triangle $E C D^{\prime}$ is isosceles. As $E D^{\prime} \perp B C$, the triangle $B E D^{\prime}$ is also isosceles and $|B E|=\left|B D^{\prime}\right|$ implying $D=D^{\prime}$. Hence, the points $E, D, F$ lie on one line. We now have
$$
\angle E F B+\angle F D A=\angle B C A+\angle E D C=90^{\circ} .
$$
The required result now follows.
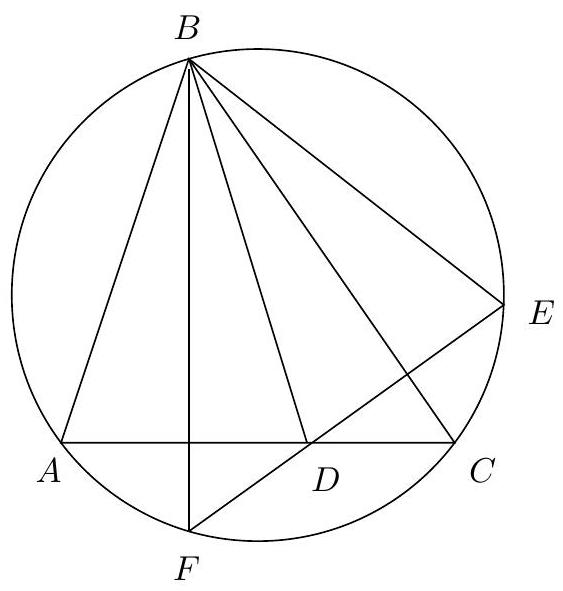
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $\angle B A C>\angle B C A$, and let $D$ be a point on side $A C$ such that $|A B|=|B D|$. Furthermore, let $F$ be a point on the circumcircle of triangle $A B C$ such that line $F D$ is perpendicular to side $B C$ and points $F, B$ lie on different sides of line $A C$. Prove that line $F B$ is perpendicular to side $A C$.
|
Let $E$ be the other point on the circumcircle of triangle $A B C$ such that $|A B|=|E B|$. Let $D^{\prime}$ be the point of intersection of side $A C$ and the line perpendicular to side $B C$, passing through $E$. Then $\angle E C B=\angle B C A$ and the triangle $E C D^{\prime}$ is isosceles. As $E D^{\prime} \perp B C$, the triangle $B E D^{\prime}$ is also isosceles and $|B E|=\left|B D^{\prime}\right|$ implying $D=D^{\prime}$. Hence, the points $E, D, F$ lie on one line. We now have
$$
\angle E F B+\angle F D A=\angle B C A+\angle E D C=90^{\circ} .
$$
The required result now follows.

|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution."
}
|
16167e1c-4767-5152-a738-450299aef276
| 236,631
|
Let $L, M$ and $N$ be points on sides $A C, A B$ and $B C$ of triangle $A B C$, respectively, such that $B L$ is the bisector of angle $A B C$ and segments $A N, B L$ and $C M$ have a common point. Prove that if $\angle A L B=\angle M N B$ then $\angle L N M=90^{\circ}$.
|
Let $P$ be the intersection point of lines $M N$ and $A C$. Then $\angle P L B=\angle P N B$ and the quadrangle $P L N B$ is cyclic. Let $\omega$ be its circumcircle. It is sufficient to prove that $P L$ is a diameter of $\omega$.
Let $Q$ denote the second intersection point of the line $A B$ and $\omega$. Then $\angle P Q B=\angle P L B$ and
$$
\angle Q P L=\angle Q B L=\angle L B N=\angle L P N
$$
and the triangles $P A Q$ and $B A L$ are similar. Therefore,
$$
\frac{|P Q|}{|P A|}=\frac{|B L|}{|B A|}
$$
We see that the line $P L$ is a bisector of the inscribed angle $N P Q$. Now in order to prove that $P L$ is a diameter of $\omega$ it is sufficient to check that $|P N|=|P Q|$.
The triangles $N P C$ and $L B C$ are similar, hence
$$
\frac{|P N|}{|P C|}=\frac{|B L|}{|B C|}
$$
Note also that
$$
\frac{|A B|}{|B C|}=\frac{|A L|}{|C L|}
$$
by the properties of a bisector. Combining (12), (13) and (14) we have
$$
\frac{|P N|}{|P Q|}=\frac{|A L|}{|A P|} \cdot \frac{|C P|}{|C L|}
$$
We want to prove that the left hand side of this equality equals 1 . This follows from the fact that the quadruple of points $(P, A, L, C)$ is harmonic, as can be proven using standard methods (e.g. considering the quadrilateral $M B N S$, where $S=M C \cap A N$ ).
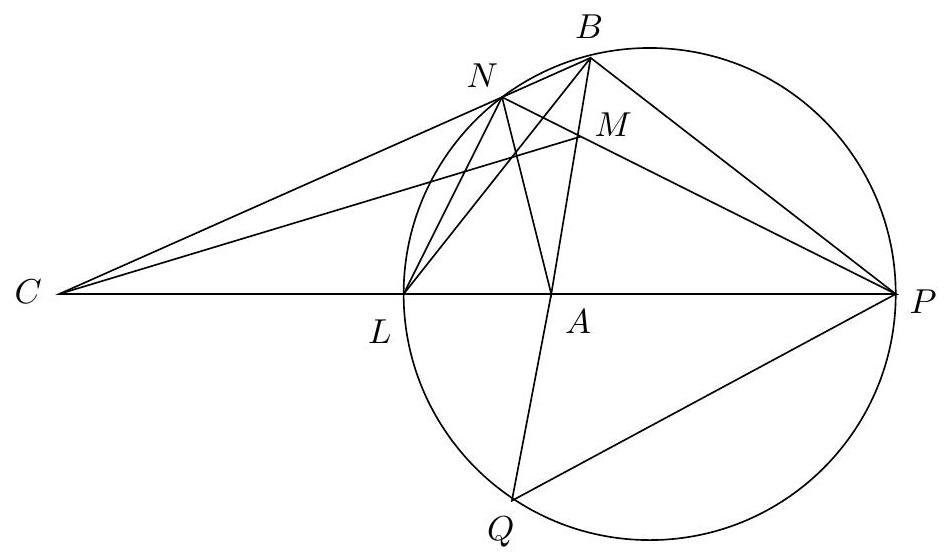
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $L, M$ and $N$ be points on sides $A C, A B$ and $B C$ of triangle $A B C$, respectively, such that $B L$ is the bisector of angle $A B C$ and segments $A N, B L$ and $C M$ have a common point. Prove that if $\angle A L B=\angle M N B$ then $\angle L N M=90^{\circ}$.
|
Let $P$ be the intersection point of lines $M N$ and $A C$. Then $\angle P L B=\angle P N B$ and the quadrangle $P L N B$ is cyclic. Let $\omega$ be its circumcircle. It is sufficient to prove that $P L$ is a diameter of $\omega$.
Let $Q$ denote the second intersection point of the line $A B$ and $\omega$. Then $\angle P Q B=\angle P L B$ and
$$
\angle Q P L=\angle Q B L=\angle L B N=\angle L P N
$$
and the triangles $P A Q$ and $B A L$ are similar. Therefore,
$$
\frac{|P Q|}{|P A|}=\frac{|B L|}{|B A|}
$$
We see that the line $P L$ is a bisector of the inscribed angle $N P Q$. Now in order to prove that $P L$ is a diameter of $\omega$ it is sufficient to check that $|P N|=|P Q|$.
The triangles $N P C$ and $L B C$ are similar, hence
$$
\frac{|P N|}{|P C|}=\frac{|B L|}{|B C|}
$$
Note also that
$$
\frac{|A B|}{|B C|}=\frac{|A L|}{|C L|}
$$
by the properties of a bisector. Combining (12), (13) and (14) we have
$$
\frac{|P N|}{|P Q|}=\frac{|A L|}{|A P|} \cdot \frac{|C P|}{|C L|}
$$
We want to prove that the left hand side of this equality equals 1 . This follows from the fact that the quadruple of points $(P, A, L, C)$ is harmonic, as can be proven using standard methods (e.g. considering the quadrilateral $M B N S$, where $S=M C \cap A N$ ).

|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution."
}
|
f246a15c-14fd-5b32-ae72-64e8a0b8b6b4
| 236,641
|
A spider and a fly are sitting on a cube. The fly wants to maximize the shortest path to the spider along the surface of the cube. Is it necessarily best for the fly to be at the point opposite to the spider? ("Opposite" means "symmetric with respect to the center of the cube".)
Answer: no.
|
Suppose that the side of the cube is 1 and the spider sits at the middle of one of the edges. Then the shortest path to the middle of the opposite edge has length 2 . However, if the fly goes to a point on this edge at distance $s$ from the middle, then the length of the shortest path is
$$
\min \left(\sqrt{4+s^{2}}, \sqrt{\frac{9}{4}+\left(\frac{3}{2}-s\right)^{2}}\right) .
$$
If $0<s<(3-\sqrt{7}) / 2$ then this expression is greater than 2 .
|
0<s<(3-\sqrt{7}) / 2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A spider and a fly are sitting on a cube. The fly wants to maximize the shortest path to the spider along the surface of the cube. Is it necessarily best for the fly to be at the point opposite to the spider? ("Opposite" means "symmetric with respect to the center of the cube".)
Answer: no.
|
Suppose that the side of the cube is 1 and the spider sits at the middle of one of the edges. Then the shortest path to the middle of the opposite edge has length 2 . However, if the fly goes to a point on this edge at distance $s$ from the middle, then the length of the shortest path is
$$
\min \left(\sqrt{4+s^{2}}, \sqrt{\frac{9}{4}+\left(\frac{3}{2}-s\right)^{2}}\right) .
$$
If $0<s<(3-\sqrt{7}) / 2$ then this expression is greater than 2 .
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n15.",
"solution_match": "\nSolution."
}
|
0147b9a1-f37d-59d4-8f1d-06a6053e6615
| 236,650
|
Find all nonnegative integers $m$ such that
$$
a_{m}=\left(2^{2 m+1}\right)^{2}+1
$$
is divisible by at most two different primes.
Answer: $m=0,1,2$ are the only solutions.
|
Obviously $m=0,1,2$ are solutions as $a_{0}=5, a_{1}=65=5 \cdot 13$, and $a_{2}=1025=25 \cdot 41$. We show that these are the only solutions.
Assume that $m \geqslant 3$ and that $a_{m}$ contains at most two different prime factors. Clearly, $a_{m}=4^{2 m+1}+1$ is divisible by 5 , and
$$
a_{m}=\left(2^{2 m+1}+2^{m+1}+1\right) \cdot\left(2^{2 m+1}-2^{m+1}+1\right) \text {. }
$$
The two above factors are relatively prime as they are both odd and their difference is a power of 2 . Since both factors are larger than 1 , one of them must be a power of 5 . Hence,
$$
2^{m+1} \cdot\left(2^{m} \pm 1\right)=5^{t}-1=(5-1) \cdot\left(1+5+\cdots+5^{t-1}\right)
$$
for some positive integer $t$, where $\pm$ reads as either plus or minus. For odd $t$ the right hand side is not divisible by 8 , contradicting $m \geqslant 3$. Therefore, $t$ must be even and
$$
2^{m+1} \cdot\left(2^{m} \pm 1\right)=\left(5^{t / 2}-1\right) \cdot\left(5^{t / 2}+1\right) .
$$
Clearly, $5^{t / 2}+1 \equiv 2(\bmod 4)$. Consequently, $5^{t / 2}-1=2^{m} \cdot k$ for some odd $k$, and $5^{t / 2}+1=2^{m} \cdot k+2$ divides $2\left(2^{m} \pm 1\right)$, i.e.
$$
2^{m-1} \cdot k+1 \mid 2^{m} \pm 1 .
$$
This implies $k=1$, finally leading to a contradiction since
$$
2^{m-1}+1<2^{m} \pm 1<2\left(2^{m-1}+1\right)
$$
for $m \geqslant 3$.
|
m=0,1,2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all nonnegative integers $m$ such that
$$
a_{m}=\left(2^{2 m+1}\right)^{2}+1
$$
is divisible by at most two different primes.
Answer: $m=0,1,2$ are the only solutions.
|
Obviously $m=0,1,2$ are solutions as $a_{0}=5, a_{1}=65=5 \cdot 13$, and $a_{2}=1025=25 \cdot 41$. We show that these are the only solutions.
Assume that $m \geqslant 3$ and that $a_{m}$ contains at most two different prime factors. Clearly, $a_{m}=4^{2 m+1}+1$ is divisible by 5 , and
$$
a_{m}=\left(2^{2 m+1}+2^{m+1}+1\right) \cdot\left(2^{2 m+1}-2^{m+1}+1\right) \text {. }
$$
The two above factors are relatively prime as they are both odd and their difference is a power of 2 . Since both factors are larger than 1 , one of them must be a power of 5 . Hence,
$$
2^{m+1} \cdot\left(2^{m} \pm 1\right)=5^{t}-1=(5-1) \cdot\left(1+5+\cdots+5^{t-1}\right)
$$
for some positive integer $t$, where $\pm$ reads as either plus or minus. For odd $t$ the right hand side is not divisible by 8 , contradicting $m \geqslant 3$. Therefore, $t$ must be even and
$$
2^{m+1} \cdot\left(2^{m} \pm 1\right)=\left(5^{t / 2}-1\right) \cdot\left(5^{t / 2}+1\right) .
$$
Clearly, $5^{t / 2}+1 \equiv 2(\bmod 4)$. Consequently, $5^{t / 2}-1=2^{m} \cdot k$ for some odd $k$, and $5^{t / 2}+1=2^{m} \cdot k+2$ divides $2\left(2^{m} \pm 1\right)$, i.e.
$$
2^{m-1} \cdot k+1 \mid 2^{m} \pm 1 .
$$
This implies $k=1$, finally leading to a contradiction since
$$
2^{m-1}+1<2^{m} \pm 1<2\left(2^{m-1}+1\right)
$$
for $m \geqslant 3$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n16.",
"solution_match": "\nSolution."
}
|
a972c36a-ebf6-502a-b2d3-7d4e124a0264
| 236,660
|
Show that the sequence
$$
\left(\begin{array}{l}
2002 \\
2002
\end{array}\right),\left(\begin{array}{c}
2003 \\
2002
\end{array}\right),\left(\begin{array}{l}
2004 \\
2002
\end{array}\right), \ldots
$$
considered modulo 2002, is periodic.
|
Define
$$
x_{n}^{k}=\left(\begin{array}{l}
n \\
k
\end{array}\right)
$$
and note that
$$
x_{n+1}^{k}-x_{n}^{k}=\left(\begin{array}{c}
n+1 \\
k
\end{array}\right)-\left(\begin{array}{l}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n \\
k-1
\end{array}\right)=x_{n}^{k-1}
$$
Let $m$ be any positive integer. We will prove by induction on $k$ that the sequence $\left\{x_{n}^{k}\right\}_{n=k}^{\infty}$ is periodic modulo $m$. For $k=1$ it is obvious that $x_{n}^{k}=n$ is periodic modulo $m$ with period $m$. Therefore it will suffice to show that the following is true: the sequence $\left\{x_{n}\right\}$ is periodic modulo $m$ if its difference sequence, $d_{n}=x_{n+1}-x_{n}$, is periodic modulo $m$.
Furthermore, if $t$ then the period of $\left\{x_{n}\right\}$ is equal to $h t$ where $h$ is the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$.
Indeed, let $t$ be the period of $\left\{d_{n}\right\}$ and $h$ be the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$. Then
$$
\begin{aligned}
x_{n+h t} & =x_{0}+\sum_{j=0}^{n+h t-1} d_{j}=x_{0}+\sum_{j=0}^{n-1} d_{j}+h\left(\sum_{j=0}^{t-1} d_{j}\right)= \\
& =x_{n}+h\left(x_{t}-x_{0}\right) \equiv x_{n}(\bmod m)
\end{aligned}
$$
for all $n$, so the sequence $\left\{x_{n}\right\}$ is in fact periodic modulo $m$ (with a period dividing $h t$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that the sequence
$$
\left(\begin{array}{l}
2002 \\
2002
\end{array}\right),\left(\begin{array}{c}
2003 \\
2002
\end{array}\right),\left(\begin{array}{l}
2004 \\
2002
\end{array}\right), \ldots
$$
considered modulo 2002, is periodic.
|
Define
$$
x_{n}^{k}=\left(\begin{array}{l}
n \\
k
\end{array}\right)
$$
and note that
$$
x_{n+1}^{k}-x_{n}^{k}=\left(\begin{array}{c}
n+1 \\
k
\end{array}\right)-\left(\begin{array}{l}
n \\
k
\end{array}\right)=\left(\begin{array}{c}
n \\
k-1
\end{array}\right)=x_{n}^{k-1}
$$
Let $m$ be any positive integer. We will prove by induction on $k$ that the sequence $\left\{x_{n}^{k}\right\}_{n=k}^{\infty}$ is periodic modulo $m$. For $k=1$ it is obvious that $x_{n}^{k}=n$ is periodic modulo $m$ with period $m$. Therefore it will suffice to show that the following is true: the sequence $\left\{x_{n}\right\}$ is periodic modulo $m$ if its difference sequence, $d_{n}=x_{n+1}-x_{n}$, is periodic modulo $m$.
Furthermore, if $t$ then the period of $\left\{x_{n}\right\}$ is equal to $h t$ where $h$ is the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$.
Indeed, let $t$ be the period of $\left\{d_{n}\right\}$ and $h$ be the smallest positive integer such that $h\left(x_{t}-x_{0}\right) \equiv 0$ modulo $m$. Then
$$
\begin{aligned}
x_{n+h t} & =x_{0}+\sum_{j=0}^{n+h t-1} d_{j}=x_{0}+\sum_{j=0}^{n-1} d_{j}+h\left(\sum_{j=0}^{t-1} d_{j}\right)= \\
& =x_{n}+h\left(x_{t}-x_{0}\right) \equiv x_{n}(\bmod m)
\end{aligned}
$$
for all $n$, so the sequence $\left\{x_{n}\right\}$ is in fact periodic modulo $m$ (with a period dividing $h t$ ).
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n17.",
"solution_match": "\nSolution."
}
|
f852e7b6-0bb4-56dd-9f1c-baebd24d6adf
| 236,669
|
Find all integers $n>1$ such that any prime divisor of $n^{6}-1$ is a divisor of $\left(n^{3}-1\right)\left(n^{2}-1\right)$.
|
Clearly $n=2$ is such an integer. We will show that there are no others.
Consider the equality
$$
n^{6}-1=\left(n^{2}-n+1\right)(n+1)\left(n^{3}-1\right) \text {. }
$$
The integer $n^{2}-n+1=n(n-1)+1$ clearly has an odd divisor $p$. Then $p \mid n^{3}+1$. Therefore, $p$ does not divide $n^{3}-1$ and consequently $p \mid n^{2}-1$. This implies that $p$ divides $\left(n^{3}+1\right)+\left(n^{2}-1\right)=n^{2}(n+1)$. As $p$ does not divide $n$, we obtain $p \mid n+1$. Also, $p \mid\left(n^{2}-1\right)-\left(n^{2}-n+1\right)=n-2$. From $p \mid n+1$ and $p \mid n-2$ it follows that $p=3$, so $n^{2}-n+1=3^{r}$ for some positive integer $r$.
The discriminant of the quadratic $n^{2}-n+\left(1-3^{r}\right)$ must be a square of an integer, hence
$$
1-4\left(1-3^{r}\right)=3\left(4 \cdot 3^{r-1}-1\right)
$$
must be a squareof an integer. Since for $r \geqslant 2$ the number $4 \cdot 3^{r-1}-1$ is not divisible by 3 , this is possible only if $r=1$. So $n^{2}-n-2=0$ and $n=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all integers $n>1$ such that any prime divisor of $n^{6}-1$ is a divisor of $\left(n^{3}-1\right)\left(n^{2}-1\right)$.
|
Clearly $n=2$ is such an integer. We will show that there are no others.
Consider the equality
$$
n^{6}-1=\left(n^{2}-n+1\right)(n+1)\left(n^{3}-1\right) \text {. }
$$
The integer $n^{2}-n+1=n(n-1)+1$ clearly has an odd divisor $p$. Then $p \mid n^{3}+1$. Therefore, $p$ does not divide $n^{3}-1$ and consequently $p \mid n^{2}-1$. This implies that $p$ divides $\left(n^{3}+1\right)+\left(n^{2}-1\right)=n^{2}(n+1)$. As $p$ does not divide $n$, we obtain $p \mid n+1$. Also, $p \mid\left(n^{2}-1\right)-\left(n^{2}-n+1\right)=n-2$. From $p \mid n+1$ and $p \mid n-2$ it follows that $p=3$, so $n^{2}-n+1=3^{r}$ for some positive integer $r$.
The discriminant of the quadratic $n^{2}-n+\left(1-3^{r}\right)$ must be a square of an integer, hence
$$
1-4\left(1-3^{r}\right)=3\left(4 \cdot 3^{r-1}-1\right)
$$
must be a squareof an integer. Since for $r \geqslant 2$ the number $4 \cdot 3^{r-1}-1$ is not divisible by 3 , this is possible only if $r=1$. So $n^{2}-n-2=0$ and $n=2$.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n18.",
"solution_match": "\nSolution."
}
|
c75e15e7-4f9a-5dc1-9816-4ec3c9b864a0
| 236,678
|
Let $n$ be a positive integer. Prove that the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}=3 n
$$
does not have solutions in positive rational numbers.
|
Suppose $x=\frac{p}{q}$ and $y=\frac{r}{s}$ satisfy the given equation, where $p, q, r, s$ are positive integers and $\operatorname{gcd}(p, q)=1, \operatorname{gcd}(r, s)=1$. We have
$$
\frac{p}{q}+\frac{r}{s}+\frac{q}{p}+\frac{s}{r}=3 n
$$
or
$$
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) p q=3 n p q r s,
$$
so $r s \mid\left(r^{2}+s^{2}\right) p q$. Since $\operatorname{gcd}(r, s)=1$, we have $\operatorname{gcd}\left(r^{2}+s^{2}, r s\right)=1$ and $r s \mid p q$. Analogously $p q \mid r s$, so $r s=p q$ and hence there are either two or zero integers divisible by 3 among $p, q, r, s$. Now we have
$$
\begin{aligned}
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) r s & =3 n(r s)^{2} \\
p^{2}+q^{2}+r^{2}+s^{2} & =3 n r s,
\end{aligned}
$$
but $3 n r s \equiv 0(\bmod 3)$ and $p^{2}+q^{2}+r^{2}+s^{2}$ is congruent to either 1 or 2 modulo 3 , a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer. Prove that the equation
$$
x+y+\frac{1}{x}+\frac{1}{y}=3 n
$$
does not have solutions in positive rational numbers.
|
Suppose $x=\frac{p}{q}$ and $y=\frac{r}{s}$ satisfy the given equation, where $p, q, r, s$ are positive integers and $\operatorname{gcd}(p, q)=1, \operatorname{gcd}(r, s)=1$. We have
$$
\frac{p}{q}+\frac{r}{s}+\frac{q}{p}+\frac{s}{r}=3 n
$$
or
$$
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) p q=3 n p q r s,
$$
so $r s \mid\left(r^{2}+s^{2}\right) p q$. Since $\operatorname{gcd}(r, s)=1$, we have $\operatorname{gcd}\left(r^{2}+s^{2}, r s\right)=1$ and $r s \mid p q$. Analogously $p q \mid r s$, so $r s=p q$ and hence there are either two or zero integers divisible by 3 among $p, q, r, s$. Now we have
$$
\begin{aligned}
\left(p^{2}+q^{2}\right) r s+\left(r^{2}+s^{2}\right) r s & =3 n(r s)^{2} \\
p^{2}+q^{2}+r^{2}+s^{2} & =3 n r s,
\end{aligned}
$$
but $3 n r s \equiv 0(\bmod 3)$ and $p^{2}+q^{2}+r^{2}+s^{2}$ is congruent to either 1 or 2 modulo 3 , a contradiction.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n19.",
"solution_match": "\nSolution."
}
|
38425ca8-71e6-5970-a0fd-0c17305c1ef1
| 605,439
|
Does there exist an infinite non-constant arithmetic progression, each term of which is of the form $a^{b}$, where $a$ and $b$ are positive integers with $b \geqslant 2$ ?
Answer: no.
|
For an arithmetic progression $a_{1}, a_{2}, \ldots$ with difference $d$ the following holds:
$$
\begin{aligned}
S_{n} & =\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n+1}}=\frac{1}{a_{1}}+\frac{1}{a_{1}+d}+\ldots+\frac{1}{a_{1}+n d} \geqslant \\
& \geqslant \frac{1}{m}\left(\frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{n+1}\right),
\end{aligned}
$$
where $m=\max \left(a_{1}, d\right)$. Therefore $S_{n}$ tends to infinity when $n$ increases.
On the other hand, the sum of reciprocals of the powers of a natural number $x \neq 1$ is
$$
\frac{1}{x^{2}}+\frac{1}{x^{3}}+\ldots=\frac{\frac{1}{x^{2}}}{1-\frac{1}{x}}=\frac{1}{x(x-1)}
$$
Hence, the sum of reciprocals of the terms of the progression required in the problem cannot exceed
$$
\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots=1+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\ldots\right)=2
$$
a contradiction.
Alternative solution. Let $a_{k}=a_{0}+d k, k=0,1, \ldots$ Choose a prime number $p>d$ and set $k^{\prime} \equiv\left(p-a_{0}\right) d^{-1} \bmod p^{2}$. Then $a_{k^{\prime}}=a_{0}+k^{\prime} d \equiv p \bmod p^{2}$ and hence, $a_{k^{\prime}}$ can not be a power of a natural number.
Another solution. There can be at most $\lfloor\sqrt{n}\rfloor$ squares in the set $\{1,2, \ldots, n\}$, at most $\lfloor\sqrt[3]{n}\rfloor$ cubes in the same set, etc. The greatest power that can occur in the set $\{1,2, \ldots, n\}$ is $\left\lfloor\log _{2} n\right\rfloor$ and thus there are no more than
$$
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n]{n}\right\rfloor\right.
$$
powers among the numbers $1,2, \ldots, n$. Now we can estimate this sum above:
$$
\begin{aligned}
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n\rfloor\right]{n}\right\rfloor & \leqslant\lfloor\sqrt{n}\rfloor\left(\left\lfloor\log _{2} n\right\rfloor-1\right)< \\
& <\lfloor\sqrt{n}\rfloor \cdot\left\lfloor\log _{2} n\right\rfloor=o(n)
\end{aligned}
$$
This means that every arithmetic progression grows faster than the share of powers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Does there exist an infinite non-constant arithmetic progression, each term of which is of the form $a^{b}$, where $a$ and $b$ are positive integers with $b \geqslant 2$ ?
Answer: no.
|
For an arithmetic progression $a_{1}, a_{2}, \ldots$ with difference $d$ the following holds:
$$
\begin{aligned}
S_{n} & =\frac{1}{a_{1}}+\frac{1}{a_{2}}+\ldots+\frac{1}{a_{n+1}}=\frac{1}{a_{1}}+\frac{1}{a_{1}+d}+\ldots+\frac{1}{a_{1}+n d} \geqslant \\
& \geqslant \frac{1}{m}\left(\frac{1}{1}+\frac{1}{2}+\ldots+\frac{1}{n+1}\right),
\end{aligned}
$$
where $m=\max \left(a_{1}, d\right)$. Therefore $S_{n}$ tends to infinity when $n$ increases.
On the other hand, the sum of reciprocals of the powers of a natural number $x \neq 1$ is
$$
\frac{1}{x^{2}}+\frac{1}{x^{3}}+\ldots=\frac{\frac{1}{x^{2}}}{1-\frac{1}{x}}=\frac{1}{x(x-1)}
$$
Hence, the sum of reciprocals of the terms of the progression required in the problem cannot exceed
$$
\frac{1}{1}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\ldots=1+\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\ldots\right)=2
$$
a contradiction.
Alternative solution. Let $a_{k}=a_{0}+d k, k=0,1, \ldots$ Choose a prime number $p>d$ and set $k^{\prime} \equiv\left(p-a_{0}\right) d^{-1} \bmod p^{2}$. Then $a_{k^{\prime}}=a_{0}+k^{\prime} d \equiv p \bmod p^{2}$ and hence, $a_{k^{\prime}}$ can not be a power of a natural number.
Another solution. There can be at most $\lfloor\sqrt{n}\rfloor$ squares in the set $\{1,2, \ldots, n\}$, at most $\lfloor\sqrt[3]{n}\rfloor$ cubes in the same set, etc. The greatest power that can occur in the set $\{1,2, \ldots, n\}$ is $\left\lfloor\log _{2} n\right\rfloor$ and thus there are no more than
$$
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n]{n}\right\rfloor\right.
$$
powers among the numbers $1,2, \ldots, n$. Now we can estimate this sum above:
$$
\begin{aligned}
\lfloor\sqrt{n}\rfloor+\lfloor\sqrt[3]{n}\rfloor+\ldots+\left\lfloor\left\lfloor\log _{2} \sqrt[n\rfloor\right]{n}\right\rfloor & \leqslant\lfloor\sqrt{n}\rfloor\left(\left\lfloor\log _{2} n\right\rfloor-1\right)< \\
& <\lfloor\sqrt{n}\rfloor \cdot\left\lfloor\log _{2} n\right\rfloor=o(n)
\end{aligned}
$$
This means that every arithmetic progression grows faster than the share of powers.
|
{
"resource_path": "BalticWay/segmented/en-bw02sol.jsonl",
"problem_match": "\n20.",
"solution_match": "\nSolution."
}
|
41e10bd1-b8da-5339-9dda-f468f7533fab
| 605,446
|
Let $\mathbb{Q}_{+}$be the set of positive rational numbers. Find all functions $f: \mathbb{Q}_{+} \rightarrow \mathbb{Q}_{+}$which for all $x \in \mathbb{Q}_{+}$fulfil
(1) $f\left(\frac{1}{x}\right)=f(x)$
(2) $\left(1+\frac{1}{x}\right) f(x)=f(x+1)$
|
Set $g(x)=\frac{f(x)}{f(1)}$. Function $g$ fulfils (1), (2) and $g(1)=1$. First we prove that if $g$ exists then it is unique. We prove that $g$ is uniquely defined on $x=\frac{p}{q}$ by induction on $\max (p, q)$. If $\max (p, q)=1$ then $x=1$ and $g(1)=1$. If $p=q$ then $x=1$ and $g(x)$ is unique. If $p \neq q$ then we can assume (according to (1)) that $p>q$. From (2) we get $g\left(\frac{p}{q}\right)=\left(1+\frac{q}{p-q}\right) g\left(\frac{p-q}{q}\right)$. The induction assumption and $\max (p, q)>\max (p-q, q) \geq 1$ now give that $g\left(\frac{p}{q}\right)$ is unique.
Define the function $g$ by $g\left(\frac{p}{q}\right)=p q$ where $p$ and $q$ are chosen such that $\operatorname{gcd}(p, q)=1$. It is easily seen that $g$ fulfils (1), (2) and $g(1)=1$. All functions fulfilling (1) and (2) are therefore $f\left(\frac{p}{q}\right)=a p q$, where $\operatorname{gcd}(p, q)=1$ and $a \in \mathbb{Q}_{+}$.
|
f\left(\frac{p}{q}\right)=a p q
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{Q}_{+}$be the set of positive rational numbers. Find all functions $f: \mathbb{Q}_{+} \rightarrow \mathbb{Q}_{+}$which for all $x \in \mathbb{Q}_{+}$fulfil
(1) $f\left(\frac{1}{x}\right)=f(x)$
(2) $\left(1+\frac{1}{x}\right) f(x)=f(x+1)$
|
Set $g(x)=\frac{f(x)}{f(1)}$. Function $g$ fulfils (1), (2) and $g(1)=1$. First we prove that if $g$ exists then it is unique. We prove that $g$ is uniquely defined on $x=\frac{p}{q}$ by induction on $\max (p, q)$. If $\max (p, q)=1$ then $x=1$ and $g(1)=1$. If $p=q$ then $x=1$ and $g(x)$ is unique. If $p \neq q$ then we can assume (according to (1)) that $p>q$. From (2) we get $g\left(\frac{p}{q}\right)=\left(1+\frac{q}{p-q}\right) g\left(\frac{p-q}{q}\right)$. The induction assumption and $\max (p, q)>\max (p-q, q) \geq 1$ now give that $g\left(\frac{p}{q}\right)$ is unique.
Define the function $g$ by $g\left(\frac{p}{q}\right)=p q$ where $p$ and $q$ are chosen such that $\operatorname{gcd}(p, q)=1$. It is easily seen that $g$ fulfils (1), (2) and $g(1)=1$. All functions fulfilling (1) and (2) are therefore $f\left(\frac{p}{q}\right)=a p q$, where $\operatorname{gcd}(p, q)=1$ and $a \in \mathbb{Q}_{+}$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
8fabbe4d-28ba-5ce7-bd0e-9e21714aaa57
| 605,454
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
0e5c5fc2-1b05-5f1f-bcc8-f57dac50d8e0
| 605,462
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
As the equation $x_{0} x^{2}+p x+q=0$ has a root $\left(x=x_{0}\right)$, we must have $D \geq 0 \Leftrightarrow p^{2}-4 q x_{0} \geq 0$. (Also the equation $x^{2}+p x+q x_{0}=0$ having the root $x=x_{0}^{2}$ can be considered.)
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
As the equation $x_{0} x^{2}+p x+q=0$ has a root $\left(x=x_{0}\right)$, we must have $D \geq 0 \Leftrightarrow p^{2}-4 q x_{0} \geq 0$. (Also the equation $x^{2}+p x+q x_{0}=0$ having the root $x=x_{0}^{2}$ can be considered.)
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution 2:"
}
|
0e5c5fc2-1b05-5f1f-bcc8-f57dac50d8e0
| 605,462
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
0b386c5a-4a5f-5a5c-b242-a91743be5472
| 605,477
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution 2:"
}
|
0b386c5a-4a5f-5a5c-b242-a91743be5472
| 605,477
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
24d1326e-4bbe-5f14-936f-c49ba46a510c
| 605,500
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution 2:"
}
|
24d1326e-4bbe-5f14-936f-c49ba46a510c
| 605,500
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
9085e1fd-049f-5188-b002-20f2cce73610
| 236,767
|
Let $n \geq 2$ and $d \geq 1$ be integers with $d \mid n$, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$. Prove that there are at least $\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$ choices of $d$ indices $1 \leq i_{1}<i_{2}<\cdots<i_{d} \leq n$ such that $x_{i_{1}}+x_{i_{2}}+\cdots+x_{i_{d}} \geq 0$.
|
Put $m=n / d$ and $[n]=\{1,2, \ldots, n\}$, and consider all partitions $[n]=A_{1} \cup$ $A_{2} \cup \cdots \cup A_{m}$ of $[n]$ into $d$-element subsets $A_{i}, i=1,2, \ldots, m$. The number of such partitions is denoted by $t$. Clearly, there are exactly $\left(\begin{array}{l}n \\ d\end{array}\right) d$-element subsets of $[n]$ each of which occurs in the same number of partitions. Hence, every $A \subseteq[n]$ with $|A|=d$ occurs in exactly $s:=t m /\left(\begin{array}{l}n \\ d\end{array}\right)$ partitions. On the other hand, every partition contains at least one $d$-element set $A$ such that $\sum_{i \in A} x_{i} \geq 0$. Consequently, the total number of sets with this property is at least $t / s=\left(\begin{array}{l}n \\ d\end{array}\right) / m=\frac{d}{n}\left(\begin{array}{l}n \\ d\end{array}\right)=\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$.
|
\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 2$ and $d \geq 1$ be integers with $d \mid n$, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$. Prove that there are at least $\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$ choices of $d$ indices $1 \leq i_{1}<i_{2}<\cdots<i_{d} \leq n$ such that $x_{i_{1}}+x_{i_{2}}+\cdots+x_{i_{d}} \geq 0$.
|
Put $m=n / d$ and $[n]=\{1,2, \ldots, n\}$, and consider all partitions $[n]=A_{1} \cup$ $A_{2} \cup \cdots \cup A_{m}$ of $[n]$ into $d$-element subsets $A_{i}, i=1,2, \ldots, m$. The number of such partitions is denoted by $t$. Clearly, there are exactly $\left(\begin{array}{l}n \\ d\end{array}\right) d$-element subsets of $[n]$ each of which occurs in the same number of partitions. Hence, every $A \subseteq[n]$ with $|A|=d$ occurs in exactly $s:=t m /\left(\begin{array}{l}n \\ d\end{array}\right)$ partitions. On the other hand, every partition contains at least one $d$-element set $A$ such that $\sum_{i \in A} x_{i} \geq 0$. Consequently, the total number of sets with this property is at least $t / s=\left(\begin{array}{l}n \\ d\end{array}\right) / m=\frac{d}{n}\left(\begin{array}{l}n \\ d\end{array}\right)=\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
9629adf8-24b8-5691-bbc3-5831095b9126
| 236,777
|
Let $X$ be a subset of $\{1,2,3, \ldots, 10000\}$ with the following property: If $a, b \in X, a \neq b$, then $a \cdot b \notin X$. What is the maximal number of elements in $X$ ?
Answer: 9901.
|
If $X=\{100,101,102, \ldots, 9999,10000\}$, then for any two selected $a$ and $b, a \neq b$, $a \cdot b \geq 100 \cdot 101>10000$, so $a \cdot b \notin X$. So $X$ may have 9901 elements.
Suppose that $x_{1}<x_{2}<\cdots<x_{k}$ are all elements of $X$ that are less than 100. If there are none of them, no more than 9901 numbers can be in the set $X$. Otherwise, if $x_{1}=1$ no other number can be in the set $X$, so suppose $x_{1}>1$ and consider the pairs
$$
\begin{gathered}
200-x_{1},\left(200-x_{1}\right) \cdot x_{1} \\
200-x_{2},\left(200-x_{2}\right) \cdot x_{2} \\
\vdots \\
200-x_{k},\left(200-x_{k}\right) \cdot x_{k}
\end{gathered}
$$
Clearly $x_{1}<x_{2}<\cdots<x_{k}<100<200-x_{k}<200-x_{k-1}<\cdots<200-x_{2}<$ $200-x_{1}<200<\left(200-x_{1}\right) \cdot x_{1}<\left(200-x_{2}\right) \cdot x_{2}<\cdots<\left(200-x_{k}\right) \cdot x_{k}$. So all numbers in these pairs are different and greater than 100. So at most one from each pair is in the set $X$. Therefore, there are at least $k$ numbers greater than 100 and $99-k$ numbers less than 100 that are not in the set $X$, together at least 99 numbers out of 10000 not being in the set $X$.
|
9901
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $X$ be a subset of $\{1,2,3, \ldots, 10000\}$ with the following property: If $a, b \in X, a \neq b$, then $a \cdot b \notin X$. What is the maximal number of elements in $X$ ?
Answer: 9901.
|
If $X=\{100,101,102, \ldots, 9999,10000\}$, then for any two selected $a$ and $b, a \neq b$, $a \cdot b \geq 100 \cdot 101>10000$, so $a \cdot b \notin X$. So $X$ may have 9901 elements.
Suppose that $x_{1}<x_{2}<\cdots<x_{k}$ are all elements of $X$ that are less than 100. If there are none of them, no more than 9901 numbers can be in the set $X$. Otherwise, if $x_{1}=1$ no other number can be in the set $X$, so suppose $x_{1}>1$ and consider the pairs
$$
\begin{gathered}
200-x_{1},\left(200-x_{1}\right) \cdot x_{1} \\
200-x_{2},\left(200-x_{2}\right) \cdot x_{2} \\
\vdots \\
200-x_{k},\left(200-x_{k}\right) \cdot x_{k}
\end{gathered}
$$
Clearly $x_{1}<x_{2}<\cdots<x_{k}<100<200-x_{k}<200-x_{k-1}<\cdots<200-x_{2}<$ $200-x_{1}<200<\left(200-x_{1}\right) \cdot x_{1}<\left(200-x_{2}\right) \cdot x_{2}<\cdots<\left(200-x_{k}\right) \cdot x_{k}$. So all numbers in these pairs are different and greater than 100. So at most one from each pair is in the set $X$. Therefore, there are at least $k$ numbers greater than 100 and $99-k$ numbers less than 100 that are not in the set $X$, together at least 99 numbers out of 10000 not being in the set $X$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n7.",
"solution_match": "\nSolution:"
}
|
004868eb-7812-5707-961b-5f420804471d
| 605,564
|
There are 2003 pieces of candy on a table. Two players alternately make moves. A move consists of eating one candy or half of the candies on the table (the "lesser half" if there is an odd number of candies); at least one candy must be eaten at each move. The loser is the one who eats the last candy. Which player - the first or the second - has a winning strategy?
Answer: The second.
|
Let us prove inductively that for $2 n$ pieces of candy the first player has a winning strategy. For $n=1$ it is obvious. Suppose it is true for $2 n$ pieces, and let's consider $2 n+2$ pieces. If for $2 n+1$ pieces the second is the winner, then the first eats 1 piece and becomes the second in the game starting with $2 n+1$ pieces. So suppose that for $2 n+1$ pieces the first is the winner. His winning move for $2 n+1$ is not eating 1 piece (according to the inductive assumption). So his winning move is to eat $n$ pieces, leaving the second with $n+1$ pieces, when the second must lose. But the first can leave the second with $n+1$ pieces from the starting position with $2 n+2$ pieces, eating $n+1$ pieces; so $2 n+2$ is a winning position for the first.
Now if there are 2003 pieces of candy on the table, the first must eat either 1 or 1001 candies, leaving an even number of candies on the table. So the second player will be the first player in a game with even number of candies and therefore has a winning strategy.
In general, if there is an odd number $N$ of candies, write $N=2^{m} r+1$, where $r$ is odd. Then the first player wins if $m$ is even, and the second player wins if $m$ is odd: At each move, the player must avoid leaving the other with an even number of candies, so he must eat half of the candies. But this means that the number of candies descend as $2^{m} r+1,2^{m-1} r+1, \ldots, 2 r+1, r+1$, and eventually there is an even number of candies.
|
The second
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
There are 2003 pieces of candy on a table. Two players alternately make moves. A move consists of eating one candy or half of the candies on the table (the "lesser half" if there is an odd number of candies); at least one candy must be eaten at each move. The loser is the one who eats the last candy. Which player - the first or the second - has a winning strategy?
Answer: The second.
|
Let us prove inductively that for $2 n$ pieces of candy the first player has a winning strategy. For $n=1$ it is obvious. Suppose it is true for $2 n$ pieces, and let's consider $2 n+2$ pieces. If for $2 n+1$ pieces the second is the winner, then the first eats 1 piece and becomes the second in the game starting with $2 n+1$ pieces. So suppose that for $2 n+1$ pieces the first is the winner. His winning move for $2 n+1$ is not eating 1 piece (according to the inductive assumption). So his winning move is to eat $n$ pieces, leaving the second with $n+1$ pieces, when the second must lose. But the first can leave the second with $n+1$ pieces from the starting position with $2 n+2$ pieces, eating $n+1$ pieces; so $2 n+2$ is a winning position for the first.
Now if there are 2003 pieces of candy on the table, the first must eat either 1 or 1001 candies, leaving an even number of candies on the table. So the second player will be the first player in a game with even number of candies and therefore has a winning strategy.
In general, if there is an odd number $N$ of candies, write $N=2^{m} r+1$, where $r$ is odd. Then the first player wins if $m$ is even, and the second player wins if $m$ is odd: At each move, the player must avoid leaving the other with an even number of candies, so he must eat half of the candies. But this means that the number of candies descend as $2^{m} r+1,2^{m-1} r+1, \ldots, 2 r+1, r+1$, and eventually there is an even number of candies.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n8.",
"solution_match": "\nSolution:"
}
|
5f6ade93-583f-5247-bd07-cebb4f0f89cb
| 236,799
|
It is known that $n$ is a positive integer, $n \leq 144$. Ten questions of type "Is $n$ smaller than a?" are allowed. Answers are given with a delay: The answer to the $i$ 'th question is given only after the $(i+1)$ 'st question is asked, $i=1,2, \ldots, 9$. The answer to the tenth question is given immediately after it is asked. Find a strategy for identifying $n$.
|
Let the Fibonacci numbers be denoted $F_{0}=1, F_{1}=2, F_{2}=3$ etc. Then $F_{10}=144$. We will prove by induction on $k$ that using $k$ questions subject to the conditions of the problem, it is possible to determine any positive integer $n \leq F_{k}$. First, for $k=0$ it is trivial, since without asking we know that $n=1$. For $k=1$, we simply ask if $n$ is smaller than 2. For $k=2$, we ask if $n$ is smaller than 3 and if $n$ is smaller than 2; from the two answers we can determine $n$.
Now, in general, our first two questions will always be "Is $n$ smaller than $F_{k-1}+1$ ?" and "Is $n$ smaller than $F_{k-2}+1$ ". We then receive the answer to the first question. As long as we receive affirmative answers to the $i-1$ 'st question, the $i+1$ 'st question will be "Is $n$ smaller than $F_{k-(i+1)}+1$ ?". If at any point, say after asking the $j$ 'th question, we receive a negative answer to the $j-1$ 'st question, we then know that $F_{k-(j-1)}+1 \leq n \leq F_{k-(j-2)}$, so $n$ is one of $F_{k-(j-2)}-F_{k-(j-1)}=F_{k-j}$ consecutive integers, and by induction we may determine $n$ using the remaining $k-j$ questions. Otherwise, we receive affirmative answers to all the questions, the last being "Is $n$ smaller than $F_{k-k}+1=2$ ?"; so $n=1$ in that case.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
It is known that $n$ is a positive integer, $n \leq 144$. Ten questions of type "Is $n$ smaller than a?" are allowed. Answers are given with a delay: The answer to the $i$ 'th question is given only after the $(i+1)$ 'st question is asked, $i=1,2, \ldots, 9$. The answer to the tenth question is given immediately after it is asked. Find a strategy for identifying $n$.
|
Let the Fibonacci numbers be denoted $F_{0}=1, F_{1}=2, F_{2}=3$ etc. Then $F_{10}=144$. We will prove by induction on $k$ that using $k$ questions subject to the conditions of the problem, it is possible to determine any positive integer $n \leq F_{k}$. First, for $k=0$ it is trivial, since without asking we know that $n=1$. For $k=1$, we simply ask if $n$ is smaller than 2. For $k=2$, we ask if $n$ is smaller than 3 and if $n$ is smaller than 2; from the two answers we can determine $n$.
Now, in general, our first two questions will always be "Is $n$ smaller than $F_{k-1}+1$ ?" and "Is $n$ smaller than $F_{k-2}+1$ ". We then receive the answer to the first question. As long as we receive affirmative answers to the $i-1$ 'st question, the $i+1$ 'st question will be "Is $n$ smaller than $F_{k-(i+1)}+1$ ?". If at any point, say after asking the $j$ 'th question, we receive a negative answer to the $j-1$ 'st question, we then know that $F_{k-(j-1)}+1 \leq n \leq F_{k-(j-2)}$, so $n$ is one of $F_{k-(j-2)}-F_{k-(j-1)}=F_{k-j}$ consecutive integers, and by induction we may determine $n$ using the remaining $k-j$ questions. Otherwise, we receive affirmative answers to all the questions, the last being "Is $n$ smaller than $F_{k-k}+1=2$ ?"; so $n=1$ in that case.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n9.",
"solution_match": "\nSolution:"
}
|
d1b47dea-833b-5c52-9748-76ceeb99051c
| 236,808
|
A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points $\left(x_{i}, y_{i}\right), i=1,2,3,4$, is the point $\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}\right)$. Let $n$ be the largest natural number with the following property: There are $n$ distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that $n=12$.
|
To prove $n \geq 12$, we have to show that there are 12 lattice points $\left(x_{i}, y_{i}\right)$, $i=1,2, \ldots, 12$, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that $x_{i} \equiv 0(\bmod 4)$ for $i=1, \ldots, 6, x_{i} \equiv 1(\bmod 4)$ for
$i=7, \ldots, 12, y_{i} \equiv 0(\bmod 4)$ for $i=1,2,3,10,11,12, y_{i} \equiv 1(\bmod 4)$ for $i=4, \ldots, 9$.
Now let $P_{i}, i=1,2, \ldots, 13$, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their $x$-coordinates as well as their $y$-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 13 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say $M$ and $M^{\prime}$, such that their midpoint $C$ is a lattice point. Finally, if $M$ and $M^{\prime}$ are the midpoints of $P_{i} P_{j}$ and $P_{k} P_{\ell}$, respectively, $\{i, j, k, \ell\} \subseteq\{1,2, \ldots, 13\}$, then $C$ is the centroid of $P_{i}, P_{j}, P_{k}, P_{\ell}$.
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points $\left(x_{i}, y_{i}\right), i=1,2,3,4$, is the point $\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}\right)$. Let $n$ be the largest natural number with the following property: There are $n$ distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that $n=12$.
|
To prove $n \geq 12$, we have to show that there are 12 lattice points $\left(x_{i}, y_{i}\right)$, $i=1,2, \ldots, 12$, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that $x_{i} \equiv 0(\bmod 4)$ for $i=1, \ldots, 6, x_{i} \equiv 1(\bmod 4)$ for
$i=7, \ldots, 12, y_{i} \equiv 0(\bmod 4)$ for $i=1,2,3,10,11,12, y_{i} \equiv 1(\bmod 4)$ for $i=4, \ldots, 9$.
Now let $P_{i}, i=1,2, \ldots, 13$, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their $x$-coordinates as well as their $y$-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 13 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say $M$ and $M^{\prime}$, such that their midpoint $C$ is a lattice point. Finally, if $M$ and $M^{\prime}$ are the midpoints of $P_{i} P_{j}$ and $P_{k} P_{\ell}$, respectively, $\{i, j, k, \ell\} \subseteq\{1,2, \ldots, 13\}$, then $C$ is the centroid of $P_{i}, P_{j}, P_{k}, P_{\ell}$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n10.",
"solution_match": "\nSolution:"
}
|
13069431-f67f-579e-85a7-7f38c5b537b9
| 605,608
|
Is it possible to select 1000 points in a plane so that at least 6000 distances between two of them are equal?
Answer: Yes.
|
Let's start with configuration of 4 points and 5 distances equal to $d$, like in this figure:
$(\alpha)$
Now take $(\alpha)$ and two copies of it obtainable by parallel shifts along vectors $\vec{a}$ and $\vec{b},|\vec{a}|=|\vec{b}|=d$ and $\angle(\vec{a}, \vec{b})=60^{\circ}$. Vectors $\vec{a}$ and $\vec{b}$ should be chosen so that no two vertices of $(\alpha)$ and of the two copies coincide. We get $3 \cdot 4=12$ points and $3 \cdot 5+12=27$ distances. Proceeding in the same way, we get gradually
- $3 \cdot 12=36$ points and $3 \cdot 27+36=117$ distances;
- $3 \cdot 36=108$ points and $3 \cdot 117+108=459$ distances;
- $3 \cdot 108=324$ points and $3 \cdot 459+324=1701$ distances;
- $3 \cdot 324=972$ points and $3 \cdot 1701+972=6075$ distances.
|
6075
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Is it possible to select 1000 points in a plane so that at least 6000 distances between two of them are equal?
Answer: Yes.
|
Let's start with configuration of 4 points and 5 distances equal to $d$, like in this figure:
$(\alpha)$

Now take $(\alpha)$ and two copies of it obtainable by parallel shifts along vectors $\vec{a}$ and $\vec{b},|\vec{a}|=|\vec{b}|=d$ and $\angle(\vec{a}, \vec{b})=60^{\circ}$. Vectors $\vec{a}$ and $\vec{b}$ should be chosen so that no two vertices of $(\alpha)$ and of the two copies coincide. We get $3 \cdot 4=12$ points and $3 \cdot 5+12=27$ distances. Proceeding in the same way, we get gradually
- $3 \cdot 12=36$ points and $3 \cdot 27+36=117$ distances;
- $3 \cdot 36=108$ points and $3 \cdot 117+108=459$ distances;
- $3 \cdot 108=324$ points and $3 \cdot 459+324=1701$ distances;
- $3 \cdot 324=972$ points and $3 \cdot 1701+972=6075$ distances.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n11.",
"solution_match": "\nSolution:"
}
|
428bb820-9dc4-55d1-bff4-91074290e603
| 236,828
|
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.

|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n12.",
"solution_match": "\nSolution:"
}
|
4ae661df-faa0-5bee-8197-961344b8c4af
| 236,837
|
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.
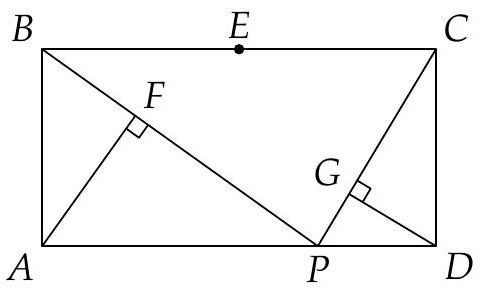
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.

|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n13.",
"solution_match": "\nSolution:"
}
|
619f35fb-87ac-5730-9921-f913e6120328
| 236,848
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.
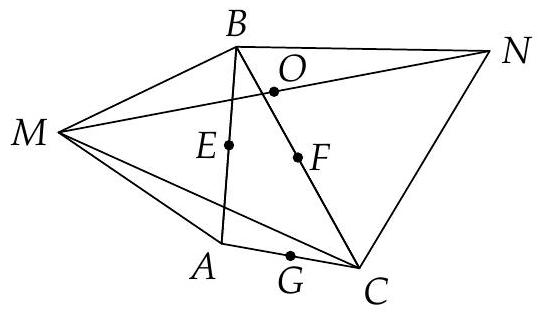
First solution
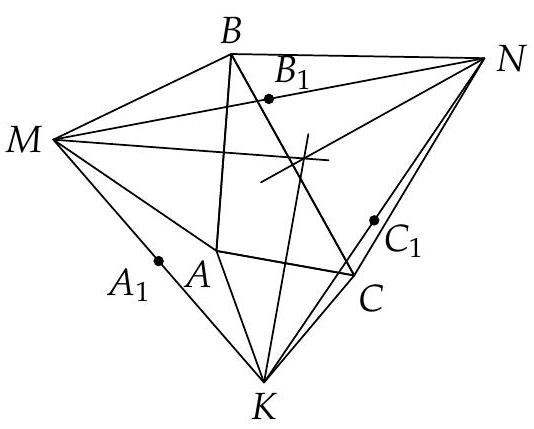
Second solution
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.

First solution

Second solution
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution:"
}
|
0a0ca09c-0909-5242-945c-736209c7b939
| 605,679
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
{
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"problem_match": "\n14.",
"solution_match": "\nSolution 2:"
}
|
0a0ca09c-0909-5242-945c-736209c7b939
| 605,679
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.